Розкладання на множники різниці квадратів двох виразів
Розділ 1. ЦІЛІ ВИРАЗИ
& 16. Розкладання на множники різниці квадратів двох виразів
У тотожності (а – b)(а + b) = а2 – b2 поміняємо місцями ліву і праву частини. Матимемо:
Цю тотожність називають формулою різниці квадратів двох виразів. Читають її так.
Формулу різниці квадратів двох виразів застосовують для розкладання на множники двочлена а2 – b2. Цю формулу можна використовувати і для розкладання на множники різниці квадратів будь-яких двох виразів.
Приклад 1. Розкласти на множники:
1) 16 – х2;
2) 49m4 – 64р6.
Р
2) Оскільки 49m4 = (7m2)2, а 64р6 = (8р3)2, маємо:
49m4 – 64р8 – (7m2)2 – (8р3)2 = (7m2 – 8р3)(7m2 + 8р3).
Приклад 2. Обчислити зручним способом: 1052 – 952.
Р о з в ‘ я з а н н я.
1052 – 952 = (105 – 95)(105 + 95) = 10 ∙ 200 = 2000.
В і д п о в і д ь: 2000.
Приклад 3. Розв’язати рівняння х2 – 25 = 0.
Р о з в ‘ я з а н н я. Оскільки х2 – 25 = (х – 5)(х + 5), маємо:
Х2 – 25 = 0; (х – 5)(х + 5) = 0;
Х – 5 – 0 або х + 5 = 0;
Отже, х = 5 або х = -5.
В і д п о в і д ь: -5; 5.
Запишіть і прочитайте формулу різниці квадратів двох виразів.
521. (Усно)
1) а2 – b2 = (а – b)(а – b);
2) m2 – n2 = (m + n)(m – n);
3) р2 + m2 = (p + q) (р + q);
4) 32 – x2 = (3 – х)(3 + х)?
522. Доберіть замість пропусків такий двочлен, щоб рівність перетворилася на тотожність:
1) x2 – 1 = (x – 1)( … );
2) 4 – р2 = ( … )(2 + р).
523. Доберіть замість пропусків такий вираз, щоб рівність перетворилася на тотожність:
1) m2 – 1 = ( … )(m + 1);
2) 9 – b2 = (3 – b)( … ).
524. (Усно) Розкладіть на множники:
1) а2- 4;
2) 9 – b2;
3) 4х2 – 25m2;
4) х2у2 – 1.
525. Подайте многочлен у вигляді добутку різниці і суми:
1) а2 – 25;
2) 16 – р2;
3) d2 -1,44;
4) 0,09 – m2;
5) b2 – 
;
6) 
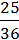– с2.
526. Розкладіть на множники:
1) 36а2 – b2;
2) – а2 + b2;
3) 49×2 – 64;
4) 9m2 – 16n2;
5) -100m2 + 121k2;
6) 0,25 – а2b2;
7) 16m2а2 – 0,01;
8) р2 – с2d2;
9) 81р2m2 – n2.
527. Подайте многочлен у вигляді добутку різниці й суми:
1) а2 – 64;
2) 0,25 – b2;
3) -81 + 36х2;
4) 169р2 – q2;
5) 400а2 – 25m2;
6) 49а2b2 – 16;
7) 900 – а2b2;
8) c2d2 – 4m2;
9) 100а2b2 – 0,16m2.
528. Обчисліть, застосовуючи формулу різниці квадратів:
1) 672 – 572;
2) 432 – 532;
3) 1122 – 882;
4) 21,52 – 21,42;
5) 0,7252 – 0,2752;
6) (5 
)2 – (4 
)2.
529. Обчисліть зручним способом:
1) 432 – 332;
2) 272 – 372;
3) 0,972 – 0,032.
530. Знайдіть значення виразу х2 у2, якщо
1) х = 55; у = 45;
2) х = 2,01; у = 1,99.
531. Розв’яжіть рівняння:
1) х2 – 16 = 0;
2) 
– х2 = 0;
3) у2 – 0,25 = 0;
4) 4х2 – 9 = 0.
532. Знайдіть корені рівняння:
1) х2 – 36 = 0;
2) у2 – 1 = 0;
3) 0,49 – x2 = 0;
4) 64y2 – 49 = 0.
533. Розкладіть на множники:
1) с4 – m6;
2) р8 – а10;
3) а6 – 9m4;
4) 100а6 – 25х8;
5) 0,49 – m4p12;
6) 36x2c14 – 0,16d4;
7) 
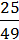А8 – 
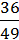B6с2;
8) -0,01m2 + 0,81х6y8;
9)1 
T20a24 – 1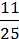 
p16q18.
534. Розкладіть на множники:
1) а8 – 16m8;
2) 36с8 – 49а10;
3) 0,25 – m2а2;
4) -121p8c4 + 4а2;
5) – 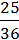а2b4 + 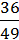C6;
6) 2 
а2b8 – 1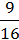 
р6с18.
535. Знайдіть значення виразу:
1) 
;
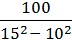2) 
;
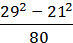3)
.
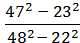536. Подайте вираз у вигляді добутку:
1) (х + 2)2 – 1;
2) 4 – (у + 3)2;
3) (4m – 5)2 – 16;
4) 6,25 – (а – 3,5)2;
5) (2х – 5)2 – 49;
6) 1 – (2х + 1)2.
537. Розкладіть на множники:
1) (р + 2)2 – 9;
2) 16 – (m – 3)2;
3) (3x – 2)2 – 36;
4) х2 – (2х – 1)2;
5) (5а – 3b)2 – 9b2;
6) (3х + 4y)2- 100у2.
538. Знайдіть корені рівняння:
1) (х – 1)2 – 25 = 0;
2) 49 – (2х + 5)2 = 0;
3) (5х + 3)2 = 64;
4) (0,1x – 0,5)2 = 0,36.
539. Розв’яжіть рівняння:
1) (х + 2)2 – 36 = 0;
2) (5x – 4)2- 81 = 0;
3) (2х + 7)2 = 49;
4) (0,2x – 0,5)2 = 0,09.
540. Розкладіть на множники:
1) 16х2 – (1 + 3x)2;
2) (3у – 5)2 – 16у2;
3) 49m2 – (а + 3m)2;
4) (5а – 2b)2- 25а2.
541. Доведіть, що при будь-якому натуральному значенні n значення виразу (n + 7)2 – n2 ділиться на 7.
542. Подайте вираз у вигляді добутку:
1) а6 – (b – 5а3)2;
2) ( 3m2 + 4р)2 – 9m4;
3) (7х + 2y)2- (2х – 7y)2;
4)(а4b + с) – (а + b – с)2;
5) а2(а + 1)2 – с8;
6) (5а – b – 1)2 – (5а + b – 1)2.
543. Розкладіть на множники:
1) (5а2 – 3b)2 – 16а4;
2) mn8 – (3с – 2m4)2;
3) (2а + 3b)2- (4а – 5b);
4) (х – у + t)2- (х – у – t)2.
544. Розв’яжіть рівняння:
1) (3х – 4)2 – (5х – 8)2= 0;
2) х4 – 81 = 0;
3) 16х4 – 1=0;
4) 81х2 + 4 = 0.
545. Доведіть, що різниця квадратів двох послідовних цілих чисел дорівнює сумі цих чисел.
Вправи для повторення
546. Спростіть вираз:
1) (t + 1)(t -7) – (t – 1)(t + 7);
2) (а3 – 2b)(a2 + 2b) – (a2 – 2b)(a3 + 2b).
547. Обчисліть, використовуючи формулу куба двочлена:
1) (100 – 1)3;
2) 413;
3) 293;
4) 0,993.
Цікаві задачі для учнів неледачих
548. Господиня мас важільні терези і гирьку масою 100 г. Як за допомогою чотирьох зважувань відміряти 1,5 кг крупи?
(1 votes, average: 5.00 out of 5)
Loading...