Розміщення. Перестановки. Комбінації
636. 
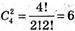
(х, у); (х, z); (х, t); (у, z); (у, t); (z, t).
637.
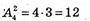
(х, у); (х, z); (х, t); (у, z); (у, t); (z, t);
(у, х); (z, х); (t, х); (z, у); (t, у); (t, z).
638.
ABC, ACB, ВАС, BCA, CAB, СВА P3 =2×3 = 6.
639.
A) 5! = 2 × 3 × 4 × 5 = 120;
Б) 6! = 5! × 6 = 120 × 6 = 720;
В) P4 =2 × 3 × 4 = 24;
Г) P7 = 2 × 3 × 4 × 5 × 6 × 7 = 5040.
640.
Pn – ? | N = 6 | P6 =6! = 2 × 3 × 4 × 5 × 6 = 720; |
N = 7 | P7 =7! = 61 × 7 = 5040; | |
N = 8 | P8 = 8! = 7! × 8 = 40320; | |
N | P9 =9! = 8! × 9 = 362880. |
641.
Першу парту можна заповнити 5-ма способами, a саме
(1, 2); (1, 3); (1, 4); (1, 5); (1, 6), взагалі (n – 1) спосіб, де n – кількість учнів.
Другу парту можна заповнити 3-ма способами,
Взагалі (b – 3) способів, тобто, у даному разі 5×3 = 15 способів.
За третю парту сядуть останні 2 учні.
Враховуючи всі можливі перестановки на кожній парті і самих парт,
Одержуємо 15 × 21 × 21 × 21 × 3! = 6! = 720 способів.
643.
3! = 6 способів.
644.
Перша цифра не може бути 0, тому її можна вибрати 3-ма способами,
Друга цифра – будь-яка (3 способи), третя – 2 способи.
Всього:
645.
A, В, С, D – розміщення по 2.
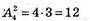
(А, В); (А, С); (A, D); (В, D); (В, С); (С, D);
(В, А); (С, A); (D, A); (D, В); (С, В); (D, С).
646.
П’ять учнів на 10 місцях можна розсадити
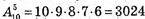
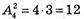
Способами.
647.
А)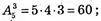 
Б)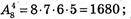 
В)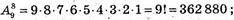 
Г)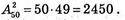 
648.
А)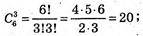 
Б)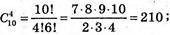 
В)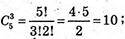 
Г)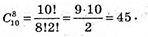 
649.
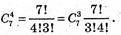
650.
А)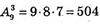 
Б)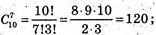 
В)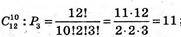 
Г)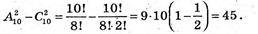 
651
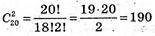Способами.
652.
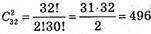Способів.
653.
Якщо з чисельнику число 2, то можна написати 7 правильних дробів:
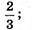
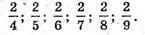
2 → 7 дробів; 3 →6 дробів; 4 → 5 дробів; 5 → 4 дроби;
6 → 3 дроби; 7 → 2 дроби; 8 → 1 дріб.
Усього: 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 дробів.
Відповідь: 28 дробів.
654.
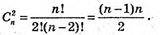
Геометричний спосіб. Кожну з n точок можна з’єднати з (n – 1) точкою.
Всього буде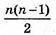 
Відрізків.
655.
Аналогічно з кожної вершини n-кутника можна провести (n – 3) діагоналей.
Всього буде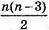 
діагоналей.
N = 10,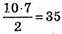 
Діагоналей.
656.
А) двоцифрових чисел буде 5×4 = 20;
Б) трицифрових чисел: 5×4×3 = 60;
В) чотирицифрових чисел: 5×4×З×2 = 120.
657.
Трицифрових чисел: 9×9×8 = 648;
Чотирицифрових чисел: 9×9×8×7 = 4536.
658.
Оскільки кожна цифра числа не менша за 5,
То вибір проводиться з цифр 5, 6, 7, 8, 9.
Трицифрових чисел буде 5×4×3 = 60.
659.
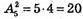словників.
660.
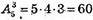способів.
661.
А)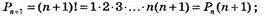 
Б)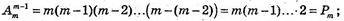 
В)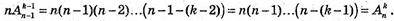 
662.
А) Рn = 42Рn-2, n! = 42×(n – 2)!, (n – 2)!(n – 1)×n = 42×(n – 2)!
N2 – n – 42 = 0n1=7; n2 = -6 n? N, n = 7;
Б) Рn =720Рn-3, n! = 720 × (n – 3)!,
(n – 3)!(n – 2)(n – 1) ×n = 720×(n – 3)!
N(n – 1)(n – 2) = 720,
N(n – 1)(n – 2) = 10 × 9 × 8, n? N, n = 10.
664.
А)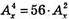 
Х(х – 1)(х – 2)(х – 3) = 56 × (х – 1)
(х – 2)(х – 3) = 56; (х – 2)(х – 3) = 8×7
Х – 2 = 8, х? N, х = 10;
Б)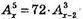 
Х(х – 1)(х – 2)(х – 3) (х – 4) = 72(х – 2)(х – 3)(х – 4)
Х(х – 1) = 72; x(х – 1) = 9 × 8, х? N, х = 9;
В)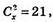 
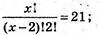
Х(х – 1) = 42 x(x – 1) = 7 × 6, x = 7;
Г)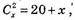 
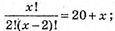
(x – 1)x = 40 +2x
X2- 3x – 40 = 0
X1 = 8, x2 = -5. x? N, x = 8.
665.
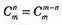За означенням, 
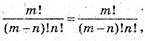очевидна рівність, що треба довести.
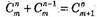за означенням,
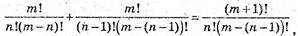
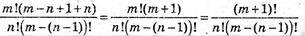Очевидна рівність, що треба довести.
666.
Перший гравець одержує 7 пластинок доміно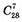 
способом.
Другий –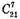 
способом, третій – 
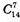способом,
Четвертий – 1 способом.
Усього: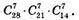 
667.
(1 votes, average: 5.00 out of 5)
Loading...