Розв’язання задач за допомогою рівнянь
79. Нехай Петро купив х зошитів у клітинку, тоді у лінійку він купив (x + 6) зошитів. Усього він купив (х + x + 6) зошитів, або 24 зошити за умовою.
Отже, х + х + 6 = 24; 2х = 24 – 6; 2х = 18; х = 18 : 2; х = 9 зошитів куплено у клітинку; 9 + 6 = 15 зошитів куплено у лінійку. Під повідь: 15 зошитів у лінійку, 9 зошитів у клітинку.
80. Нехай із ‘ другого дерева зібрали х кг вишень, тоді з першого зібрали (х – 12,6) кг вишень. Разом зібрали 65,4 кг вишень.
Отже, х + х – 12,6 = 65,4; 2х = 65,4 + + 12,6; 2х = 78; х = 39 (кг) вишень зібрали з другого дерева; 39 – 12,6 = 26,4 (кг) вишень зібрали з першого дерева.
Відповідь:
81. Нехай х см – менша сторона прямокутника, тоді (х + 1,3) см – більша сторона прямокутника. Його периметр 2(х + х + 1,3) см, або 7,8 см за умовою. Маємо рівняння:
2(х + х + 1,3) = 7,8; 2х + 1,3 = 7,8 : 2; 2х + 1,3 = 3,9; 2х = 3,9 – 1,3; 2х = 2,6; х = 2,6 : 2; х = 1,3 см – довжина меншої сторони; 1,3 + 1,3 = 2,6 (см) – довжина більшої сторони.
Відповідь: 2,6 см; 1,3 см; 2,6 см; 1,3 см.
82. Нехай х см – довжина меншої сторони прямокутника, тоді 11х см – довжина більшої сторони прямокутника. Р = (х + 11х) • 2, а за умовою 144 см.
Отже, (х + 11х) • 2 = 144; 24х = 144; х = 144 : 24; х = 6 см – довжина меншої сторони; 11 • 6 = 66 см – довжина більшої сторони.
Відповідь:
83. Нехай висота Говерли х м, тоді висота Бребенескул (х – 29) м, а Петри – (х – 41) м. Сума їхніх висот дорівнює 6113 м, тому х + (х – 29) + (х – 41) = 6113; х + х – 29 + х – 41 = 6113; 3х – 70 = 6113; 3х = 6113 + 70; 3х = 6183; х = 6183 : 3; х = 2061 (м) – висота Говерли; 2061 – 41 = 2020 (м) – висота Петри; 2061 – 29 = 2032 (м) – висота Бребенескул.
Відповідь: 2061 м, 2020 м, 2032 м.
84. Нехай глибина Каскадної печери х м, тоді глибина Солдатської печери 1,2х м, а глибина Нахімовської печери (х – 26) м. Сума їхніх глибин 1874 м, тому х + 1,2х + х – 26 = 1874; 3,2х = 1874 + 26; 3,2х = 1900; х = 1900 : 3,2; х = 593,75 (м) – глибина Каскадної печери; 593,75 • 1,2 = 712,5 (м) – глибина Солдатської печери; 593,75 – 26 = 567,75 (м) – глибина Нахімовської печери.
Відповідь: 712,5 м; 593,75 м; 567,75 м.
85. Нехай у будинку X однокімнатних квартир, тоді двокімнатних 2х квартир, а трикімнатних (х + 24) квартир. Всього в будинку 160 квартир.
Тому х + 2х + х + 24 = 160; 4х = 160 – 24; 4х = 136; х = 136 : 4; х = 34 – однокімнатних квартир у будинку; 34 • 2 = 68 – двокімнатних квартир у будинку; 34 + 24 = 58 – трикімнатних квартир у будинку.
86. Нехай другий робітник виготовив х деталей, тоді перший робітник виготовив 3х деталей, а третій – (х + 16) деталей. Троє робітників виготовили 96 деталей, тому х + 3х + х + 16 = 96; 5х = 96 – 16; 5х = 80; х = 80 : 5; х = 16 деталей виготовив другий робітник; 16 • 3 = 48 деталей виготовив перший робітник; 16 + 16 = 32 деталі виготовив третій робітник.
Відповідь: 48 деталей, 16 деталей, 32 деталі.
87. Нехай у третьому цеху працює х робітників, тоді у першому цеху працює 4/9х робітників, а в другому цеху – 0,8х робітників. Усього в трьох цехах працює 101 робітник.
Отже,
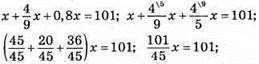
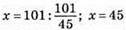 робітників у третьому цеху;
робітників у третьому цеху; 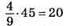 робітників у першому цеху; 0,8 • 45 = 36 робітників у другому цеху.
робітників у першому цеху; 0,8 • 45 = 36 робітників у другому цеху.
88. Нехай за 1-й день велосипедисти проїхали х км, тоді за 2-й день вони проїхали 1,2х км, а за 3-й день 4/5х км. Довжина всього маршруту становить 270 км, тому 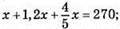 ; х + 1,2х + 0,8х = 270; 3х = 270; х = 270 : 3; х = 90 (км) проїхали велосипедисти за 1-й день;
; х + 1,2х + 0,8х = 270; 3х = 270; х = 270 : 3; х = 90 (км) проїхали велосипедисти за 1-й день;
1,2 • 90 = 108 (км) проїхали велосипедисти за 2-й день;
4/5 • 90 = 72 (км) проїхали велосипедисти за 3-й день.
89. Нехай у кожному маленькому ящику було х кг яблук, тоді у кожному великому (х + 6) кг яблук. У 6 великих було 6(x + 6) кг яблук, а у 8 маленьких було 8x кг яблук. Всього було 232 кг яблук, тому 6(х + 6) + 8x = 232; 6x + 36 + 8x = 232; 14x = 232 – 36; 14x = 196; x = 196 : 14; x = 14 кг яблук було у кожному маленькому ящику; 14 + 6 = 20 кг яблук було у кожному великому ящику.
90. Нехай у кожному ряді другого залу x місць, тоді у кожному ряді першого залу (x + 4) місць. У першому залі всього 12(x + 4) місць, а у другому залі всього 15x місць. Всього у двох залах 534 місця, тому
12(x + 4) + 15x = 534; 12x + 48 + 15x = 534; 27x = 486; x = 18 місць у кожному ряді другого залу; 18 + 4 = 22 місця у кожному ряді першого залу; 18 • 15 = 270 місць у другому залі; 22 • 12 = 264 місця у першому залі.
91. Нехай швидкість велосипедиста х км/год, тоді швидкість мотоцикліста (x + 48) км/год. Відстань між містами 0,8(x + 48) км, або 4x км. Маємо рівняння: 4x = 0,8(x + 48); 4x = 0,8x + 38,4; 3,2x = 38,4; x = 38,4 : 3,2; х = 12 км/год – швидкість велосипедиста; 12 + 48 = 60 км/год – швидкість мотоцикліста.
92. Нехай 1 кг цукерок другого виду коштує x грн., тоді 1 кг цукерок першого виду коштує (x + 12) грн. За цукерки другого виду заплатили 3,5x грн., а за цукерки першого виду – 2(x + 12) грн. За умовою задачі за цукерки заплатили однакову кількість грошей, тому
3,5X = 2(X + 12); 3,5x = 2x + 24; 3,5x – 2x = 24; 1,5x = 24; x = 24 : 1,5; x = 16 грн. коштує 1 кг цукерок другого виду;
16 + 12 = 28 грн. коштує 1 кг цукерок першого виду.
93. Нехай 1 кг огірків коштує л грн., тоді 1 кг помідорів коштує (x + 0,8) грн. За 3,2 кг помідорів заплатили 3,2(x + 0,8) грн., а за 3,6 кг огірків 3,6x грн.
Маємо рівняння:
3,6x = 3,2(x + 0,8); 3,6x = 3,2x + 2,56; 3,6x – 3,2x = 2,56; 0,4x = 2,56; x = 2,56 : 0,4; x = 6,4 (грн.) коштує 1 кг огірків;
6,4 + 0,8 = 7,2 грн. коштує 1 кг помідорів.
Відповідь: 7,2 грн.
94. Нехай у другому баку було x л води, тоді в першому баку було 3x л води. Коли в 1-й бак долили 16 л води, в ньому стало (3x + 16) л води, а в 2-й бак долили 80 л води, в ньому стало (x + 80) л води. Води в баках стало порівну, тому
3x + 16 = х + 80; 3x – х = 80 – 16; 2x = 64; x = 64 : 2; x = 32 (л) води було у другому баку; 32 • 3 = 96 (л) води було в першому баку.
95. Нехай на другій полиці було х книг, тоді на першій полиці було 4x книг. Коли з першої полиці взяли 5 книг, на ній стало (4x – 5) книг. Коли на другу полицю поставили 16 книг, на ній стало (x + 16) книг. Книг на полицях стало порівну, тому 4x – 5 = x + 16; 4x – x = 16 + 5; 3x = 21; x = 21 : 3; x = 7 книг було на другій полиці; 7 • 4 = 28 книг було на першій полиці.
96. Нехай через x років батько буде старше за сина в 5 разів. Тоді батькові буде (26 + x) років, а синові (2 + x) років. Маємо рівняння:
(2 + x) • 5 = 26 + x; 10 + 5x = 26 + x; 5x – x = 26 – 10; 4x = 16; x = 16 : 4; x = 4.
Через 4 роки батько буде старше за сина в 5 разів.
97. Нехай x років тому донька була молодша від матері в 3 рази. Тоді матері було (40 – x) років, доньці (18 – x) років. Маємо рівняння:
40 – x = 3 • (18 – x); 40 – x= 54 – 3x; 3x – x = 54 – 40; 2x = 14; x = 7 років тому доньку була в 3 рази молодша від матері.
98. Нехай орфографічних словників було x, тоді тлумачних було (40 – x). За орфографічні словники заплатили 15x грн., а за тлумачні – 24(40 – x) грн. За все разом заплатили 690 грн.
Тому: 15x + 24(40 – x) = 690; 15x + 960 – 24x = 690; 15x – 24x = 690 – 960; -9x = -270; x = -270 : (-9); x = 30 орфографічних словників було куплено;
40 – 30 = 10 тлумачних словників було куплено.
99. Нехай на перший рахунок вкладник поклав х грн., тоді на другий – (3000 – х) грн. Прибуток на першому рахунку склав 0,07X: грн., а на другому – 0,08(3000 – х) грн. Весь прибуток 222 грн.
Отже, 0,07X + 0,08(3000 – х) = 222; 0,07X + 240 – 0,08х = 222; -0,01х = 222 – 240; -0,01X = -18; х = 1800 грн. вкладник поклав на перший (7 %) рахунок;
3000 – 1800 = 1200 грн. вкладник поклав на другий (8 %) рахунок.
100. Нехай купюр по 2 грн. було х шт., тоді купюр по 5 грн. було (19 – х). В касі було 62 грн.
Отже, 2X + 5(19 – x) = 62; 2х + 95 – 5х = 62; 2х – 5х = 62 – 95; -3х = -33; х = -33 : (-3); х = 11 купюр по 2 грн. було в касі; 19 – 11 = 8 купюр по 5 грн. було в касі.
101. Нехай у сховищах було по х т вугілля. Коли з першого вивезли 680 т, а з другого 200 т вугілля, то у першому сховищі стало (х – 680) т вугілля, а у другому (х – 200) т вугілля. В першому залишилося в 5 разів менше вугілля, ніж у другому, тому 5(х – 680) = х – 200; 5х – 3400 = х – 200; 5х – х = 3400 – 200; 4х = 3200; х = 3200 : 4; х = 800 т вугілля було у кожному зі сховищ спочатку.
102. Нехай у Петра і Василя було по х грн. Після покупки книг у Петра стало (х – 30) грн., а у Василя (х – 45) грн. У Петра залишилось у 2 рази більше грошей, ніж у Василя.
Тому х – 30 = 2(х – 45); х – 30 = 2х – 90; х – 2х = -90 + 30; – х = -60; х = 60 грн. було у кожного хлопця спочатку.
103. Нехай у другому мішку було х кг борошна, тоді у першому 5х кг борошна; Коли з першого у другий пересипали 12 кг борошна, то у першому мішку стало (5х – 12) кг, а у другому (х + 12) кг борошна. Маса борошна в другому мішку склала 5/7 маси борошна в першому мішку. Тому х + 12 = 5/7(5х – 12); 7х + 84 = 5(5х – 12); 7х + 84 = 25х – 60; 7х – 25х = -60 – 84; -18х = -144; х = -144 : (-18); х = 8 кг борошна було у другому мішку.
8 • 5 = 40 кг борошна було у першому мішку.
104. Нехай у другому контейнері було х кг вугілля, тоді у першому контейнері було 3х кг вугілля. Коли з першого у другий пересипали 300 кг вугілля, то у першому контейнері стало (3х – 300) кг, а у другому (х + 300) кг вугілля. Маса вугілля в першому контейнері склала 60 % маси вугілля в другому контейнері, тобто:
3х – 300 = 0,6(х + 300); 3х – 300 = 0,6х + 180; 3х – 0,6х = 180 + 300; 2,4х = 480; х = 480 : 2,4; х = 200 кг вугілля було у другому контейнері.
200 • 3 = 600 кг вугілля було у першому контейнері.
Відповідь: 600 кг, 200 кг.
105. Нехай через x днів першому робітникові залишиться виготовити вдвічі більше деталей, ніж другому. Тоді за х днів 1-й робітник виготовить 4х деталей, 2-й робітник – 5х деталей. 1-му робітникові залишиться виготовити (90 – 4х) деталей, 2-му робітникові – (60 – 5х) деталей. За умовою задачі 1-му робітникові залишилося виготовити вдвічі більше деталей, тому 90 – 4х = 2(60 – 5х); 90 – 4х = 120 – 10х; -4х + 10х = 120 – 90; 6х = 30; х = 30 : 6; х = 5.
Відповідь: через 5 днів першому робітникові залишиться виготовити вдвічі більше деталей.
106. Нехай з першої цистерни використали X л води, тоді з другої цистерни використали 2х л води. В І цистерні залишилося (200 – х) л води, в II цистерні (640 – 2х) л води. За умовою задачі в II цистерні залишилося в 3,5 рази більше води, ніж у першій, тому:
640 – 2х = 3,5(200 – х); 640 – 2х = 700 – 3,5х; -2х + 3,5х = 700 – 640; 1,5х = 60; х = 60 : 1,5; х = 40 л води використали з І цистерни.
40 • 2 = 80 л води використали з II цистерни.
107. Нехай до зустрічі вантажний автомобіль їхав х год, тоді легковий автомобіль – (х + 4) год. Вантажний автомобіль проїхав 50х км, а легковий – 80(х + 4) км. Разом вони проїхали 385 км. Тому 80(х + 4) + 50х = 385; 80х + 320 + 50х = 385; 130х = 385 – 320; 130х = 65; х = 0,5 год проїхав до зустрічі вантажний автомобіль.
0,5 + 4 = 4,5 год проїхав до зустрічі легковий автомобіль.
108. Нехай через x год після виїзду велосипедист зустрівся з пішоходом. Тоді пішохід до зустрічі пройшов (4 • 1,5 + 4х) км, а велосипедист проїхав 16x км. Разом вони подолали 14 км.
Тому 4 • 1,5 + 4х + 16x = 14; 6 + 20х = 14; 20x = 14 – 6; 20x = 8; x = 8/20; x = 2/5 год був у дорозі велосипедист.
2/5 год = 2/5 • 60 = 24 хв.
Відповідь: 24 хв.
109. Нехай швидкість теплохода х км/год, тоді швидкість автобуса (х + 30) км/год. За 6 годин теплохід пройде 6x км, а за 3 год 30 хв = 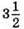 год автобус пройде
год автобус пройде 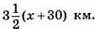 Відстань між містами річкою на 55 км менша, ніж по шосе, тому
Відстань між містами річкою на 55 км менша, ніж по шосе, тому 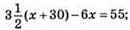 3,5x + 105 – 6x = 55; 3,5x – 6x = 55 – 105; -2,5x = -50; x = -50 : (-2,5); x = 20 км/год – швидкість теплохода.
3,5x + 105 – 6x = 55; 3,5x – 6x = 55 – 105; -2,5x = -50; x = -50 : (-2,5); x = 20 км/год – швидкість теплохода.
20 + 30 = 50 км/год – швидкість автобуса.
110. Нехай швидкість теплохода в стоячій воді дорівнює х км/год, тоді швидкість теплохода за течією річки (х + 2,5) км/год, а проти течії річки – (x – 2,5) км/год. За 4 години за течією річки теплохід пройде 4(x + 2,5) км, а за З години проти течії – 3(x – 2,5) км. Шлях за течією річки на 48 км більший, тому 4(x + 2,5) – 3(x – 2,5) = 48; 4х + 10 – 3х + 7,5 = 48; x = 48 – 17,5; х = 30,5(КМ/ГОД) – швидкість теплохода в стоячій воді.
111. Нехай швидкість течії х КМ/ГОД, річки тоді швидкість човна проти течії річки дорівнює (24 – x) км/год. Шлях, пройдений на плоту, дорівнює 5x км, а шлях проти течії – (24 – x) • 1,5 км. Проти течії турист проплив на 23 км більше, тому (24 – x) • 1,5 – 5х = 23; 36 – 1,5x – 5x = 23; -6,5x = 23 – 36; -6,5x = -13; x = -13 : (-6,5); x = 2 км/год – швидкість течії річки.
112. Нехай у першому ящику x кг печива, тоді у другому ящику (55 – x) кг печива. Коли з першого ящика у другий переклали 1/3 маси печива, то в першому ящику стало 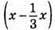 кг печива, а у другому –
кг печива, а у другому – 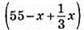 кг печива. В першому ящику стало на 5 кг більше, ніж у другому.
кг печива. В першому ящику стало на 5 кг більше, ніж у другому.
Тому 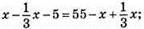
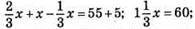
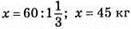 печива було у першому ящику.
печива було у першому ящику.
55 – 45 = 10 кг печива було у другому ящику.
113. Нехай у І ящику було x кг груш, тоді у II ящику (24 – x) кг груш. Коли з І ящика у II ящик переклали 3/7 маси груш, то в І ящику стало 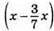 кг, а у II ящику
кг, а у II ящику 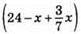 кг. У II ящику груш стало у 2 рази більше, тому
кг. У II ящику груш стало у 2 рази більше, тому 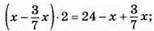
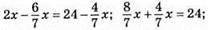
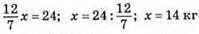 груш було у І ящику.
груш було у І ящику.
24 – 14 = 10 кг груш було у II ящику.
114. Нехай усього було x книжок. Тоді на І полиці стояло – 4/15x книг, на II полиці 0,6x книг, а на III – 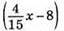 книг. Маємо рівняння:
книг. Маємо рівняння:
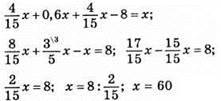 Книг стояло на трьох полицях.
Книг стояло на трьох полицях.
115. Нехай у чотири бідони розлили x л молока. Тоді в перший бідон налили 0,3x л молока, у другий бідон – 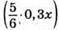 л молока, у третій – (0,3x – 26) л молока, в четвертий –
л молока, у третій – (0,3x – 26) л молока, в четвертий – 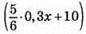 л молока.
л молока.
Маємо рівняння:
0,3х + 5/6 • 0,3х + 0,3х – 26 + 5/6 • 0,3х + 10 = х; 0,3х + 0,25х + 0,3х + 0,25х – х = 26 – 10; 0,1х = 16; х = 160 л молока розлили в чотири бідони.
116. Нехай було х туристів. Тоді наметів було 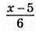 штук, або
штук, або 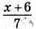 штук.
штук.
Маємо рівняння: 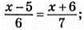 7х – 35 = 6х + 36; 7х – 6х = 36 + 35; х = 71.
7х – 35 = 6х + 36; 7х – 6х = 36 + 35; х = 71.
Відповідь: 71 турист.
117. Нехай було х апельсинів. Тоді учнів у 7 класі було 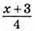 осіб, або
осіб, або 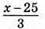 осіб.
осіб.
Маємо рівняння: 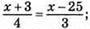 3х + 9 = 4х – 100; 3х – 4х = -100 – 9; – х = -109; х = 109 апельсинів було всього.
3х + 9 = 4х – 100; 3х – 4х = -100 – 9; – х = -109; х = 109 апельсинів було всього.
118. Нехай робітник планував виконати роботу за х днів, тоді він повинен виготовити 20х деталей за планом. Але робітник виготовляв щодня 20 + 8 = 28 деталей і за (х – 2) дні виготовив 28 • (х – 2) деталей, що на 8 деталей більше плану. Отже, 28 (х – 2) – 20х = 8; 28х – 56 – 20х = 8; 8х = 8 + 56; 8х = 64; х = 64 : 8; х = 8 днів за планом необхідно робітникові для виконання плану.
119. Нехай учень планував розв’язати х задач, тоді він мав виконати завдання за x/10 днів. Але він розв’язував щодня 10 + 4 = 14 задач і розв’язав (х – 2) задачі за 3 дні до екзамену за 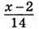 днів.
днів.
Маємо рівняння: 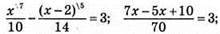 2x + 10 = 210; 2х = 210 – 10; 2х = 200; х = 200 : 2; х = 100 задач планував розв’язати учень.
2x + 10 = 210; 2х = 210 – 10; 2х = 200; х = 200 : 2; х = 100 задач планував розв’язати учень.
120. Нехай у даному двоцифровому числі х одиниць, тоді десятків 3х і число дорівнює 3х • 10 + х. Якщо цифри переставити, то число буде дорівнювати 10х + 3х. Отримане число менше даного на 54, тому 3х • 10 + х – (10х + 3х) = 54; 31х – 13х = 54; 18х = 54; х = 54 : 18; х = 3 – число одиниць; 3 • 3 = 9 – число десятків.
Тоді 93 – шукане число.
121. Нехай х – кількість одиниць, тоді (х – 2) – кількість десятків.
10(х – 2) + х – шукане двоцифрове число.
Якщо цифри числа переставити, то одержимо число 10х + х – 2.
Отримане число більше даного в 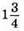 рази, тому
рази, тому 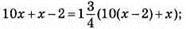
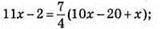
44х – 8 = 7(11х – 20); 44х – 8 = 77х – 140; 44х – 77х = -140 + 8; -33х = -132; х = 4 – кількість одиниць; 4 – 2 = 2 – кількість десятків.
24 – шукане число.
122. Нехай х км/год – швидкість другого автомобіля, тоді (х + 10) км/год – швидкість першого автомобіля. Швидкість зближення автомобілів (х + х + 10) км/год, за 2 години автомобілі зблизяться на 2(х + х + 10) км, а за умовою задачі ця відстань дорівнює (270 – 30) км.
Отже, 2(х + х + 10) = 270 – 30; 2(2х + 10) = 240; 2х + 10 = 120; 2х = 120 – 10; 2х = 110; х = 110 : 2; х = 55 км/год – швидкість другого автомобіля. 55 + 10 = 65 км/год – швидкість першого автомобіля.
123. Нехай першого сплаву треба взяти х кг, тоді другого сплаву (300 – х) кг. У І сплаві 0,09х кг цинку, у II сплаві 0,3(300 – х) кг цинку.
Разом у двох сплавах 0,09х + 0,3(300 – х) кг цинку, або 0,23 • 300 кг.
Отже, 0,09х + 0,3(300 – х) = 0,23 • 300; 0,09х + 90 – 0,3х = 69; -0,21х = 69 – 90; -0,21х = -21; х = 100 кг першого сплаву треба взяти. 300 – 100 = 200 кг другого сплаву треба взяти.
124. Нехай І розчину взяли х кг, тоді II розчину взяли (50 – х) кг. І розчин містить 0,25х кг солі, II – 0,4(50 – х) кг. Всього 0,25х + 0,4(50 – х) кг солі, або 0,34 • 50 кг солі за умовою.
Тому 0,25х + 0,4(50 – х) = 0,34 • 50; 0,25х + 20 – 0,4х = 17; -0,15х = 17 – 20; -0,15х = -3; х = 20 кг І розчину треба взяти. 50 – 20 = 30 кг II розчину треба взяти.
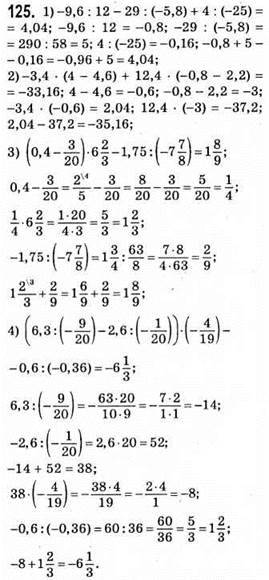
126. 1) Якщо х = 4, то 14 – 6х = 14 – 6 • 4 = 14 – 24 = -10.
Якщо х = -2, то 14 – 6х = 14 – 6 • (-2) = 14 + 12 = 26.
Якщо х = 0, то 14 – 6х = 14 – 6 • 0 = 14.
Якщо х = -0,3, то 14 – 6х = 14 – 6 • (-0,3) = 14 + 1,8 = 15,8.
Якщо х = 3/8, то 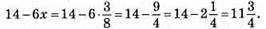
2) Якщо а = 7, а2 + 3 то 72 + 3 = 49 + 3 = 52.
Якщо а = -2, то a2 + 3 = (-2)2 + 3 = 4 + 3 = 7.
Якщо а = 0, то а2 + 3 = 02 + 3 = 3.
Якщо а = 0,4, то а2 + 3 = 0,42 + 3 = 0,16 + 3 = 3,16.
Якщо 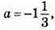 то
то
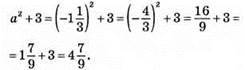
127.
X | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
-3х + 2 | 14 | 11 | 8 | 5 | 2 | -1 | -4 | -7 | -10 |
128. *37* ділиться на 6, тоді воно повинне бути парним (ділитися на 2) і сума цифр повинна ділитися на 3.
2370 | 3372 | 1374 | 2376 | 3378 |
5370 | 6372 | 4374 | 5376 | 6378 |
8370 | 9372 | 7374 | 8376 | 9378 |
Якщо ліворуч і праворуч треба приписати одну і ту саму цифру, то це 4.
4374 ділиться на 6.
129. 1) х2 = 0, х = 0;
2) х2 = -1; немає коренів;
3) |х| = х; коренем є будь-яке невід’ємне число;
4) |х| = – х; коренем є будь-яке недодатне число.
130. 1) 1/x може бути цілим числом, якщо х = ±1, а також х = 1/n, де n – будь-яке ціле число;
2) 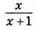 – ціле, якщо х = 0, х = -2.
– ціле, якщо х = 0, х = -2.