Обчислення об’ємів тіл за допомогою інтеграла
1210.
Об’єм призми обчислимо за формулою: V = Sосн. × Н, де H – висота призми.
V = Q × l × sin а.
Відповідь: l sin а.
1211.
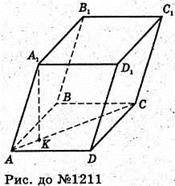
Нехай ABCDA1B1CD1- паралелепіпед.
AB = 6 дм, AD = 8 дм, ∠BAD = 45°, AA= 7 дм, ∠AAK = 45°.
З ΔA1AK: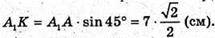 
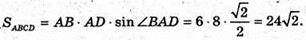
Отже, об’єм V паралелепіпеда дорівнює:
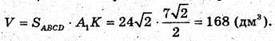
Відповідь: 168 дм3.
1212.
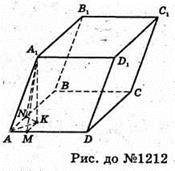
Нехай ABCDA1B1C1D1- заданий паралелепіпед. Проведемо A1K – висоту паралелепіпеда і KM + AD, KN + АВ, тоді за теоремою про три
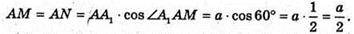
З ΔАKМ: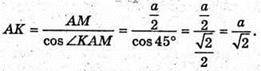 
З ΔA1AK: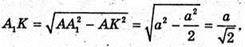 
Отже, об’єм паралелепіпеда дорівнює:
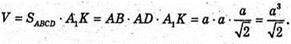
Відповідь: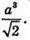 
1213.
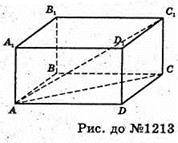
Нехай ABCDA1B1C1D1- паралелепіпед, ABCD – ромб,
AS = BC = CD = DA = 4 см, ∠BAD = 60°. ∠C1AC = 60°.
Знайдемо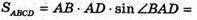 
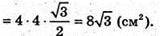
З ΔACD: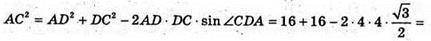 
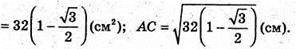
З ΔAC1C: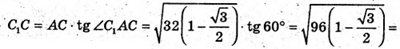 
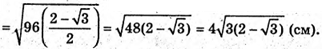
Отже, об’єм V паралелепіпеда:
Відповідь: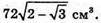
1214.
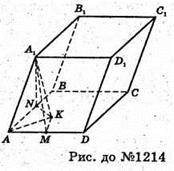
Нехай ABCDA1B1C1D1- заданий паралелепіпед. Проведемо Α1K – висоту паралелепіпеда і KM + AD, KN + AB, тоді за теоремою про три перпендикуляри A1M + AD, A1N + AB. ΔA1AM = ΔA1AN
(AA1- спільна гіпотенуза. ∠A1AM = ΚΑ,ΑΝ),
А отже,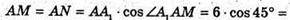 
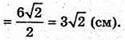
3 ΔAKΜ: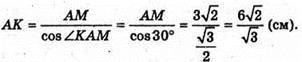 
З ΔΑ1AK: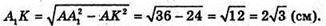 
Отже, об’єм паралелепіпеда дорівнює:
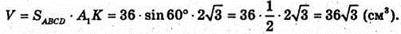
Відповідь: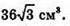 
1215.
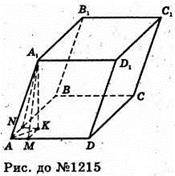
Нехай ABCDA1B1C1D1- заданий паралелепіпед. Проведемо висоту A1K паралелепіпеда і KM + AD, KN + АВ, тоді за теоремою про три перпендикуляри A1M + AD, A1N + АВ. ΔAA1M = ΔAA1N (AA1- спільна гіпотенуза,
∠A1AM = ∠A1AN = 60°), отже,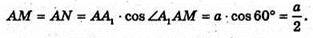 
Далі з ΔАKМ: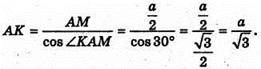 
З ΔA1AK: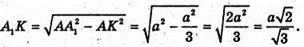 
Об’єм паралелепіпеда
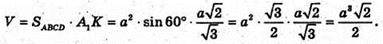
1216.
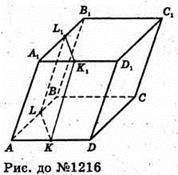
Нехай LL1K1K – переріз похилого паралелепіпеда ABCDA1B1C1D1.
(LL1K1K) ? A1A. AL = LB, AK = KD. S1площа ΔALK,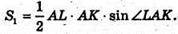 
S2- площа ABCD, S2= 2AL × 2АK × sin∠LAK. S3- площа LBCDK.
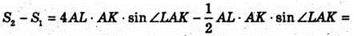
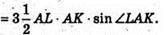
Знайдемо відношення V1- призми ALKA1L1K1 і V2- призми LBCDKL1B1C1D1K1.
Відповідь: 1 : 7.
1217.
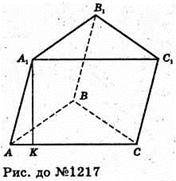
Нехай ABCA1B1C1- призма, AB = BC = AC = a, (AA1C1C) + (ABC).
Проведемо AK + AC – висоту призми. ∠A1AK = α. AA1C1C – ромб, AA1= АС.
З ΔA1AK: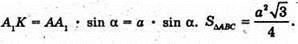 
Отже,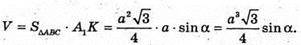 
Підставимо дані а = 17 см, α = 65°, отримаємо:
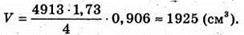
Відповідь: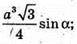 
1925 см3.
1218.
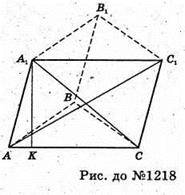
Нехай (AA1C1C) + (ABC), AB = BC = CA = а. AA1C1C — ромб, AA1 = AC = a,
A1C = b. За властивістю діагоналей паралелограма маємо:
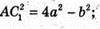
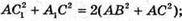
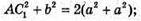
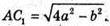
Знайдемо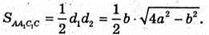 
З другого боку SA1AC1C = AC × A1K = а × A1K.
Прирівняємо праві частини: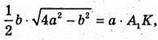 
Звідси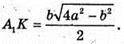 
Отже, об’єм паралелепіпеда дорівнює:
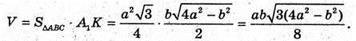
Відповідь: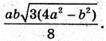 
1219.
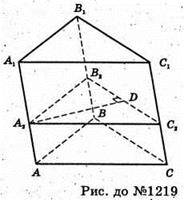
Нехай площа грані BB1C1C дорівнює Q.
Проведемо площину A2B2C2, яка перпендикулярна бічним ребрам, тоді A2D = m. Знайдемо площу перпендикулярного перерізу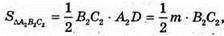 
і тоді для шуканого об’єму маємо: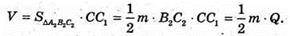 
Відповідь: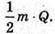 
1220.
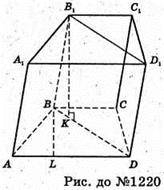
Нехай в призмі ABCDA1B1C1D1 ABCD – трапеція, AD = 44 см, BC – 28 см,
AB = CD= 17 см. (B1D1DB) + (ABCD), ∠B1BK = 45°.
Розглянемо трапецію ABCD: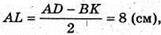 
LD = 36 см.
3ΔABL: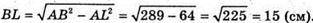 
3ΔBLD: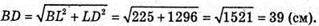 
B1D1DB – ромб, отже, B1B = 39 см. Проведемо B1K + BD.
3 ΔB1BK: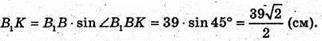 
Отже, об’єм призми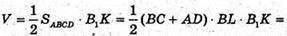 
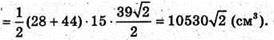
Відповідь: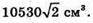 
1221.
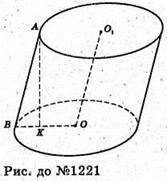
Нехай OB – радіус основи похилого Циліндра, OB = 12 см, AB = 23 см.
Проведемо AK + BO, ∠ ABK = 72°.
З ΔABK: AK = AB sin 72° = 23 × sin 72°.
Отже, V циліндра дорівнює:
V = π × OB2× ΑK = π × 144 × 23 × sin 72° ≈ 9880 (см3).
Відповідь: ≈ 9880 см3.
1222.
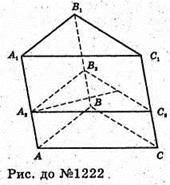
Нехай ABCA1B1C1- задана призма, AA1 = BB1 = CC1 = 8 см, A2B2 = 13 см,
B2C2 = 14 см, C2A2 = 15 см. Оскільки A2B2, B2C2 і C2A2- відстані між бічними ребрами, отже, A2B2 + A1A і A2B2 + B1B, B2C2Δ B1B і B2C2 + C1C, A2C2 + A1A
І A2C2+ C1C1 отже, A2B2C2- переріз.
Знайдемо площу AA2B2C2за формулою Герона:
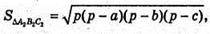
Де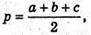 
а а, b, с – сторони трикутника;
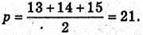
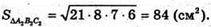
Отже, V призми дорівнює: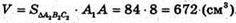 
Відповідь: 672 см3.
1223.
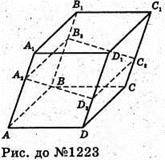
Ехай SA1ADD1 =21 см2, SA1ABB1=49 см2. AA1 = 7 см.
A2B2C2B2- переріз, A2D2+ AA1, A2B2+ AA1.
SA1ABB1= A1A × A2B2, 49 = 7 × A2B2, звідси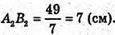 
SA1ADD1 = A1A × A2D2, 21 = 7 × A2B2, звідси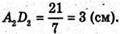 
Знайдемо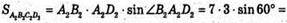 
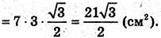
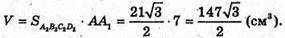
Відповідь: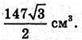 
1224.
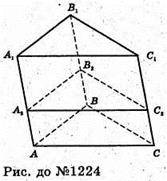
Нехай (A1ABB1) + (B1BCC1). B1B = 10 см, A2B2 = 5 см, B2C2 = 12 см.
A2B2C2- перпендикулярний переріз. ΔA2B2C2- прямокутний (∠B2= 90°).
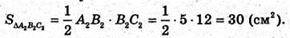
Знайдемо об’єм призми: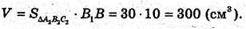 
Відповідь: 300 см3.
1225.
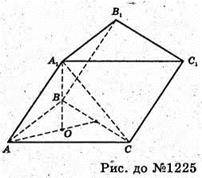
Нехай в призмі ABCA1B1C1 ABC – правильний трикутник.
AB = BC = AC = a, A1A = A1B = A1C.
Знайдемо AO – радіус описаного кола навколо ΔABC: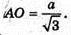 
З ΔAA1O: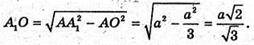 
Об’єм V призми дорівнює: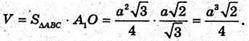 
Відповідь: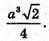 
1226.
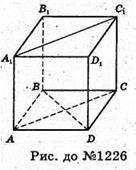
Нехай ABCDA1B1C1D1- паралелепіпед, ABCD – паралелограм,
AB = 6 см, BC = 14 см, BD = 12 см.
За властивістю діагоналей паралелограма маємо:
BD2 + AC2 = = 2(АВ2 + BC2); 144 + AC2 = 2(36 + 196); 144 + AC2 = 464;
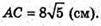AC2 = 464 – 144 = 320;
SA1ACD1 = AA × АС,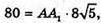 
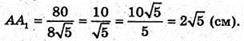
Знайдемо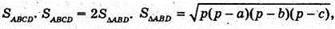
Де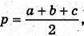 
а, b, с – сторони ААВС.
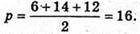
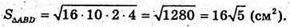
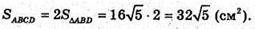
Знайдемо V призми: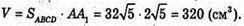 
Відповідь: 320 см3.
1227.
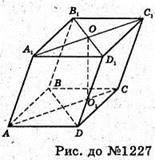
Нехай ABCDA1B1C1D1- похилий паралелепіпед, AC = 10 см, B1D1 = 8 см.
Оскільки кутом між мимобіжними прямими є кут між прямими, які перетинаються і паралельні даним мимобіжним прямим, отже,
BD? B1D1, AC? A1C1, то ∠COD = 30°.
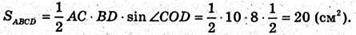
Проведемо OO1Δ (ABCD), OO1 = 5 см.
Об’єм паралелепіпеда V = SABCD × OO1 = 20 × 5 = 100 (см3).
Відповідь: 100 см3.
1228.
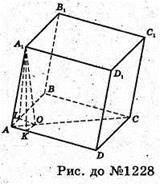
Нехай ABCDA1B1C1D1- паралелепіпед, AB = а, AD = b, AA1 = c,
∠A1AK = α, ∠A1AL = α. ΔA1AK = ΔA1AL, звідси AK = AL = AA1× cos α = с × cos α. ΔAOK = ΔAOL, звідси ∠OAK = ∠OAL = 45°.
З ΔAOK: OK = AK × tg∠OAK = c × cosα × tg45° = c × cos α.
З ΔAA1K: A1K = AA1× sin α = с × sin × α.
3 ΔAOK: OK = AK × tg ∠OAK = с × cos α × tg 45° = c cos α.
3 ΔA1OK: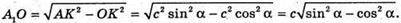 
Отже, об’єм паралелепіпеда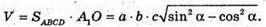 
Відповідь: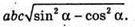 
1229.
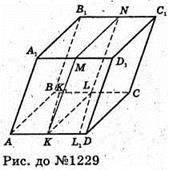
Нехай ABCDA1B1C1D1- паралелепіпед. Розділимо сторони основи на відрізки AK, KD і BL, LC, так що AK = a, KD = b, BL = b, LC = c.
З’єднаємо точки K I L. Отримаємо дві трапеції ABLK і LKDC.
Нехай H – висота паралелепіпеда.
Проведемо K1K + AD1, LL1 + AD, K1K = LL1.
Позначимо K1K = LL1 = h.
Знайдемо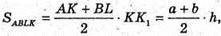 
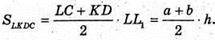
Об’єм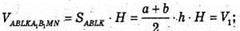 
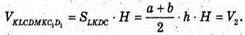
Отже, V1 = V2, KMNL – шуканий переріз.
1230.
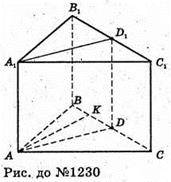
Проведемо в призмі ABCA1B1C1переріз AA1D1D.
Точка D ділить сторону основи на відрізки BD = а, DC = а.
Нехай AA1 = H.
Проведемо в AABD і AADC висоту AK, вона спільна для обох трикутників, нехай AK = h.
Тоді отримаємо V 1 = SABD × AA1, V 2 = SADC × AA1,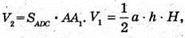 
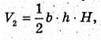
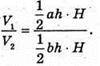
З другої сторони V1: V2 = 1 : 2. Отже, маємо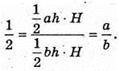 
Звідси можна зробити висновок, що січна площина проходить через точку, яка ділить сторону основи, протилежну ребру призми у відношенні 1 : 2.
1231.
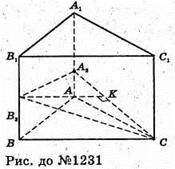
ABCA1B1C1- похила призма, AC = 8 см, BB1 = 6 см.
Оскільки кут між AC і BB1дорівнює 60°, то кут між AC і AA1дорівнює 60°.
Через точку C проведемо площину, перпендикулярну до бічних ребер призми, отримаємо перпендикулярний переріз CB2A2. В трикутнику B2A2C проведемо висоту B2K (B2K + A2C), тоді B2K = 5 см.
Iз ΔAA2C: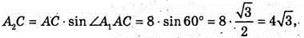 
Тоді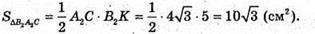 
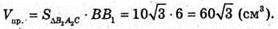
Відповідь: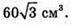 
1232.
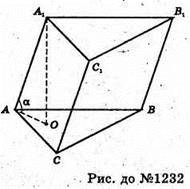
Нехай ABCA1B1C1- дана призма, Sосн. = S, AA1 = l.
Проведемо A1O + (ABC), тоді V = Sосн. × H = S × H.
Із ΔAA1O маємо A1O = AA1 × sin ∠A1AO = l sin φ.
Тоді V = S × A1O = Sl sin φ.
Оскільки S i l задані числа, то V буде мати найбільше значення, якщо sin φ буде найбільшим. Оскільки sin φ = 1, якщо φ = 90°, то тоді AA1+ (ABC).
Таким чином, із всіх призм, які мають одну й ту саму основу і бічне ребро, найбільший об’єм має пряма призма, що й треба було довести.
1233.
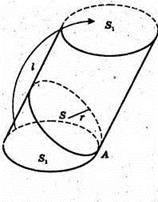
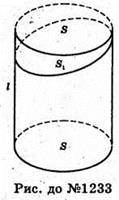
Нехай задано похилий циліндр з основою S1(еліпс) і твірною l. Через точку А проведемо площину, яка перпендикулярна до твірної і перетинає циліндр по кругу радіуса г, тоді площа цього круга S = πr2. Ту частину циліндра, яка лежить нижче цієї площини, перенесемо на верхню основу похилого циліндра. В результаті отримаємо прямий циліндр з основою S і висотою l. Оскільки об’єми цих циліндрів рівні, то V = Sl = πr2l.
Відповідь: πr2l.
1234.
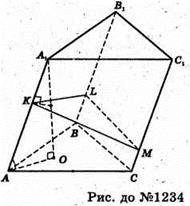
Нехай ABCA1B1C1- похила призма, площа основи якої S1, а бічне ребро дорівнює l, A1O + (ABC), ∠A1AO = φ, тоді об’єм призми дорівнює V = S1× l sin φ. Проведемо перпендикулярний переріз KLM, площа якого дорівнює S, тоді об’єм призмі V= Sl.
Отже, маємо S1l sin φ = SI, тоді S1 sin φ = S. Якщо бічне ребро нахилене до площини основи під кутом φ, то кут між площиною основи і площиною перпендикулярного перерізу дорівнює куту між перпендикулярами до цих площин, тобто між прямими KA1 і AO, тобто α = 90° – φ, тоді φ = 90° – α, тоді
S1sin(90° – α) = S або S1 cos α = S.
Отже, площа проекції многокутника дорівнює площі многокутника помноженій на косинус кута між площиною проекції і площиною многокутника.
1235.
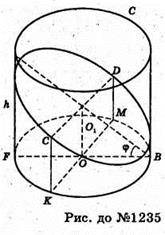
Нехай задано еліпс з осями AB = 2b, CD = 2а, який лежить на поверхні циліндра, діаметр якого KM, KM = CD = 2а, a висота циліндра дорівнює h. Знайдемо об’єм циліндра V = πa2h. (І)
З іншого боку V = Sел. × cos φ × h, де φ – кут між площиною еліпса і площиною основи циліндра.
Із трикутника O1BO маємо: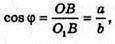 
Тоді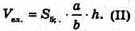 
Прирівнюючи (І) і (II), одержуємо: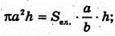 
Тоді Sел. = πab.
Відповідь: πab.
(1 votes, average: 5.00 out of 5)
Loading...