Розв’язування текстових задач за допомогою рівнянь
Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ
§ 13. Розв’язування текстових задач за допомогою рівнянь
Розглянемо текстові задачі, одним із способів розв’язування яких є складання рівнянь.
Задача 1. У садку росли яблуні й вишні – всього 32 дерева, причому яблунь було на 4 більше, ніж вишень. Скільки яблунь і скільки вишень росло в садку?
Розв’язання. Нехай у садку росло х вишень, тоді яблунь було х + 4. Оскільки всього дерев було 32, то отримаємо рівняння х + х + 4 = 32.
Спрощуємо вираз х + х = 1 ∙ х + 1 ∙ х =
Маємо: 2х + 4 = 32.
2х – невідомий доданок. Щоб його знайти, треба від 32 відняти 4. Отже, 2х = 32 – 4, 2х = 28, х = 28 : 2; х = 14. У садку росло 14 вишень, тоді яблунь було 14 + 4 = 18.
Задача 2. За зміну майстер виточив утричі більше деталей, ніж учень. Скільки деталей виточив за зміну учень, якщо ця кількість на 18 менша, ніж кількість деталей, що виточив майстер?
Розв’язання. Нехай учень виточив х деталей, тоді майстер, що виточив утричі більше, – 3х деталей. Оскільки 3х більше за х на 18, то отримуємо рівняння 3х – х = 18. Оскільки 3х – х = 3х – 1х = х(3 – 1) = х ∙ 2 = 2х, то маємо 2х = 18, х = 18 : 2, х = 9. Отже, учень виточив
Достатній рівень
453. Сергій за два дні прочитав 78 сторінок, причому за другий день він прочитав удвічі більше, ніж за перший. Скільки сторінок прочитав Сергій за перший день?
454. Сума двох чисел дорівнює 195. Знайди ці числа, якщо одне з них у 4 рази більше, ніж інше.
455. В автопарку вантажних автомобілів у 5 разів більше, ніж легкових. Скільки в автопарку легкових автомобілів, якщо їх на 52 менше, ніж вантажних?
456. Микола мав на 4 грн. 71 коп. більше, ніж Степан. Скільки грошей мав Степан, якщо їх у 4 рази менше, ніж у Миколи?
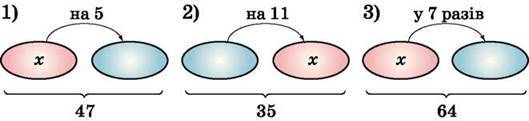
457. Склади рівняння до задач за рисунками. Стрілка спрямована у бік більшого числа. Розв’яжи рівняння.
458. Баба Яга зібрала на 3 мухомори більше, ніж Чахлик Невмирущий. Скільки мухоморів зібрав кожний з них, якщо разом вони зібрали 75 мухоморів?
459. У першому бідоні молока на 7 л більше, ніж у другому. Скільки літрів молока в кожному бідоні, якщо в двох бідонах разом 53 л?
Високий рівень
460. Три кухарки разом зліпили 233 вареники з вишнями. Причому друга кухарка зліпила на 6 вареників більше, ніж перша, третя – на 11 вареників більше, ніж перша. Скільки вареників зліпила кожна кухарка?
461. За три дні було зібрано 1420 кг картоплі. Причому за другий день зібрали вдвічі більше, ніж за перший, а за третій – на 220 кг більше, ніж за перший. Скільки кілограмів картоплі збирали кожного дня?
462. Блокнот, зошит і ручка разом коштують 8 грн. 25 коп. Ручка утричі дорожча за зошит, а зошит на 75 коп. дешевший від блокнота. Скільки коштують зошит, блокнот і ручка окремо?
Вправи для повторення
463. Не обчислюючи, порівняй добутки (<, >, =):
1) 152 ∙ 7 і 152 ∙ 8; 2) 471 ∙ 11 і 473 ∙ 11;
3) 212 ∙ 32 і 211 ∙ 30; 4) 329 ∙ 12 і 12 ∙ 329.
464. Спрости вираз і знайди його значення:
1) 7х ∙ 20у, якщо х = 5, у = 17;
2) 125а ∙ 8b ∙ 7с, якщо a = 2, b = 3, c = 1.
465. Розв’яжи рівняння:
1) 2у + 3у – 7 = 33; 2) 7х – х + 4 = 40.
Домашня самостійна робота № 3
1. Учень планував за канікули розв’язати 20 задач. За перший день він розв’язав а задач. Скільки задач залишилося розв’язати учневі?
А) 20а; Б) а – 20; В) 20 – а; Г) 20 + а.
2. Коренем якого з рівнянь є число 8?
A) 20 – х = 11; Б) 7х = 56;
B) х + 19 = 30; Г) 36 : х = 4.
3. Власна швидкість катера дорівнює 20 км/год, а швидкість течії дорівнює 2 км/год. Яка швидкість катера за течією?
A) 18 км/год; Б) 19 км/год;
B) 22 км/год; Г) 24 км/год.
4. Обчисли значення у за формулою у = 5х – 3, якщо х = 7.
А) 32; Б) 38; В) 35; Г) 9.
5. Розв’яжи рівняння 972 : х = 27.
А) 945; Б) 34; В) 26244; Г) 36.
6. Від двох пристаней, відстань між якими 108 км, одночасно вийшли назустріч один одному два катери. Перший катер плив зі швидкістю 12 км/год, а другий – 15 км/год. Через скільки годин катери зустрінуться?
А) 3 год; Б) 4 год; В) 5 год; Г) 6 год.
7. На склад завезли а ящиків з цукерками, у кожному з яких по 12 кг, та b ящиків з печивом, в кожному з яких по 10 кг. Відомо, що a > b. На скільки більше кілограмів цукерок завезли на склад, ніж печива. Запишіть розв’язок у вигляді буквеного виразу.
A) (12а) : (10b); Б) (12 + а) – (10 + b);
B) 12а – 10b; Г) 12а + 10b.
8. Розв’яжіть рівняння (х – 2735) + 5137 = 9307.
А) 6905; Б) 1435; В) 17179; Г) 11709.
9. Майстер виготовляє 51 деталь за 3 години, а учень 48 деталей за 4 години. За скільки годин вони вдвох виготовлять 145 деталей?
А) 7 год; Б) 4 год; В) 6 год; Г) 5 год.
10. Яке число треба підставити замість а, щоб коренем рівняння 10х + а = 375 було число 25?
А) 35; Б) 125; В) 75; Г) 40.
11. Продуктивність двох верстатів з програмним управлінням однакова. Один з них працював 7 годин, а інший – 3 години. Перший верстат виробив на 140 деталей більше, ніж другий. Яка продуктивність кожного верстата?
A) 34 деталі за годину; Б) 37 деталей за годину;
B) 14 деталей за годину; Г) 35 деталей за годину.
12. У трьох кошиках разом 53 абрикоси. У другому кошику абрикосів удвічі більше, ніж у першому, а в третьому кошику абрикосів на 5 більше, ніж у першому. Скільки абрикосів у третьому кошику?
А) 17; Б) 24; В) 12; Г) 36.
Завдання для перевірки знань № 3 (§10 – §13)
1. Першого дня магазин продав 20 кг яблук, а другого дня – на а кг більше. Скільки кілограмів яблук продав магазин другого дня?
2. Яке із чисел 3, 7, 9 є коренем рівняння
(12 – х) + 14 = 17?
3. Лазерний принтер надрукував 56 сторінок за
8 хвилин. Скільки сторінок за хвилину друкує принтер?
4. Розв’яжи рівняння:
1) х ∙ 140 = 3920; 2) х : 207 = 253.
5. При якому значенні а буде правильною рівність 5а + 4а = 81?
6. Товарний поїзд, що рухається зі швидкістю 50 км/год, долає деяку відстань за 11 год. За скільки годин він подолає цю відстань, якщо збільшить швидкість на 5 км/год?
7. Розв’яжи рівняння (2975 + х) – 4598 = 7459.
8. Сума двох чисел дорівнює 740. Знайди ці числа, якщо одне з них утричі більше за інше.
9. Учень придбав 6 наклейок по а коп. за наклейку і ще 89 коп. у нього залишилося. Склади буквений вираз для обчислення кількості грошей х, які були в учня, та обчисли значення х, якщо а = 95.
10. Додаткове завдання. Спрости вираз (4979 – t) + 5921 та знайди його значення, якщо t = 3597.
11. Додаткове завдання. О восьмій годині ранку
З пункту А зі швидкістю 75 км/год виїхав пасажирський поїзд. Одночасно з ним з пункту В, який знаходиться на відстані 100 км від пункту А, виїхав у тому самому напрямі товарний поїзд, швидкість якого 50 км/год. О котрій годині з пункту А має виїхати швидкий поїзд, швидкість якого 100 км/год, щоб наздогнати товарний потяг одночасно з пасажирським?