Розв’язування задач і вправ на додавання і віднімання дробів з однаковими знаменниками
Урок № 6
Тема. Розв’язування задач і вправ на додавання і віднімання дробів з однаковими знаменниками
Мета уроку. Відпрацьовувати і вдосконалювати навички розв’язування завдань. Що передбачають виконання дій додавання і віднімання дробів з однаковими знаменниками. Розвивати культуру математичної мови та записів. Виховувати здібності до математики.
Тип уроку: застосування навичок і вмінь.
Обладнання: картки із завданнями, таблиці: “Додавання дробів з однаковими знаменниками”, “Віднімання дробів з однаковими
Хід уроку
І. Організаційний момент
ІІ. Перевірка домашнього завдання
Вияснити, які труднощі виникли в учнів під час виконання домашнього завдання. Зібрати зошити на перевірку.
ІІІ. Актуалізація опорних знань.
На дошці зображені таблиці з якими працюють учні.
1. Знайти суму:
. . .
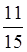
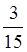
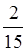
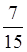
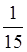
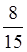
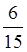
2
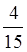
2. Знайти різницю:
. . .
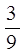
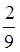
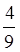
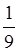
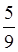
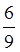
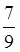
3
ІV. Вдосконалення вмінь
1. Виконати усно. № 1002, № 1004, № 1005.
2. Робота в групах.
Клас поділений на 3 групи. В кожну групу входять учні різних рівнів.
Учні ІV рівня – це консультанти. Групи отримують картки.
Завдання І групи:
Виконати дії:
А)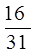 
+
+
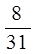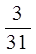; б) 
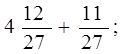
Завдання ІІ групи:
Виконати дії:
А)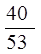 
– 
– 
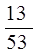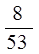; б)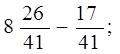 
Завдання ІІІ групи:
Виконати дії:
А)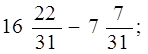 
б)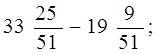 
Закінчивши роботу кожна група обговорює результати з учителем. Потім представник від групи записує розв’язання на дошці і пояснює його.
Фізкультхвилинка
Сів метелик на травичку
І рахує рахівничку:
1, 2, 3 – ти метелику лети.
Крильця вже за головою
Тож дивись перед собою.
Випрямляємо хребет,
Крильця зводимо вперед,
Мов метелики, літаєм,
Крильця зводим, розправляєм.
3. Розв’язування вправ.
А) Учні І і ІІ рівня працюють разом.
1). “Роби як я”.
№ 1019 (а)
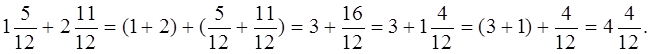
2). Коментоване виконання № 1019 (б)
3). Самостійне виконання з перевіркою № 1019 (в).
Б) Учні ІІІ рівня, консультуючись з учнями-консультантами і вчителем виконують № 1020, № 1022;
В) Учні ІV рівня консультуються з учителем № 1023 (а).
Самостійно виконують № 1023 (в), № 1024, № 1051.
V. Підсумок уроку
1. Як додати дроби з однаковими знаменниками?
2. Як відняти дроби з однаковими знаменниками?
3. Чи користуєтесь ви дробами в повсякденному житті? Приклади.
VІ. Домашнє завдання
§ 22. І і ІІ рівень № 1018, ІІІ рівень № 1021, VІ рівень № 1023 (б), № 1025.
Додатки
Історична довідка
Ви вже знаєте, що натуральні числа виникли в результаті практичної діяльності людей, яким треба було лічити тварин, предмети, вимірювати довжини, площі, об’єми. Але результат вимірювання не завжди можна позначити натуральним числом, бо внаслідок вимірювань найчастіше дістаємо частини прийнятої одиниці.
Так на основі потреб практики виникло поняття дробу – числа, що складається з кількох однакових частин одиниці.
В Єгипті з дробами оперували ще 4000 років тому. Про це свідчать стародавні документи, які збереглися з тих часів. Проте загального способу для позначення всіх дробів, як де прийнято тепер, коли чисельник записують зверху, знаменник знизу, а між ними ставлять риску, в єгиптян не було. При виконанні обчислень стародавні єгиптяни застосовували лише так звані одиничні дроби – дроби з чисельником 1 (і дріб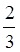 
). Такі дроби єгиптяни зображали, ставлячи крапку над знаменником. Усі інші дроби вони зводили до одиничних. Наприклад, дріб 
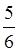подавали у вигляді суми одиничних дробів 
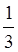і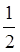 
. Для зведення дробів до одиничних було складено спеціальні таблиці.
Вавілоняни користувалися лише шістдесятковими дробами, тобто дробами, знаменники яких дорівнювали 60 або добутку чисел, кожне з яких дорівнювало 60, наприклад:
60 ∙ 60 = 3600; 60 ∙ 60 ∙ 60 = 216 000 і т. д. Це відповідало прийнятій там шістдесятковій нумерації – застосування шістдесяткових дробів значно спрощувало розв’язання практичних задач.
Вавілоняни багато зробили в галузі астрономії. Тому й не дивно, що шістдесятковими дробами користувалися в астрономічних обчисленнях аж до XVII ст. вчені інших народів і називали ці дроби астрономічними.
На відміну від цих дробів, дроби з будь-яким знаменником назвали звичайними.
У стародавній Греції звичайні дроби були відомі. Понад 2,5 тисячі років тому греки вміли виконувати арифметичні дії з звичайними дробами. Вони користувались і одиничними дробами, і дробами загального виду.
У стародавній Русі дроби називали “частками”, а згодом “ламаними числами”. Окремі дроби мали спеціальні назви.
Наприклад, 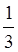– треть, 
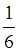– півтреть, 
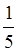– п’ятина, 
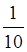– десятина тощо./span>
Запис дробів за допомогою риски став загальноприйнятим з XVI ст.
Колись дії з звичайними дробами завдавали людям надзвичайних труднощів. Ці труднощі у Вавілоні пояснювали “втручанням злих духів”.
Англійський чернець Бєда (VII ст.), який був ученою людиною свого часу, писав: “У світі є багато речей, але немає нічого важчого, як чотири дії арифметики”.
Тоді ж, мабуть, і виникло німецьке прислів’я “попасти в дроби”, що означало опинитися в скрутному становищі. А причина, звичайно, полягала в тому, що не було встановлено правил виконання дій з дробами, не було створено відповідної теорії.
Поряд з цим у VII ст. відомий вірменський учений Ананія Ширакаці (з Ширака) вмів додавати до восьми дробів з різними знаменниками.
Про математику Ананія говорив: І дуже полюбивши мистецтво чисельне, помислив я, що без числа ніяке міркування філософське не складається. Всієї мудрості матір’ю його вважаючи”. Особливий інтерес становлять підручник і задачник з арифметики, який склав Ананія. У ньому наводиться розв’язання задач, що містять додавання дробів, серед знаменників яких є числа: 7, 8, 9, 13, 14, 16, 20.
(1 votes, average: 5.00 out of 5)
Loading...