Розв’язування задач за допомогою рівнянь
Розділ 4 Раціональні числа і дії мідними
§4 9. Розв’язування задач за допомогою рівнянь
Розглянемо приклади розв’язування текстових задач за допомогою рівнянь.
Задача 1. У двох кошиках разом 28 яблук, причому в другому на 4 яблука більше, ніж у першому. Скільки яблук у кожному кошику?
Розв’язання. Позначимо кількість яблук у першому кошику буквою x, тоді кількість яблук у другому буде (x + 4). Загальна кількість яблук x + (x + 4) за умовою задачі дорівнює 28. Маємо рівняння:
X + (x + 4) = 28.
Розв’яжемо це рівняння: x + x + 4 = 28, 2x = 28 –
Отже, в першому кошику було 12 яблук, а в другому – 12 + 4 = 16 (яблук).
Перевірка. У другому кошику яблук на 4 більше, ніж у першому (16 – 12 = 4), в обох кошиках разом 28 яблук (12 + 16 = 28), що відповідає умові задачі.
Відповідь. 12 яблук у першому кошику, 16 яблук – у другому.
Розв’язавши задачу за допомогою рівняння, правильність її розв’язання треба перевірити за умовою задачі, а не за складеним рівнянням.
Отже, розв’язувати задачу за допомогою рівняння можна за таким планом:
1) позначаємо деяку невідому величину (число) буквою, наприклад, х;
2) інші невідомі величини виражаємо
3) виходячи з умови задачі, складаємо рівняння;
4) розв’язуємо це рівняння;
5) знаходимо інші невідомі величини, якщо цього вимагає умова задачі;
6) перевірка (необов’язково);
7) відповідь.
Задача 2. По трьох ящиках розклали 35 банок консервів так, що в першому ящику стало удвічі менше банок, ніж у другому, і на 3 менше, ніж у третьому. По скільки банок консервів стало в кожному ящику?
Розв’язання. Позначимо кількість банок консервів у першому ящику буквою x, тоді кількість банок у другому ящику – 2x, а в третьому – (x + 3). У трьох ящиках разом x + 2x + (x + 3) банок, що за умовою дорівнює 35. Маємо рівняння:
X + 2x + (x + 3) = 35.
Розв’яжемо його: x + 2x + x + 3 = 35, 4x = 35 – 3, 4x = 32, x = 32 : 4, x = 8.
У першому ящику 8 банок, у другому – 2 ∙ 8 = 16 (банок), у третьому – 8 + 3 = 11 (банок).
Перевірку зробіть самостійно.
Відповідь. У першому ящику 8 банок, у другому – 16 банок, у третьому – 11 банок.
Поясни, як за допомогою рівнянь розв’язати задачі 1 і 2. Які етапи можна виділити, розв’язуючи задачу за допомогою рівняння?
1360. (Усно) Перше із чисел на 8 менше за друге. Менше із чисел позначено через x. Вирази через x друге число.
1361. Перше із чисел на 5 більше за друге. Більше із чисел позначено через x. Вирази через х менше число.
1362. (Усно) Перше із чисел у 3 рази менше від другого. Менше із чисел позначено через x. Вирази через x друге число.
1363. Площа двох ділянок дорівнює 48 га. Знайди площу кожної з ділянок, якщо площа першої на 12 га менша за площу другої.
1364. У двох вагонах метро разом 78 пасажирів, причому в першому вагоні пасажирів на 6 менше, ніж у другому. По скільки пасажирів у кожному з вагонів?
1365. Дріт довжиною 508 м розрізали на дві частини, перша з яких у 3 рази довша за другу. Знайди довжину кожної частини.
1366. 42 пакети розклали по двох ящиках так, що в першому пакетів удвічі більше, ніж у другому. По скільки пакетів у кожному з ящиків?
1367. Число х додали до числа, яке дорівнює подвоєному числу х, і одержали 72. Знайди х.
1368. Від числа 56 відняли число x і одержали потроєне число x. Знайди x.
1369. Промінь ділить розгорнутий кут на два кути. Знайди ці кути, якщо один з них на 30° більший за другий.
1370. Промінь ділить прямий кут на два кути. Знайди ці кути, якщо один з них удвічі більший за другий.
1371. Одна із сторін трикутника дорівнює 10 см, а друга сторона – удвічі більша за третю. Знайди довжини двох невідомих сторін трикутника, якщо його периметр 28 см.
1372. Ширина прямокутної ділянки на 10 м коротша від її довжини, а периметр дорівнює 128 м. Обчисли площу ділянки.
1373. Одна із сторін прямокутника на 8 см менша за другу, а його периметр дорівнює 44 см. Знайди площу прямокутника.
1374. У саду росте в 5 раз більше яблунь, ніж слив. Скільки росте яблунь і скільки слив, якщо слив на 16 менше, ніж яблунь?
1375. Батько утричі важчий за сина. Знайди, скільки важить батько, якщо він на 52 кг важчий за сина.
1376. Перше число в 2,5 раза більше за друге. Якщо від першого числа відняти 10, а до другого додати 5, то отримаємо рівні між собою числа. Знайди початкові числа.
1377. На одному дереві сиділо в 4 рази більше горобців, ніж на іншому. Коли із цього дерева злетіло 12 горобців, то на обох деревах горобців стало порівну. Скільки горобців сиділо спочатку на кожному дереві?
1378. Середнє арифметичне двох чисел дорівнює 2,6. Знайди ці числа, якщо одне з них утричі більше за друге.
1379. Сергій за контрольну роботу отримав на 2 бали більше, ніж Петро. Скільки балів отримав кожен хлопець, якщо середнє арифметичне їх оцінок дорівнює 9?
1380. У двох пачках 60 книжок, причому кількість книжок у першій пачці становить 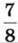 кількості книжок другої. По скільки книжок у кожній пачці?
кількості книжок другої. По скільки книжок у кожній пачці?
1381. Довжина другої стрічки на 3 м більша, ніж довжина першої, причому довжина першої стрічки становить 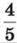 довжини другої. Яка довжина у кожної стрічки?
довжини другої. Яка довжина у кожної стрічки?
1382. У першій бригаді працює на 6 осіб менше, ніж у другій. Скільки осіб працює в кожній бригаді, якщо кількість робітників першої бригади становить 80 % від кількості робітників другої?
1383. У двох хлопців разом 380 наклейок, причому кількість наклейок одного хлопця становить 90 % від кількості наклейок другого. Скільки наклейок має кожен з хлопців?
1384. У першому вагоні в 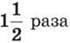 більше вугілля, ніж у другому. Якщо з першого вагона взяти
більше вугілля, ніж у другому. Якщо з першого вагона взяти 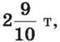 а в другий додати
а в другий додати 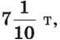 то вугілля у вагонах стане порівну. Скільки тонн вугілля в кожному вагоні?
то вугілля у вагонах стане порівну. Скільки тонн вугілля в кожному вагоні?
1385. На першому самоскиді вантажу в 3 рази менше, ніж на другому. Якщо на перший самоскид додати 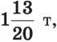 а з другого зняти
а з другого зняти
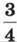 т, то вантажу на обох самоскидах стане порівну. Скільки тонн вантажу на кожному самоскиді?
т, то вантажу на обох самоскидах стане порівну. Скільки тонн вантажу на кожному самоскиді?
1386. У трьох літніх оздоровчих таборах “Орлятко”, “Зірка” та “Дружба” за зміну відпочило 232 школярі. У “Зірці” вдвічі більше дітей, ніж в “Орлятку”, а в “Дружбі” на 16 дітей більше, ніж в “Орлятку”. Скільки школярів відпочило в кожному таборі?
1387. На трьох вантажівках було 5,1 т зерна, причому на другій було зерна удвічі більше, ніж на першій, а на третій – на 0,3 т більше, ніж на першій. Скільки тонн зерна було на кожній вантажівці?
1388. Сума трьох чисел дорівнює 54. Перше число становить 90 % від другого, а третє – 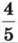 від другого. Знайди добуток цих трьох чисел.
від другого. Знайди добуток цих трьох чисел.
1389. Периметр трикутника дорівнює 46 дм. Довжина другої сторони становить 60 % довжини першої, а довжина третьої сторони – 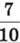 від першої. Знайди довжини сторін трикутника.
від першої. Знайди довжини сторін трикутника.
1390. Велосипедист їхав по шосе зі швидкістю 12 км/год, а по грунтовій дорозі – зі швидкістю 9 км/год. Загалом він подолав 27 км. Скільки часу їхав велосипедист по шосе і скільки по грунтовій дорозі, якщо по грунтовій дорозі він їхав на 0,5 год менше, ніж по шосе?
Розв’язання.

Маємо рівняння 12x + 9(x – 0,5) = 27, розв’язавши яке, отримаємо x = 1,5. Отже, велосипедист їхав 1,5 год по шосе і 1 год по грунтовій дорозі.
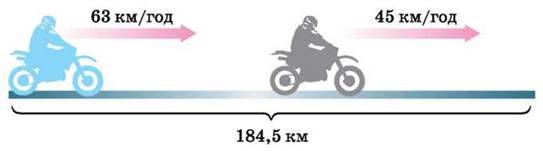
1391. Першу ділянку шляху мотоцикліст долав зі швидкістю 63 км/год, а другу – зі швидкістю 45 км/год. Загалом він подолав 184,5 км. За скільки годин мотоцикліст проїхав першу ділянку шляху і за скільки другу, якщо на першу ділянку він витратив на 0,5 год менше, ніж на другу?
1392. Велосипедист долає відстань між селами за 2 год, а пішохід – за 4,8 год. Знайди швидкість велосипедиста і швидкість пішохода, якщо швидкість пішохода на 7 км/год менша від швидкості велосипедиста.
1393. Кілограм яблук на 4 грн дешевший за кілограм груш, а 5 кг яблук коштують так само, як 3 кг груш. Скільки коштує 1 кг яблук і скільки – 1 кг груш?
1394. Кілограм печива на 12 грн дешевший за кілограм цукерок. За 5 кг печива заплатили стільки, скільки за 3 кг цукерок. Скільки коштує 1 кг печива і скільки – 1 кг цукерок?
1395. У двох маршрутних таксі їхала однакова кількість пасажирів. Після того як з першого таксі вийшло 4 пасажири, а з другого – 12, пасажирів у першому залишилося удвічі більше, ніж у другому. Скільки пасажирів було в кожному таксі спочатку?
1396. На двох полицях книжок було порівну. Після того як з першої полиці зняли одну книжку, а з другої – 19, книжок на першій полиці залишилося утричі більше, ніж на другій. Скільки книжок було на кожній полиці спочатку?
1397. Придбали 8 ручок по 1 грн 60 коп. і по 1 грн 80 коп., заплативши за всю покупку 13 грн 40 коп. Скільки купили ручок по 1 грн 60 коп.?
1398. Придбали 15 зошитів по 1 грн 20 коп. і по 1 грн 80 коп., заплативши за всю покупку 23 грн 40 коп. По скільки зошитів кожного виду було придбано?
1399. У першому баку 55 л олії, а у другому – 45 л. Після того як з першого бака наповнили 8 бутлів, а з другого – 6 таких самих бутлів, олії в баках стало порівну. Скільки літрів олії вміщує один бутель?
1400. У Сергія 54 грн, а в Марійки 66 грн. Після того як Сергій придбав 2 тістечка, а Марійка – 4 таких самих тістечка, грошей у них стало порівну. Скільки коштує одне тістечко?
1401. Перший оператор набирає рукопис на 1,5 год довше, ніж другий, причому за одну годину перший набирає 8 сторінок, а другий – 10 сторінок. Скільки часу витратить перший оператор на набір цього рукопису?
1402. За одну годину учень виготовляє 10 деталей, а майстер – 15 деталей. Певну кількість деталей майстер може виготовити на 2 год швидше, ніж учень. За який час цю кількість деталей виготовить майстер?
1403. Різниця двох чисел 55. Знайди ці числа, якщо 30 % від більшого з них дорівнює  від меншого.
від меншого.
1404. Перше число на 9 більше за друге.  від першого числа дорівнює 50 % від другого. Знайди ці числа.
від першого числа дорівнює 50 % від другого. Знайди ці числа.
1405. У першому баку 140 л води, а в другому – 108 л. Щохвилини з першого бака виливається 5 л води, а з другого – 6 л. Через скільки хвилин у першому баку води залишиться у 2,5 раза більше, ніж у другому?
1406. У першій діжці було втричі більше меду, ніж у другій. Коли з першої діжки взяли 80 кг, а з другої – 30 кг, то в другій діжці меду залишилося на 90 кг менше, ніж у першій. Скільки кілограмів меду було в кожній діжці спочатку?
1407. У першій пачці удвічі більше зошитів, ніж у другій. Після того як з другої пачки 20 зошитів переклали в першу, у другій зошитів стало в 4 рази менше, ніж у першій. Скільки зошитів було в кожній пачці спочатку?
1408. У першому мішку було вдвічі більше борошна, ніж у другому. Після того як з другого мішка пересипали 5 кг у перший, у другому борошна стало втричі менше, ніж у першому. Скільки кілограмів борошна було в кожному мішку спочатку?
1409. Знайди відношення чисел:
1) 15 до 12; 2) 20 до 55; 3) 5,5 до 4,4; 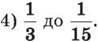
1410. Використовуючи рівність 6 ∙ 3 = 9 ∙ 2, запиши всі можливі пропорції.
1411. Виконай дії:
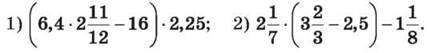
1412. Свіжі сливи містять 60 % води, а чорнослив (сушені сливи) – 15 % води. Скільки свіжих слив треба взяти, щоб отримати 8 кг чорносливу?
1413. З паперової шахової дошки вирізано дві протилежні кутові клітинки (мал. 88). Чи можна після цього розрізати дошку на прямокутники, що містять по 2 клітинки?

Мал. 88
Завдання для перевірки знань № 9 (§ 47 – § 49)
1. Виконай ділення: 1) -12 : (-2); 2) 27 : (-3).
2. Який знак (“+” чи “-“) має корінь рівняння:
1) 2x = -17; 2) -5x = -17?
3. Чи є число -2 коренем рівняння:
1) x + 3 = -1; 2) 4x = -8?
4. Розв’яжи рівняння 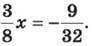
5. Знайди корінь рівняння 3х – 5 = 5х + 9.
6. У баскетбольній секції у 4 рази більше учнів, ніж у секції шахів. Скільки учнів у секції шахів, якщо їх там на 18 менше, ніж у баскетбольній секції?
7. Розв’яжи рівняння 0,3(х – 6) = 0,4(8 – х) – 7,1.
8. У першому кошику яблук було вдвічі більше, ніж у другому. Після того як з другого кошика переклали в перший 3 яблука, у першому кошику яблук стало втричі більше, ніж у другому. Скільки яблук було в кожному кошику спочатку?
Додаткові вправи
9. Знайди значення виразу 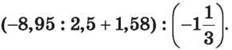
10. Розв’яжи рівняння |5x| + 9 = 12.
11. При яких цілих значеннях а коренем рівняння ax = 8 є ціле число?