Рух точки по колу – КІНЕМАТИКА
ФІЗИКА
Частина 1 МЕХАНІКА
Розділ 1 КІНЕМАТИКА
1.4. Рух точки по колу
Рух матеріальної точки по колу є окремим випадком криволінійного руху. Розглядаючи такі величини, як швидкість  , прискорення
, прискорення 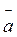 , радіус-вектор
, радіус-вектор 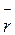 , питання про вибір їхнього напряму не виникало, оскільки воно випливало з їхньої природи. Подібні вектори називають полярними. Вектори типу dφ, напрям яких пов’язаний із напрямом обертання, називають аксіальними. У цьому разі кут можна розглядати
, питання про вибір їхнього напряму не виникало, оскільки воно випливало з їхньої природи. Подібні вектори називають полярними. Вектори типу dφ, напрям яких пов’язаний із напрямом обертання, називають аксіальними. У цьому разі кут можна розглядати
Величину

Де Δt – час, за який здійснюється поворот на кут Δφ, називають кутовою швидкістю точки. Вектор 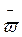 напрямлений уздовж осі, навколо якої обертається тіло. Напрям обертання визначається за правилом правого гвинта. Кутова швидкість – це аксіальний вектор. Модуль вектора кутової швидкості дорівнює
напрямлений уздовж осі, навколо якої обертається тіло. Напрям обертання визначається за правилом правого гвинта. Кутова швидкість – це аксіальний вектор. Модуль вектора кутової швидкості дорівнює 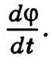 Обертання зі сталою кутовою швидкістю називають рівномірним,
Обертання зі сталою кутовою швидкістю називають рівномірним,
Рівномірний рух можна характеризувати періодом Т. Це час, протягом якого тіло робить один оберт, тобто повертається на кут 2π. Оскільки проміжку часу Δt = Т відповідає кут 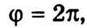 то
то

Частота періодичного процесу

Тоді

Вектор 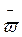 може змінюватись як унаслідок зміни швидкості обертання тіла навколо осі (у цьому разі він змінюється за довжиною), так і за рахунок повороту осі обертання в просторі (у цьому разі
може змінюватись як унаслідок зміни швидкості обертання тіла навколо осі (у цьому разі він змінюється за довжиною), так і за рахунок повороту осі обертання в просторі (у цьому разі 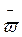 змінюється за напрямом). Нехай за час Δt вектор й дістав приріст Δ
змінюється за напрямом). Нехай за час Δt вектор й дістав приріст Δ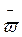 . Зміну вектора кутової швидкості з часом характеризують кутовим прискоренням
. Зміну вектора кутової швидкості з часом характеризують кутовим прискоренням

Вектор 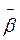 , як і
, як і 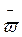 , є аксіальним. Якщо напрям осі обертання в просторі залишається сталим, то кутова швидкість змінюється лише за числовим значенням і |Δ
, є аксіальним. Якщо напрям осі обертання в просторі залишається сталим, то кутова швидкість змінюється лише за числовим значенням і |Δ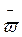 | = Δω. У цьому разі з формули (1.17) дістанемо
| = Δω. У цьому разі з формули (1.17) дістанемо

Вираз (1.18) запишемо у векторній формі

Де β – алгебраїчна величина, яка додатна, якщо ω з часом збільшується (у цьому разі вектори (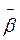 та
та 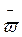 мають однаковий напрям), і від’ємна, якщо й зменшується (у цьому разі напрями
мають однаковий напрям), і від’ємна, якщо й зменшується (у цьому разі напрями 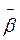 та
та 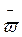 протилежні).
протилежні).
Лінійна швидкість υ визначається кутовою швидкістю обертання тіла ω та відстанню r матеріальної точки від осі обертання. Нехай за малий проміжок часу Δt тіло повертається на кут Δφ. Точка, яка розміщується на відстані r від осі, проходить при цьому шлях

Лінійна швидкість точки
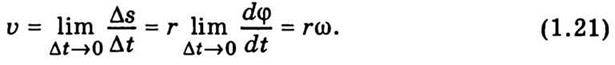
У векторній формі  = . Отже, чим далі розміщується точка від осі обертання, тим з більшою лінійною швидкістю вона рухається.
= . Отже, чим далі розміщується точка від осі обертання, тим з більшою лінійною швидкістю вона рухається.
Знайдемо зв’язок модулів лінійного та кутового прискорення, покладаючи, що r = const. Тоді, виходячи з (1.18), запишемо
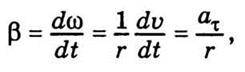
Отже,

При рівномірному русі точки по колу модуль швидкості залишається сталим, але напрям її безперервно змінюється. Розглянемо два вектори швидкості тіла через невеликий проміжок часу Δt. Віднімаючи перше значення швидкості  1 від наступного
1 від наступного  2, дістанемо приріст Δ
2, дістанемо приріст Δ (рис. 1.3). За загальним правилом дії над векторами можна перенести початок векторів швидкості в одну точку (паралельне перенесення). Напрям цих векторів збігається з напрямом дотичної до кола в тій точці, де лежить точка у певний момент. Вектор Δ
(рис. 1.3). За загальним правилом дії над векторами можна перенести початок векторів швидкості в одну точку (паралельне перенесення). Напрям цих векторів збігається з напрямом дотичної до кола в тій точці, де лежить точка у певний момент. Вектор Δ не буде перпендикулярним ні до
не буде перпендикулярним ні до  1, ні до
1, ні до  2. Проте при Δt -> 0 і Δ
2. Проте при Δt -> 0 і Δ -> 0 напрям вектора Δ
-> 0 напрям вектора Δ стає перпендикулярним до вектора швидкості
стає перпендикулярним до вектора швидкості  .
.
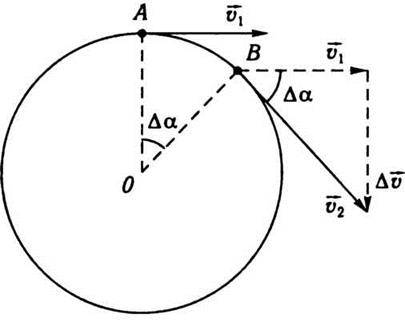
Рис. 1.3.
Отже, нескінченно малий приріст вектора d перпендикулярний до вектора
перпендикулярний до вектора  , тому прискорення
, тому прискорення 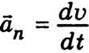 перпендикулярне до швидкості й напрямлене до центра кола. Значення прискорення можна пов’язати зі значенням швидкості
перпендикулярне до швидкості й напрямлене до центра кола. Значення прискорення можна пов’язати зі значенням швидкості  руху тіла по колу й значенням радіуса r. При малому Δφ
руху тіла по колу й значенням радіуса r. При малому Δφ

Де 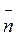 ‘ – одиничний вектор, напрям якого збігається з напрямом вектора Δ
‘ – одиничний вектор, напрям якого збігається з напрямом вектора Δ . Підставляючи в (1.23) Δφ із (1.20), дістанемо
. Підставляючи в (1.23) Δφ із (1.20), дістанемо

Розділивши на Δt праву і ліву частини (1.24) і зробивши відповідні перетворення, дістанемо
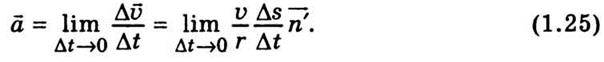
У цьому виразі υ та r – сталі, відношення 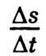 у граничному випадку дає модуль швидкості υ; одиничний вектор
у граничному випадку дає модуль швидкості υ; одиничний вектор 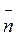 ‘ у граничному випадку збігається з одиничним вектором
‘ у граничному випадку збігається з одиничним вектором 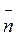 , який перпендикулярний до кола в точці А і напрямлений до центра. Отже,
, який перпендикулярний до кола в точці А і напрямлений до центра. Отже,

Знайдене прискорення напрямлене вздовж нормалі до траєкторії, тобто воно є нормальним.
Якщо матеріальна точка рухається по колу нерівномірно, то крім нормального (його у разі руху по колу називають ще доцентровим) вона матиме тангенціальне прискорення

Яке характеризує зміну швидкості за числовим значенням. Ураховуючи вираз (1.21), для тангенціального прискорення дістанемо

Отже, тангенціальне прискорення зростає лінійно зі збільшенням відстані від осі обертання. Остаточно для вектора прискорення (рис. 1.4) запишемо

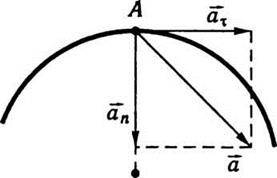
Рис. 1.4