Середня лінія трикутника
Урок № 17
Тема. Середня лінія трикутника
Мета: сформувати в учнів поняття середньої лінії трикутника. Розглянути властивості середньої лінії трикутника та зміст задачі Вариньйона; формувати в учнів уміння: відтворювати вивчені твердження (означення та властивості); виконувати зображення середніх ліній трикутника та здійснювати доведення або спростування того, що даний відрізок є середньою лінією трикутника; відтворювати доведення властивості середньої лінії трикутника та опорної задачі; використовувати властивість середньої
Тип уроку: засвоєння знань, умінь та навичок.
Наочність та обладнання: конспект “Середня лінія трикутника”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Якщо на попередньому уроці учні добре засвоїли навчальний матеріал, то з метою економії часу на уроці перевірці підлягають тільки завдання достатнього та високого рівнів складності (№ 2, 4). Для цього заздалегідь на дошці виконуються рисунки до цих задач, а на уроці озвучується план розв’язання.
III. Формулювання мети і завдань уроку
Учитель повідомляє учням про
IV. Актуалізація опорних знань
З метою підготовки учнів до сприйняття нового поняття та подальшого оволодіння учнями способами дій на застосування нових знань слід активізувати знання і вміння учнів щодо поняття середини відрізка, означення трикутника та його елементів, поняття периметра многокутника, теореми Фалеса, ознак паралелограма.
Виконання усних вправ
1 |
| Знайдіть на відрізки, які є одночасно сторонами не менш як трьох різних трикутників. Назвіть ці трикутники. Чи існують відрізки, які є одночасно сторонами не більш як двох трикутників, зображених на рисунку? |
2 |
| За рисунком складіть задачу і розв’яжіть її |
3 |
| Дано: Довести: АМВН – паралелограм |
4 |
| Дано: ABCD – паралелограм, М – середина ВС, Н – середина AD. Довести: АМСН – паралелограм |
5 |
| Дано: ABCD – паралелограм, AM = СН. Довести: DHBM – паралелограм |
V. Засвоєння нових знань
План вивчення нового матеріалу
1. Означення середньої лінії трикутника.
2. Властивості середньої лінії трикутника.
3. Задача Вариньйона.
@ Вивчення означення середньої лінії трикутника та її властивостей здійснюється традиційно, але слід урахувати такі контрольні моменти:
– після введення означення середньої лінії трикутника слід попрацювати над розумінням учнями змісту сформульованого означення (для цього учням пропонується відповісти на запитання: Скільки середніх ліній можна провести в трикутнику? Чи правильне твердження: “Лінія, що з’єднує середини сторін трикутника, є його середньою лінією”? Або виконати усне завдання за готовим рисунком).
Чи є зображена на рис. 1 лінія середньою лінією трикутника ABC?
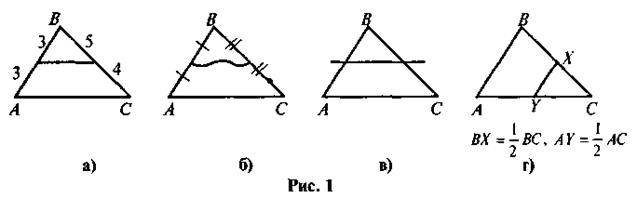
– зміст про властивість середньої лінії трикутника слід опрацювати на розуміння (учні мають усвідомити, що в теоремі мова йде про зв’язок між середньою лінією та стороною, до якої вона є паралельною, тобто середня лінія трикутника не дорівнює половині будь-якої його сторони; а також опанувати спосіб визначення середньої лінії за даною паралельною стороною, та навпаки, знаходження сторони, до якої середня лінія трикутника з даною довжиною паралельна);
– доведення як властивості середньої лінії, так і опорної задачі учні можуть опрацьовувати самостійно (скласти план доведення, за якими вдома будуть його вивчати); після вивчення змісту доведення властивості середньої лінії трикутника слід звернути увагу на те, що безпосередньо з доведення (точніше з використання в ньому теореми Фалеса) випливає справедливість твердження про те, що середня лінія трикутника ділить навпіл будь-який відрізок, один кінець якого лежить на паралельній стороні, а другий кінець виходить з протилежної вершини;
– додатково можна розглянути твердження, що безпосередньо випливають із властивостей середньої лінії трапеції (див. конспект, властивості 3, 4).
Конспект 7 | |
Середня лінія трикутника | |
| Означення. Середньою лінією трикутника називається відрізок, який сполучає середини двох його сторін. |
| |
Властивості | |
1. У будь-якому трикутнику можна провести 3 середніх лінії. 2. Якщо MN – середня лінія? АВС (М – середина АВ, N – середина ВС), то MN || AC, MN = | |
3. Периметр трикутника, утвореного всіма середніми лініями трикутника, дорівнює половині периметра даного трикутника (Р? MNP = | |
4. Три середні лінії трикутника ділять його на чотири рівних трикутники |
VI. Формування первинних умінь
Виконання усних вправ
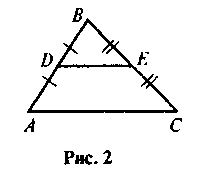
1. Відрізок DE – середня лінія трикутника ABC (рис. 2).
А) Визначте вид чотирикутника ADEC.
Б) Назвіть медіану трикутника, що виходить з вершини А.
2. Чи може середня лінія трикутника бути перпендикулярною до його сторони; до двох його сторін?
3. Чи можуть середні лінії трикутника дорівнювати 3 см, 4 см і 10 см? Чому?
4. У трикутнику ABC проведено середню лінію паралельно стороні АС. У якому відношенні вона ділить медіану ВМ; висоту ВH?
5. Дві середні лінії трикутника рівні між собою і взаємно перпендикулярні. Який це трикутник? Відповідь поясніть.
Виконання графічних вправ
Накресліть трикутник ABC. Позначте на стороні АВ точки А1, А2 і А3 так, щоб вони ділили відрізок АВ на чотири рівні частини. Проведіть через ці точки прямі, паралельні стороні АС, і позначте точки їх перетину зі стороною ВС С1,С2 і С3 відповідно.
А) Виміряйте і порівняйте довжини відрізків, на які точки С1,С2 і С3 ділять сторону ВС.
Б) Виділіть червоним кольором середню лінію трикутника ABC.
Виконання письмових вправ
1. Сторони трикутника дорівнюють 12 см, 16 см і 20 см. Знайдіть сторони трикутника, вершинами якого є середини сторін даного трикутника.
2. Середня лінія трикутника відтинає від нього трапецію з бічними сторонами 3 м і 4 с і меншою основою 5 м. Знайдіть периметр трикутника.
3. Доведіть, що середини сторін ромба є вершинами прямокутника.
Під час розв’язування задачі № 3 слід повторити ознаку прямокутника та використати задачу Вариньйона.
Задача Вариньйона. Середини сторін чотирикутника є вершинами паралелограма.
VII. Підсумки уроку
Які помилки допущено в зображенні середньої” лінії трикутника (див. рис. 3)?
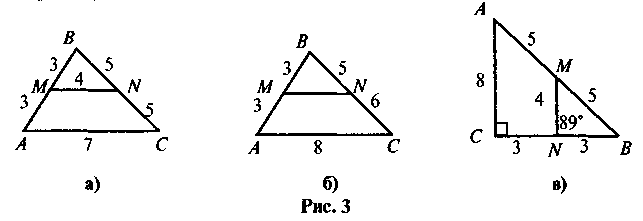
VIII. Домашнє завдання
Вивчити зміст нового теоретичного матеріалу. Розв’язати задачі.
1. Накресліть трикутник ABC. Позначте точки D, Е і F – середини сторін АВ, ВС і АС відповідно. Сполучіть позначені точки.
А) Визначте вид чотирикутника ADEF.
Б) Визначте вид чотирикутника ADEC.
В) Назвіть усі трикутники, що дорівнюють трикутнику DEF. Запишіть відповідні рівності.
2. Середня лінія рівностороннього трикутника дорівнює 3,5 см. Знайдіть периметр трикутника.
3. Діагоналі чотирикутника дорівнюють 18 см і 22 см. Знайдіть периметр паралелограма, вершинами якого є середини сторін даного чотирикутника.
4. Доведіть, що середини сторін прямокутника є вершинами ромба.
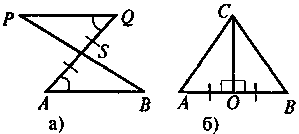
 M +
M + 

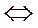

 AC.
AC.