Координати середини відрізка
УРОК № 23
Тема. Координати середини відрізка
Мета уроку: виведення формул для знаходження координат середини відрізка та формування вмінь учнів застосовувати ці формули до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13].
Вимоги до рівня підготовки учнів: записують та доводять формули координат середини відрізка. Застосовують вивчені формули до розв’язування задач.
Хід уроку
І. Перевірка домашнього завдання
Перевірити наявність
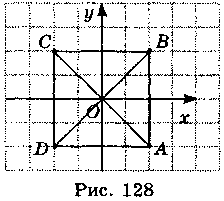
1) В(2; 2), А(2; -2), D(-2; -2) (рис. 128). PABCD = 4 • 4 = 16. SABCD = 42 = 16.
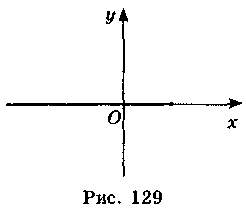
2) а) у = 0, х? 2 (рис. 129);
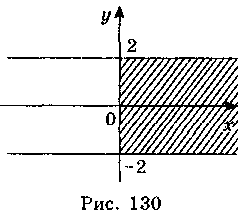
Б) -2 ? y? 2, x? 0 (рис. 130);
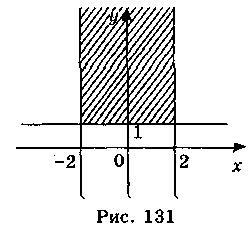
В) |x| ? 2, у? 1 (рис. 131);
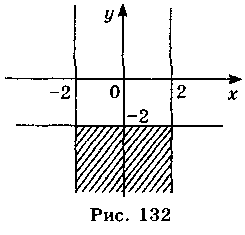
Г) |х| ? 2, у? -2 (рис. 132).
Фронтальна бесіда
1) Як називаються дві перпендикулярні координатні прямі, які перетинаються в початку відліку? 2) Як називають площину, на якій задано систему координат? 3) Як називають координатну пряму, яку
А) вище від осі Ох;
Б) ліворуч від осі Оу;
В) на осі Ох;
Г) на осі Оу.
II. Сприйняття й усвідомлення нового матеріалу
Нехай відрізок АВ має кінці А(х1; у1) і В(х2; у2) і нехай М(х0; у0) – середина відрізка АВ (рис. 133), тоді MD – середня лінія трапеції з основами х1 і х2, МС – середня лінія трапеції з основами у1 і у2. За властивістю середньої лінії трапеції маємо:
, 
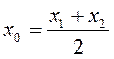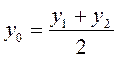. (1)
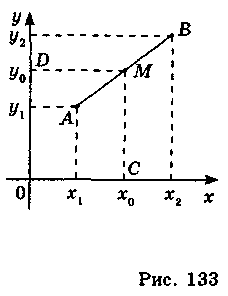
Формули (1) справедливі для будь-якого положення відрізка АВ (рис. 134).
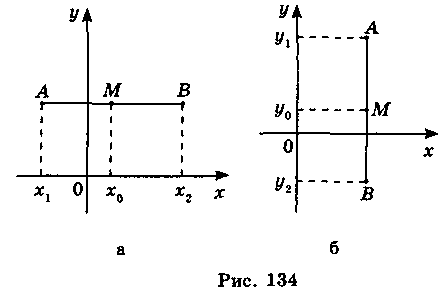
Формули (1) дозволяють за координатами кінців відрізка знаходити координати середини відрізка, а також за координатами середини й одного із кінців відрізка знаходити координати другого кінця.
Виконання вправ
1. Знайдіть координати середини відрізка АВ, якщо:
А) А(5) і В(9);
Б) А(-3) і В(7);
В) А(а) і В(b).
2. Знайдіть координати середини відрізка АВ, якщо:
а) А(3; 2) і В(1; 4); 3. б) А(-3;-2) і В(-1; -2); 4. в) A(a; b) і B(c; d).
III. Закріплення й осмислення нового матеріалу
Виконання завдань
1. Які координати точки С відрізка АВ, якщо АС = ВС і А(0; 2), В(2; 0)? (Відповідь. C(1; 1)) 2. Дано С(2; 6), А(4; 2). Знайдіть координати точки В, якщо відомо, що АС = = ВС і точки А, В, С лежать на одній прямій. (Відповідь. В(0; 10)) 3. Знайдіть координати середин сторін трикутника ABC, якщо А(2; 0), В(2; 2), С(0; 2). (Відповідь. A1(1; 2), В1(1; 1), C1(2; 1).) 4. Коло з центром М(4; 3) проходить через початок координат. Укажіть координати точки N, яка діаметрально протилежить точці О (початку координат). (Відповідь. N (8; 6)) 5. Точки М(-2; 3), N(3; 5), К(3; -5) – середини сторін трикутника ABC. Знайдіть координати вершин цього трикутника. (Відповідь. А(-2; -7), В(-2; 13), С(8; -3)) 6. Якщо А(хА; уА), В(хB; уB), С(хC; уC) – координати вершин трикутника, то М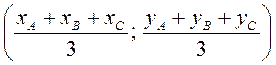
– точка перетину медіан трикутника. Доведіть це. 7. Чотирикутник ABCD задано координатами вершин А(-2; 3), В(0; 6), С(5; 7), D(3; 4). Доведіть, що цей чотирикутник – паралелограм.
Доведення
Доведемо, що діагоналі чотирикутника ABCD точкою перетину діляться навпіл, тобто середини діагоналей збігаються з точкою їх перетину.
Координати середини діагоналі АС: х0 =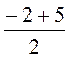 
= 1,5, у0 = 
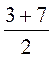= 5, а координати середини діагоналі BD: х’0 = 
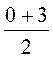= 1,5, y’0 = 
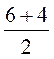= 5.
Діагоналі АС і BD мають спільну середину (1,5; 5), отже, чотирикутник ABCD – паралелограм.
8. Знайдіть координати точки D, якщо ABCD – паралелограм і А(1; 3), В(3; 1), С(3; 3). (Відповідь. D(1; 5))
IV. Домашнє завдання
1. Вивчити формули координат середини відрізка. 2. Виконати завдання. 1) Точка А(-1; 2) лежить на колі з центром (5; -5). Знайдіть координати точки В діаметра АВ. 2) Дано точки А(-1; 3), В(3; 6), К(1; 5). Чи є точка К серединою відрізка АВ? 3) Дано точки А(0; 3), В(3; 8) і С(5; 4). Знайдіть координати кінців середньої лінії трикутника ABC, паралельної АС.
V. Підбиття підсумків уроку
Запитання до класу
Як знайти координати середини відрізка, якщо відомі координати його кінців?
(1 votes, average: 5.00 out of 5)
Loading...