Головна ⇒ 📌Математика ⇒ ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

РОЗДІЛ 8 ВІДСОТКИ. СЕРЕДНЄ АРИФМЕТИЧНЕ

У розділі дізнаєтесь:

Що таке відсоток та як його позначають;

Як подати відсоток десятковим та звичайним дробом;

Як знаходити відсоток від числа;

Як знаходити число за його відсотком;

Як знаходити середнє арифметичне чисел та середнє значення величин;

Як застосувати вивчений матеріал на практиці

ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

§ 34. ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА.

Подивіться на малюнок 226. На ньому ви бачите плитку шоколаду, пачку морозива, на яких написано

“56 % какао”, “пломбір 100 %”. Ви, напевно, чули, як читають такі записи дорослі: “56 відсотків (процентів)”, “100 відсотків”. А що таке відсоток?

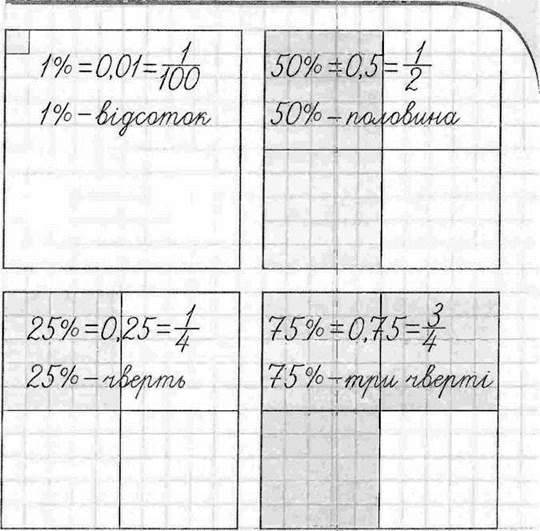
Відсотком (процентом) називається одна сота частина.

ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

Мал. 226

Коротко записують 1 %. Знак % заміняє слово “відсоток”.

ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

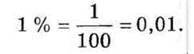
Яке б число або величину ми не взяли, його сота частина – це один відсоток даного числа або величини. Наприклад, 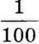ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА числа 400 (0,01 числа 400) – це число 4, тому 4 – це 1 % числа 400; 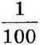ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА гривні (0,01 гривні) – це 1 копійка, тому 1 копійка

– це 1 % гривні.

Задача 1. Пазл містить 500 елементів. Скільки елементів припадає на 1 його відсоток?

Розв’язання, Нехай 500 елементів пазла – це 100 %. Тоді на 1 % припадає у 100 разів менше його елементів. Звідси 500 : 100 = 5 (ел,). Отже, 1 % – це 5 елементів пазла.

Зверніть увагу

Щоб знайти 1 % від числа а, треба це число поділити на 100. Тобто:

100 % – а

1 % – а : 100

Знаючи, яке число або величину становить 1 % , можна знаходити число або величину, які припадають на декілька відсотків.

Задача 2. Маринці треба пришити тасьму, 3 см якої становить 1 % від її довжини. Маринка пришила 50 % тасьми. Скільки сантиметрів тасьми вона прийшла?

Розв’язання. Оскільки 50 % більше за 1 % у 50 разів, значить, Маринка пришила тасьми в 50 разів більше, ніж 3 см. Звідси 3 ∙ 50= 150 (см). Отже, маринка пришила 150 см тасьми.

Зверніть увагу:

Якщо число b становить 1 % від деякого числа, то число, яке припадає на n % , у n разів більше за число b. Тобто:

1 % – b

N % – bn

На практиці часто трапляється так, що обидві наведені задачі треба розв’язувати разом – спочатку знайти, яке число або величина припадає на 1 %, а потім – на декілька відсотків. Такі задачі називають задачами на знаходження відсотка від числа. їх можна розв’язувати як арифметичним, так і алгебраїчним способами.

Задача 3. Груші солодких сортів містять 15 % цукру. Скільки цукру міститься в 3 кг груш?

Розв’язання, Складемо короткий запис даних задачі.

Груші – 3 кг – 100 %

Цукор – ? – 15 %

1. Арифметичний спосіб.

1. Скільки кілограмів відповідає 1 %?

3 : 100 = 0,03 (кг).

2. Скільки кілограмів припадає на 15%?

0,03∙15 = 0,45 (кг).

Отже, у 3 кг груш міститься 0,45 кг цукру.

Можемо сформулювати правило знаходження відсотка від числа.

Правило знаходження відсотка від числа.

Щоб знайти відсоток від числа, треба дане число поділити на 100 і результат помножити на кількість відсотків.

ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

Зверніть увагу:

1) якщо число а становить 100 %, то 1 % – це а :100;

2) якщо шукане число х становить n %, то 1 % – це х : n;

3) значення 1 % можна прирівняли. Тобто: х : n = а: 100

Якщо відсоток подати десятковим дробом, то, щоб знайти відсоток від числа, достатньо дане число помножити на цей десятковий дріб.

Дізнайтеся більше

Слово відсоток (процент) походить від латинського “procentum”, що в перекладі означає “сота частина”, “на сто”. Одну тисячну частину деякої величини називають проміле (від лат. “pro mille” – за тисячу). Проміле позначається символом “%о”. У проміле визначають солоність води, нахил річки, вміст алкоголю в крові, ухил рейкових шляхів у підземних виробках (за правилами безпеки вони мають становити від 3 до 5 %о) тощо.

1 %о = 0.1 % = 0,001.

РОЗВ’ЯЖІТЬ ЗАДАЧІ

1454. Чи правильно, що 1 % дорівнює:

ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

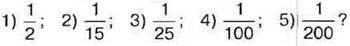
1455. Чи правильно, що 1 % дорівнює:

1)0,1; 2)0,01; 3)0,001; 4)0,11; 5)0,111?

1456. Чи правильно, що 25 % дорівнюють:

ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

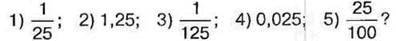
1457. Чи правильно, що 0,75 дорівнює:

1)705%; 2)750%; 3)57%; 4)75%; 5)0,75%?

1458. Чи правильно, що 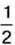ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА дорівнює:

1) 2 %; 2) 20 %; 3) 0,2 %; 4) 12 %; 5) 50 %?

1459 . Подайте десятковий дріб у вигляд її відсотків:

1)0,05; 2)0,13; 3)0,48; 4)0,69; 5)1,23; 6)4,56.

1460. Подайте десятковий дріб у вигляді відсотків:

1)0,02; 2)0,21; 3)0,37; 4)0,81; 5)1,37; 6)7,95.

1461. Запишіть у вигляді десяткового дробу:

1) 6 %; 2) 27 %; 3) 56 %; 4) 92 %; 5) 145 %; 6) 371 %.

1462. Запишіть у вигляді звичайного дробу або мішаного числа:

1) 11%; 2) 34%; 3) 62%; 4) 78%; 5) 139%; 6) 429%.

1463. Якими даними треба доповнити таблицю 45?

Таблиця 45

ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА

1464. У конструкторі 200 елементів. Скільки елементів припадає на 1 %?

1465. Оленка прочитала 25 % книги. Скільки сторінок прочитала Оленка, якщо 1 % становить 3 сторінки книги?

1466. Обчисліть:

1)5% від 60; 3) 60 % від 45; 5) 75 % від 150;

2) 15 % від 30; 4) 25 % від 40; 6) 30 % від 90.

1467. Обчисліть:

1)2% від 40; 3)40% від 32; 5) 65% від 120;

2) 20% від 20; 4) 45% від 90; 6) 35% від 350.

1468. Обчисліть:

1)4% від 6,4; 3)30% від 1,2; 5) 75% від 3,4;

2) 15% від 5,4; 4) 25% від 4,4; 6) 90% від 0,9.

1469. Річка Ворскла має довжину 464 км. На територію Полтавщини припадає 48,7 % усієї її довжини. Скільки кілометрів Ворскли протікає територією Полтавської області?

1470. Ялпуг – найбільше природне озеро в Україні, його довжина – 25 км, а ширина становить 28 % довжини. Яка ширина озера Ялпуг?

1471. У басейні річки Рось, правої притоки Дніпра, знаходиться 1136 малих річок, з них у Київській області – 47 % річок, а в Черкаській – 4 %, інші – у Житомирській та Вінницькій областях. Скільки малих річок з басейну Росі знаходиться на території Київської та Черкаської областей?

1472. Синевир – національний парк в Українських Карпатах. Його загальна площа – 40400 га, з них – 14,4 % відведено під заповідну зону. Яка площа заповідної зони Синевиру?

1473. З молока виходить 6,25 % сиру “Пармезан”. Скільки кілограмів такого сиру можна отримати з молока об’ємом:

1) 300 л; 2) 1000 л; 3)16л?

1474. З молока виходить 21% вершків. Скільки літрів вершків можна отримати з молока об’ємом:

1) 25 л; 2) 160 л; 3)350л?

1475. Із цукрових буряків отримують 16% цукру. Скільки кілограмів цукру можна отримати з цукрових буряків масою:

1) 400 кг; 2) 1500 кг; 3) 12 т?

1475. Сплав золота та срібла містить 36% золота. Скільки золота та срібла міститься у сплаві масою:

1) 150 г; 2) 1 кг; 3) 3,5 кг?

1477. Сплав міді та олова містить 42% міді. Скільки міді та олова міститься у сплаві масою:

1) 140 г; 2) 10 кг; 3) 5,6 кг?

1478. У 5-А класі навчається 34 учні, y 5-Б – 36 учнів. 10 % усіх учнів п’ятих класів – відмінники. Скільки відмінників серед п’ятикласників?

1479. Дитячий хор музичної школи відвідують 60 учнів; з них – 44 дівчинки, а решта – хлопчики. 251% хлопчиків – учасників хору – грають на скрипці. Скільки хлопчиків співають у хорі і грають на скрипці?

1480. Знайдіть суму:

1) 16 % від 16 і 34 % від 16; 2) 25 % від 24 і 65 % від 24.

1481. Знайдіть різницю:

1) 56 % від 12 і 44 % від 12; 2)125 % від 36 і 65 % від 36.

1482. Порівняйте:

1) 10 % від 16 і 16 % від 16; 2) 25 % від 24 і 24 % від 25.

1433. Порівняйте:

1)5% від 200 і 50 % від 20; 2) 25 % від 1,6 і 200 % від 0,25.

1484. Знайдіть суму:

1) 12 % від (1,6 + 8,4) і 34 % від 10;

2) 50 % від (3,6 + 4)і 60 % від (12,4 – 4,6).

1485. Знайдіть різницю:

1) 40 % від (12,5 + 35,5) і 40 % від 38;

2) 120% від (36,4+ 33,6) і 120% від (106-56).

1486. Сума довжин усіх ребер прямокутного паралелепіпеда дорівнює 100 см. Довжини ребер паралелепіпеда становлять 5 %, 8 % та 12 % цієї суми. Обчисліть об’єм паралелепіпеда.

1487. Площа однієї грані прямокутного паралелепіпеда дорівнює 40 см2. Площі двох інших граней становлять відповідно 25 % і 40 % площі першої грані. Знайдіть суму площ усіх граней паралелепіпеда.

1488. У трикутнику одна сторона дорівнює 8 см, друга – становить 125 % від першої, а третя – 60 % від другої. Знайдіть периметр трикутника.

1489. Сума площ двох квадратів дорівнює 80 см2. Площа одного з них становить 20 % цієї суми. Обчисліть периметри обох квадратів.

1490. Сплав олова і свинцю містить олова на 20 % більше, ніж свинцю. Скільки олова і скільки свинцю міститься в 350 г сплаву?

1491. В Олени Петрівни було 3 год для того, щоб приготувати святкову вечерю. 15 % усього часу вона витратила на приготування салату, 45 % часу – на приготування гарячої м’ясної страви, а решту часу – на десерт. Скільки часу витратила Олена Петрівна на приготування кожного блюда?

1492. Маринка прочитала книгу, в якій 300 сторінок, за три дні. Першого дня вона прочитала 30 % усієї книги, другого дня – 40 % від тих сторінок, що залишились, а третього дня – решту. Скільки сторінок дівчинка прочитала, третього дня?

1493. Магазин отримав 50 іграшок на суму 1000 грн. Оптова націнка становить 2 %, а торгова надбавка – 5 %. Знайдіть роздрібну ціну іграшки.

1494. Скільки води потрібно долити до 200 г 10 %-го розчину солі, щоб отримати 4 %-й розчин?

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

1495.Татові Олесі 36 років. Скільки років Олесі, якщо її вік становить 25 % віку тата?

1496. Зріст тата Олесі дорівнює 175 см. Який зріст Олесі, якщо він становить 72 % зросту тата?

1497.Олеся полюбляє грати з татом у нарди. За останній місяць вони зіграли 20 партій, з них 70 % партій виграв тато. Скільки партій виграла Олеся?

ЗАДАНІ НА ПОВТОРЕННЯ

1498. Знайдіть відстань між точками:

1) А (12) і В (39); 2) С (27) і D (41); 3) М (123) і N (98).

1499. Знайдіть різницю найменшого шестицифрового і найбільшого п’ятицифрового чисел.

1500. Основа рівнобедреного трикутника дорівнює 16 см, а бічна сторона менша від неї на 5 см. Знайдіть периметр трикутника.

1501. Сума чотирьох чисел дорівнює 162. Друге число на 12 більше за перше, третє – на 12 більше за друге, а четверте – на 6 більше за третє. Знайдіть їді числа.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Множення трицифрових чисел на двоцифрові. Задачі на знаходження числа за двома різницями. Задачі на знаходження дробу від числа і числа за ного дробом (№№ 928-934) Тема. Множення трицифрових чисел на двоцифрові. Задачі на знаходження числа за двома різницями. Задачі на знаходження дробу від числа і числа за ного дробом (№№ 928-934). Мета. Ознайомити учнів із множенням трицифрових чисел на двоцифрові; закріплювати вміння учнів розв’язувати задачі на знаходження числа за двома різницями; удосконалювати вміння учнів розв’язувати задачі на знаходження дробу від […]...

  2. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА Цілі: – навчальна: удосконалити вміння виконувати вправи, у яких передбачено знаходження дробу від числа; – розвивальна: формувати вміння бачити закономірності, міркувати за аналогією; – виховна: виховувати наполегливість у досягненні мети, творче ставлення до справи; Тип уроку: удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ____________________________________________ ____________________________________________ ____________________________________________ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ […]...

  3. Складені задачі, які містять знаходження дробу від числа Складені задачі, які містять знаходження дробу від числа 1 Знайди: 1) від 98; від 95; від 51; від 64. 2) число, якщо його становлять 98; Число, якщо його становлять 95. 2 Знайди, скільки: Метрів у км, у км; кілограмів у ц, у т. 3 Знайди, записавши відповідні вирази. 1) числа b; числа 125; числа k; […]...

  4. ЩО ТАКЕ ВІДСОТОК Цілі: – навчальна: домогтися засвоєння поняття відсотка, розуміння того факту, що всій величині відповідає 100 %; сформувати вміння записувати відсотки у вигляді десяткового дробу, виконувати вправи, які передбачають використання поняття відсотка; – розвивальна: розвивати пізнавальні здібності учнів; – виховна: виховувати інтерес до вивчення математики; Тип уроку: засвоєння нових знань і вмінь. Обладнання та наочність: Хід […]...

  5. МНОЖЕННЯ Й ДІЛЕННЯ НА РОЗРЯДНІ ОДИНИЦІ 10; 100. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНОЮ І ЧАСТИНИ ВІД ЧИСЛА Мета: вдосконалювати вміння розв’язувати задачі на знаходження числа за його частиною і частини від числа; закріплювати навички ділення і множення на одноцифрове число, на розрядну одиницю 10; 100; розвивати мислення; виховувати уважність. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання Завдання 80 – Прочитайте відповідь, поясніть вибір дії. […]...

  6. Вправи на знаходження частини числа. Письмове ділення на одноцифрове число. Задачі, які включають знаходження частини числа (№№ 62-70) Тема. Вправи на знаходження частини числа. Письмове ділення на одноцифрове число. Задачі, які включають знаходження частини числа (№№ 62 – 70). Мета. Формувати вміння розв’язувати задачі, які включають знаходження частини числа; закріплювати навички ділення трицифрового числа на одноцифрове. Обладнання. Таблиця усних обчислень (гра “Комп’ютер”); картки для опитування; схеми задач. Зміст уроку І. Контроль, корекція і […]...

  7. Знаходження числа за його відсотком Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 43. Знаходження числа за його відсотком Ми вже вміємо знаходити відсоток від числа. Розглянемо задачу знаходження числа за його відсотком. Задача. Учень прочитав 120 сторінок, що становить 30 % числа всіх сторінок у книжці. Скільки сторінок у книжці? Розв’язання. 1-й спосіб. Знайдемо кількість сторінок, яка припадає […]...

  8. Знаходження числа за його частиною. Письмове ділення на одноцифрове число. Задачі на знаходження числа за його частиною (№№ 71-81) Тема. Знаходження числа за його частиною. Письмове ділення на одноцифрове число. Задачі на знаходження числа за його частиною (№№ 71 – 81). Мета. Формувати вміння розв’язувати задачі, які включають знаходження числа за його частиною; закріплювати навички ділення на одноцифрове число. Обладнання. Таблиця усних обчислень; “Картки для поточного контролю знань”; сигнальні картки. Зміст уроку І. Контроль, […]...

  9. Знаходження відсотків від числа Урок № 57. Тема. Знаходження відсотків від числа Мета уроку. Ознайомити учнів з задачами на знаходження відсотків від числа; сформулювати правило знаходження відсотків від числа, вчити учнів використовувати його при розв’язувані задач. Хід уроку І. Перевірка домашнього завдання Два учні на дошці відтворюють розв’язання домашніх вправ №№ 7,9. тестові завдання стор. 312. ІІ. Повторення вивченого […]...

  10. ЗНАХОДЖЕННЯ ЧАСТИНИ ЧИСЛА. ПИСЬМОВЕ ДІЛЕННЯ НА ОДНОЦИФРОВЕ ЧИСЛО. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЗНАЧЕННЯМ ЙОГО ДРОБУ Мета: повторити правило знаходження частини числа; закріпити вміння розв’язувати задачі на знаходження частини числа за значенням його дробу; вчити виконувати письмове ділення; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення. Гра “День – ніч” 3. Математичний диктант – Запиши […]...

  11. Знаходження числа за величиною його дробу ст.104 Знаходження числа за величиною його дробу 1 Розв’яжи задачі, записавши розв’язання кожної по діях і виразом. Що спільне в записах одержаних виразів? Прочитай вирази, поясни, що позначає кожне число. Як знайти число за величиною його дробу? 1) Маса левиці 120 кг, що становить маси лева. Визнач масу лева. 2) Бурий ведмідь важить 320 кг, що […]...

  12. Читання і записування чотирицифрових чисел. Знаходження частини числа і числа за його частиною. Задачі, які включають знаходження частини числа (№№ 185-193) Тема. Читання і записування чотирицифрових чисел. Знаходження частини числа і числа за його частиною. Задачі, які включають знаходження частини числа (№№ 185-193). Мета. Ознайомити учнів з правилом записування будь-якого чотирицифрового числа; закріплювати вміння учнів читати чотирицифрові числа; повторити правило знаходження частини числа і числа за його частиною, розв’язувати задачі двома способами. Обладнання. Нумераційна таблиця; таблиця […]...

  13. Знаходження числа за його відсотками Урок 121 Тема. Знаходження числа за його відсотками Мета: узагальнити й систематизувати знання учнів про види задач, що розв’язуються із застосуванням алгоритму знаходження числа за його відсотками; здійснити діагностику засвоєння знань і сформованих умінь учнів. Тип уроку: узагальнення і систематизація знань. Хід уроку I. Розминка Усні вправи 1. Знайдіть числа, яких не вистачає в ланцюжку […]...

  14. Множення і ділення на 10 і на 100. Задачі, які включають знаходження частини числа або числа за його частиною (№№ 82-91) Тема. Множення і ділення на 10 і на 100. Задачі, які включають знаходження частини числа або числа за його частиною (№№ 82 – 91). Мета. Закріпити навички множення і ділення круглих чисел на 10 і на 100; вправляти учнів у розв’язуванні задач, які включають знаходження частини числа або числа за його частиною. Обладнання. Таблиця усних […]...

  15. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНОЮ. ПИСЬМОВЕ ДІЛЕННЯ НА ОДНОЦИФРОВЕ ЧИСЛО. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНОЮ Мета: повторити і закріпити правило знаходження числа за його частиною; вчити розв’язувати задачі на знаходження числа за його частиною, виконувати ділення на одноцифрове число; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ III. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Усні обчислення Гра “Ланцюжок” 40 збільш на 60; зменш на 2; […]...

  16. ЧИТАННЯ І ЗАПИСУВАННЯ ЧОТИРИЦИФРОВИХ ЧИСЕЛ. ЗНАХОДЖЕННЯ ЧАСТИНИ ЧИСЛА ТА ЧИСЛА ЗА ЗНАЧЕННЯМ ЙОГО ЧАСТИНИ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ФОРМУВАТИ ВМІННЯ ЧИТАТИ Й ЗАПИСУВАТИ ЧОТИРИЦИФРОВІ ЧИСЛА; ПОВТОРИТИ ЗНАХОДЖЕННЯ ЧАСТИНИ ЧИСЛА ТА ЧИСЛА ЗА ЙОГО ЧАСТИНОЮ I. Перевірка домашнього завдання На дошці записано вирази: 60 : 12 60 : 12 + 24 : 12 (60 + 24) : 12 Який з них є розв’язком задачі 184? Взаємоперевірка вправи 183. II. Актуалізація та […]...

  17. Задачі на ділення дробів. Знаходження числа за його дробом Урок № 3 3 Тема. Задачі на ділення дробів. Знаходження числа за його дробом Мета: домогтися засвоєння учнями алгоритму розв’язування задач на знаходження числа за його дробом (відсотками); повторити алгоритми розв’язування інших задач на ділення; виробляти вміння розв’язувати задачі на застосування названих алгоритмів. Тип уроку: засвоєння знань та вмінь. Хід уроку І. Актуалізація опорних знань […]...

  18. Знаходження числа за його дробом Розділ 2 Звичайні дроби §18. Знаходження числа за його дробом Розглянемо задачу, що зводиться до знаходження числа за його дробом. Задача 1. Сергій прочитав 120 сторінок. Це становить книжки. Скільки сторінок у книжці? Розв’язання. Умову задачі зображено на малюнку 4. 1) 120 : 3 = 40 (с.) – припадає на Книжки; 2) 40 ∙ 5 […]...

  19. Складені задачі, які містять знаходження дробу від числа ст. 108 Складені задачі, які містять знаходження дробу від числа 1 Розташуй числа в порядку зростання. ; ; ; ; 1; ; ; ; ; ; ; ; 2 Знайди: 1) від 92; від 168; від 81; від 90; 2) число, якщо його становлять 92; число, якщо його становлять 1 бо; число, якщо його становлять 81; число, […]...

  20. Знаходження дробу від числа ст.99 Знаходження дробу від числа 1 Знайди дріб від числа. від 72; від 88; від 48. 2 Зістав задачі 1 і 2. Що в них спільне? відмінне? Розв’яжи задачу 1. Розв’яжи задачу 2. Запиши розв’язання задачі 2 по діях і виразом. Прочитай одержаний вираз і поясни, що позначає кожне числе Спробуй сформулювати, використавши слова “чи сельник” […]...

  21. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА ТА ЧИСЛА ЗА ЙОГО ДРОБОМ РОЗДІЛ 5 ЗВИЧАЙНІ ДРОБИ § 25. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА ТА ЧИСЛА ЗА ЙОГО ДРОБОМ У попередніх параграфах ви дізналися, що таке дріб, з’ясували, що показує чисельник дробу, а що – його знаменник. На практиці доводиться знаходити число, яке від даного числа становить, наприклад, тощо. Такі задачі називають задачами на знаходження дробу від числа. їх […]...

  22. Аналіз контрольної роботи. Частини. Порівняння частин. Задачі на знаходження частини числа і числа за його частиною. Складені задачі, які включають знаходження частин (№№ 751-759) Тема. Аналіз контрольної роботи. Частини. Порівняння частин. Задачі на знаходження частини числа і числа за його частиною. Складені задачі, які включають знаходження частин (№№ 751-759). Мета. Проаналізувати помилки, допущені учнями під час виконання контрольної роботи; вчити учнів знаходити частину числа та число за його частиною; удосконалювати вміння учнів розв’язувати складені задачі, які включають знаходження частин. […]...

  23. Відсотки. Знаходження відсотків від числа Урок 117 Тема. Відсотки. Знаходження відсотків від числа Мета: сформувати вміння, відпрацювати навички знаходження відсотків від числа; провести діагностику засвоєння знань і вмінь. Тип уроку: застосування знань, навичок і вмінь. Хід уроку I. Розминка Усні вправи 1. Розчин містить сіль і воду. Сіль становить 9% розчину. Скільки відсотків становить вода? 2. Сплав складається з міді, […]...

  24. Знаходження дробу від числа Розділ 2 Звичайні дроби §15. Знаходження дробу від числа Розглянемо задачу, що зводиться до знаходження дробу від числа. Задача 1. У класі 30 учнів, із них хлопці. Скільки хлопців у класі? Розв’язання. (Мал. 3). 1) 30 : 5 = 6 (уч.) – становить від 30 учнів; 2) 6 ∙ 2 = 12 (уч.) – становить […]...

  25. Складені задачі, які містять знаходження числа за величиною його дробу Складені задачі, які містять знаходження числа за величиною його дробу 1 Яку частину дециметра складають 7 см? Яку частину доби складають 42 хв? Яку частину тижня складають 3 доби? Яку частину центнера складають 3 кг? 2 Знайди: 1) від 168; від 136; від 144; від 100. 2) число, якщо його становлять 168; число, якщо його […]...

  26. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ Цілі: – навчальна: удосконалити вміння виконувати вправи, у яких передбачено знаходження числа за його дробом; узагальнити та систематизувати знання учнів з теми “Звичайні дроби”; – розвивальна: формувати вміння аналізувати інформацію, узагальнювати та робити висновки; – виховна: виховувати відповідальність за результати своєї роботи, свідоме ставлення до навчання; Тип уроку: комбінований. Обладнання та наочність: Хід уроку І. […]...

  27. ДІЛЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ § 10. ДІЛЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ Ви знаете, що невідомий множник знаходять діленням добутку на відомий множник. Наприклад, у прямокутника з площею дм2 й однією зі сторін дм (мал. 9) друга сторона дорівнює частці від ділення дробу Мал. 9 Нехай шуканою часткою є дріб […]...

  28. Множення іменованих чисел на двоцифрові числа. Порівняння задач на знаходження числа за двома різницями. Запис периметра і площі квадрата у загальному вигляді. Розв’язування задач на знаходження числа за його дробом (№№ 942-949) Тема. Множення іменованих чисел на двоцифрові числа. Порівняння задач на знаходження числа за двома різницями. Запис периметра і площі квадрата у загальному вигляді. Розв’язування задач на знаходження числа за його дробом (№№ 942-949). Мета. Ознайомити учнів із множенням складених іменованих чисел на двоцифрові числа; удосконалювати вміння розв’язувати задачі на знаходження числа за двома різницями, порівнювати […]...

  29. Протилежні числа. Цілі числа. Раціональні числа Розділ 4 Раціональні числа і дії мідними §35. Протилежні числа. Цілі числа. Раціональні числа Точки A і B з відповідними координатами 2 і -2 однаково віддалені від початку відліку – точки О і знаходять ся по різні боки від неї (мал. 71). Щоб потрапити з точки О в точки A(2) і B(-2), треба відкласти однакові […]...

  30. Відсотки. Знаходження відсотків від числа Розділ II ДРОБОВІ ЧИСЛА І ДІЇ З НИМИ § 5. ДЕСЯТКОВІ ДРОБИ 37. Відсотки. Знаходження відсотків від числа На практиці люди часто користуються сотими частинами величин. Наприклад, сота частина гектара – 1 ар (1 сотка), сота частина століття – 1 рік, сота частина гривні – 1 копійка, сота частина метра – 1 сантиметр. Для сотої […]...

  31. Знаходження числа за його частиною. Перевірка письмового ділення множенням УРОК 7 Тема. Знаходження числа за його частиною. Перевірка письмового ділення множенням Мета: розвивати вміння учнів виконувати письмове ділення та розв’язувати задачі, пов’язані з поняттям частина числа; розвивати логічне мислення, увагу. Обладнання: картки з тестами, картки для усної лічби, креслення. ХІД УРОКУ I. Контроль і закріплення знань учнів Тест для перевірки знань, отриманих раніше (Кожне […]...

  32. Відсотки. Знаходження відсотків від даного числа Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 42. Відсотки. Знаходження відсотків від даного числа Під час різних обчислень людям часто доводиться знаходити частини числа: (половину), (четвертину), і т. д. Найзручніше в таких обчисленнях знаходити соті частини числа, або відсотки (проценти)1, оскільки при цьому доводиться множити чи ділити на число 100. Відсотком (процентом) називається […]...

  33. Знаходження числа за значенням його дробу. Розв’язування задач (№№ 788-796) Тема. Знаходження числа за значенням його дробу. Розв’язування задач (№№ 788-796). Мета. Вчити учнів знаходити число за значенням його дробу; вправляти у розв’язуванні задач з дробовими числами; закріплювати вміння знаходити дріб від числа. Обладнання. Таблиця для усних обчислень; картки для опитування; короткий запис задачі. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка домашнього […]...

  34. МНОЖЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ § 9. МНОЖЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ДРОБУ ВІД ЧИСЛА Дроби, як і натуральні числа, можна множити. Наприклад, щоб знайти площу прямокутника зі сторонами 3 см і 4 см, треба помножити ці числа: 3 ∙ 4 = 12 (см2). Але Тому, у квадратних дециметрах площа даного прямокутника дорівнює добутку […]...

  35. Запис дробів. Знаходження дробу від числа. Розв’язування задач (№№ 770-776) Тема. Запис дробів. Знаходження дробу від числа. Розв’язування задач (№№ 770-776). Мета. Ознайомити учнів із знаходженням дробу від числа у випадку, коли чисельник відмінний від одиниці; вчити розв’язувати задачі на знаходження дробу від числа; закріплювати вміння учнів записувати та читати дроби. Обладнання. Таблиця “Знаходження дробу від числа”; картки для опитування; схеми задач. Зміст уроку І. […]...

  36. ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА ЗАДАЧІ НА ПОВТОРЕННЯ ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА 1. Скільки чисел натурального ряду розміщено між числами: 1)120 і 129; 2) 999 і 1100; 3)8901 і 8910; 4) 50000 і 50020? 2. На прямій дано три точки А, В і С. Знайдіть довжину відрізка ВС, якщо АВ = 8 см і АС – 9 см. Скільки розв’язків […]...

  37. ЧИТАННЯ І ЗАПИС ЧОТИРИЦИФРОВИХ ЧИСЕЛ. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНАМИ І ЧАСТИНИ ВІД ЧИСЛА Мета: ознайомити учнів з правилом запису будь-якого чотирицифрового числа; закріплювати вміння читати чотирицифрові числа; повторити правило знаходження частини числа і числа за його частиною; вдосконалювати навички усних і письмових обчислень, розв’язування задач двома способами; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ Завдання 183 – Прочитайте числа, в […]...

  38. Знаходження значень виразів на сумісні дії. Задачі на знаходження числа за двома різницями (№№ 950-958) Тема. Знаходження значень виразів на сумісні дії. Задачі на знаходження числа за двома різницями (№№ 950 – 958). Мета. Закріплювати вміння учнів знаходити значення виразів на сумісні дії; удосконалювати вміння розв’язувати задачі на знаходження числа за двома різницями. Обладнання. Таблиця “Знаходження значень виразів на сумісні дії”; сигнальні картки; таблиця для короткого запису задачі. Зміст уроку […]...

  39. ДІЛЬНИКИ і КРАТНІ НАТУРАЛЬНОГО ЧИСЛА. ПРОСТІ ЧИСЛА Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ У розділі дізнаєтесь: – що таке дільники і кратні натурального числа; – які є ознаки подільності чисел; – які числа називаються простими та як їх знаходити; – як розкласти число на множники; – що таке найбільший спільний дільник чисел та як його знаходити; – що таке найменше спільне кратне чисел […]...

  40. Визначення числа десятків і числа десятків тисяч, числа сотень сотень тисяч, числа одиниць і одиниць тисяч у заданих числах. Розв’язання задач на знаходження 4-го пропорційного способом відношень УРОК 28 Тема. Визначення числа десятків і числа десятків тисяч, числа сотень І Сотень тисяч, числа одиниць і одиниць тисяч у заданих числах. Розв’язання задач на знаходження 4-го пропорційного способом відношень Мета: вправляти учнів у визначенні загальної кількості одиниць певного розряду у заданому числі; розвинути й закріпити вміння учнів розв’язувати задачі на відношення. Обладнання: предметні […]...

Ви зараз читаєте: ЩО ТАКЕ ВІДСОТОК. ЗНАХОДЖЕННЯ ВІДСОТКА ВІД ЧИСЛА
«
»