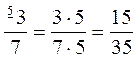Спільний знаменник кількох дробів. Зведення звичайних дробів до найменшого спільного знаменника
Урок № 14
Тема. Спільний знаменник кількох дробів. Зведення звичайних дробів до найменшого спільного знаменника
Мета: на основі основної властивості дробу сформувати уявлення учнів про зміст поняття зведення дробів до спільного знаменника, а також розпочати роботу з вироблення вмінь зводити дроби до найменшого спільного знаменника.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Перевірка домашнього завдання
Оскільки попередня тема опрацьована, то фронтальної перевірки домашнього завдання (задля економії часу) на уроці
ІІ. Актуалізація опорних знань
Усні вправи
1. Обчисліть: |
|
|
2. Знайдіть серед чисел рівні й поясніть:  ;
; 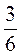 ; 1;
; 1; 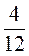 ;
; 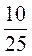 ;
; 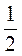 ;
; 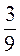 ;
; 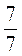 ; 0,5;
; 0,5; 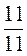 ; 0,4.
; 0,4.
3. Знайдіть НСК чисел (найраціональнішим способом): а) 4 і 8; б) 12 і 16; в) 12 і 11; г) 5; 10; 11.
4. Чи існує таке натуральне
ІІІ. Формування знань
@ На уроці треба розглянути два питання.
1. Що означає “звести дріб до нового знаменника”?
2. Як звести два (і більше дробів) до найменшого спільного знаменника?
Тому й викладення матеріалу можна проводити традиційно, спочатку розглянувши приклад на зведення дробу до нового знаменника, а потім алгоритм зведення дробів до найменшого спільного знаменника.
Результатом такої роботи може бути конспект № 9.
Конспект 9 | |
Зведення дробів до НСЗ | |
1. Зведення одного дробу до нового знаменника:
1) с : b = n – додатковий множник; 2) 2. Зведення кількох дробів до НСЗ (найменший спільний знаменник): 1) знайти НСК знаменників > НСЗ; 2) поділити НСЗ на кожний знаменник > додатковий множник; 3) чисельник і знаменник дробу помножити на додатковий множник | Приклад
Оскільки 96 : 4 = 24, то Приклад Звести Оскільки НСК (5; 7) = 35, то НСЗ = 35. 35 : 5 = 7; 35 : 7 = 5,тому
|
IV. Формування вмінь
@ Відповідно до схеми пояснення матеріалу, розв’язуємо спочатку вправи на:
А) формування вмінь зводити дріб до нового знаменника;
Б) формування вмінь використовувати алгоритм зведення кількох дробів до НСЗ.
Розв’язування вправ
І рівень
Усні вправи
Назвіть дріб зі знаменником 16, який дорівнює дробу: 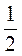 ;
; 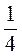 ;
; 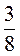 . (Для кращого сприйняття можна умову записати у вигляді рівності:
. (Для кращого сприйняття можна умову записати у вигляді рівності: 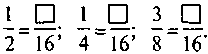 )
)
Знайдіть НСК знаменників дробів: a) 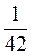 і
і 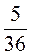 ; б)
; б) 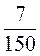 і
і 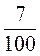 ; в)
; в) 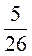 і
і 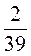 .
.
Краще спочатку просто знайти НСЗ для даних дробів.
ІІ, III рівні
Письмові вправи
1. Зведіть до знаменника 48 дроби: 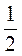 ;
;  ;
; 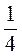 ;
; 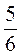 ;
; 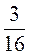 ;
; 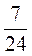 .
.
2. Зведіть до найменшого спільного знаменника дроби: а) 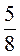 і
і 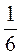 ; б)
; б) 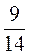 і
і 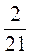 ; в)
; в) 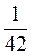 і
і 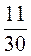 ; г)
; г) 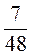 і
і 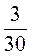 .
.
3. Зведіть до найменшого спільного знаменника дроби: а) 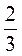 ,
, 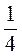 і
і 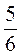 ; б)
; б) 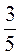 ,
, 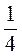 і
і 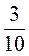 ; в)
; в) 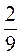 ,
, 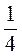 і
і 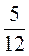 .
.
Додатково доцільно розв’язати задачі на повторення алгоритмів порівняння звичайних дробів з однаковими знаменниками; їх додавання і віднімання, а також матеріалу, пов’язаного із мішаними числами.
Задача1. При яких значеннях а нерівність правильна?
А) 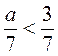 ; б)
; б) 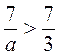 ; в)
; в) 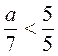 ; г)
; г) 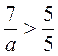 .
.
Задача 2. Домогосподарка приготувала 13 кг вишневого варення і 15 кг полуничного. Вишневе вона розлила порівну в 15 банок, а полуничне – у 17 банок. Скільки кілограмів варення кожного виду було в одній банці?
Задача 3. Знайдіть пропущені букви
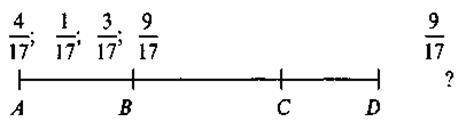
Задача 4. Знайдіть пропущені рисунки:
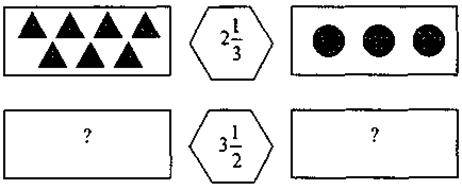
V. Підсумки уроку
Повторити засвоєні терміни і поняття можна під час виконання так званого “німого диктанту”:
@Вчитель заздалегідь за дошкою готує записи, що містять перетворення, розглянуті на уроці, і просто показує об’єкти, назву якого учні повинні були засвоїти. Наприклад:
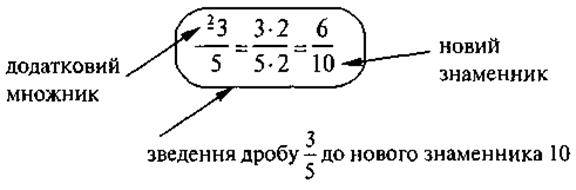
VI. Домашнє завдання
1. Зведіть до знаменника 36 дроби: 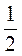 ;
; 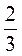 ;
; 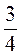 ;
; 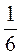 ;
; 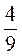 ;
; 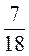 .
.
2. Зведіть до найменшого спільного знаменника дроби: а) 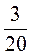 і
і 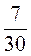 ; б)
; б) 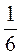 і
і 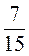 ; в)
; в) 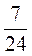 і
і 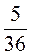 ; г)
; г) 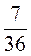 і
і 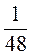 .
.
3. Зведіть до найменшого спільного знаменника дроби: а) 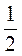 ,
, 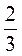 і
і 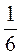 ; б)
; б) 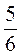 ,
, 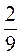 і
і 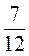 ; в)
; в) 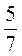 ,
, 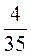 і
і 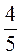 .
.
4. Запишіть неправильним дробом: 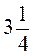 ,
, 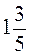 ,
, 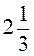 .
.
5. Виконайте дії: а) 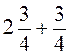 ; б)
; б) 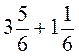 ; в)
; в) 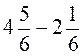 ; г)
; г) 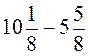 .
.
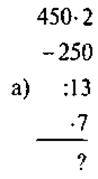
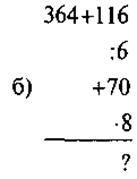
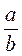 треба звести до знаменника с.
треба звести до знаменника с.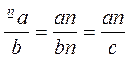 .
.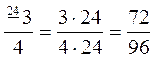 .
.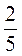 і
і 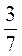 до НСЗ.
до НСЗ.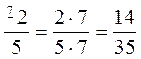 ;
;