Головна ⇒ 📌Формули й таблиці ⇒ Співвідношення між тригонометричними функціями одного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ
Співвідношення між тригонометричними функціями одного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ
Формули й таблиці
МАТЕМАТИКА
ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ
Співвідношення між тригонометричними функціями одного аргументу
Для будь-якого 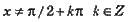
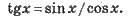
Для будь-якого 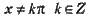
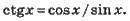
Для будь-якого 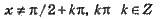
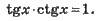
Для будь-якого 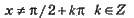
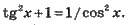
Для будь-якого 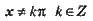
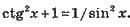
Related posts:
- Співвідношення між прямими й оберненими тригонометричними функціями – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Співвідношення між прямими й оберненими тригонометричними функціями...
- Формули подвійного і потрійного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули подвійного і потрійного аргументу Для будь-якого α Якщо Якщо...
- Основні співвідношення між тригонометричними функціями одного й того самого кута 10. Додатки 34. Основні співвідношення між тригонометричними функціями одного й того самого кута...
- Формули половинного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули половинного аргументу Для будь-якого α Якщо α ≠ (2к +1)π, то Якщо α ≠ 2kπ, то Для тангенса й котангенса половинного аргументу є ще й інші формули, що не містять радикалів. Якщо α ≠ (2к +1)π, то Якщо α ≠ 2kπ, то...
- Співвідношення між тригонометричними функціями одного аргументу УРОК 12 Тема. Співвідношення між тригонометричними функціями одного аргументу Мета уроку: вивчення співвідношення між тригонометричними функціями одного аргументу, формування умінь застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, знаходження значень тригонометричних функцій за однією відомою функцією. І. Аналіз контрольної роботи II. Мотивація навчання Дуже часто при розв’язуванні задач виникає проблема: знайти значення тригонометричних функцій, якщо […]...
- Формули перетворення добутків у суми – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення добутків у суми Для будь-яких α і β...
- Формули перетворення сум у добутки – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення сум у добутки Для будь-яких α і β...
- Основна тригонометрична тотожність – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основна тригонометрична тотожність Для будь-якого x...
- Формули зниження степеня – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули зниження степеня Для будь-якого α Якщо , то Якщо α ≠ kπ, то...
- Основні тригонометричні тотожності – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні тотожності...
- Формули додавання – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули додавання Для будь-яких α, β Для будь-яких α й β, якщо то А якщо то...
- Основні тригонометричні рівняння – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні рівняння Sin x = 0 X = πk, k Z Cos x = 0 X = π/2 + 2πk, k Z Sin x = 1 X = π/2 + 2πk, k Z Cos x = 1 X = 2πk, k Z Sin x = -1 X […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- Тригонометричні функції числового аргументу Математика – Алгебра Тригонометричні функції Тригонометричні функції числового аргументу Розглянемо одиничне (тригонометричне) коло, центр якого розташований у точці і радіус якого дорівнює 1 (див. рисунок). Нехай точка P0 – це точка (1; 0). Кожну іншу точку кола можна дістати поворотом P0 навколо початку координат. Будемо вважати від’ємним напрямок повороту за годинниковою стрілкою, додатним – проти. […]...
- Формули скороченого множення – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Формули скороченого множення (а + b)2 = а2 + 2аb + b2 (квадрат суми); (a – b)2 = а2 – 2ab + b2 (квадрат різниці); A2 – b2 = (a + b)(a – b) (різниця квадратів); (a + b)3 = а3 + 3а2b + 3ab2 + b3 (куб суми); […]...
- Формули приведення – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули приведення π/2 ± α π ± α 3 π/2 ± α 2π ± α 90° ± α 180° ± α 270° ± α 360° ± α Sin β Cosα Sinα -cosα ±sinα Cos β Sinα -cosα ±sinα Cosα Tg β Tgα ctgα Tgα Tgα ctgα ±tgα Ctg β […]...
- Тригонометричний запис комплексного числа – КОМПЛЕКСНІ ЧИСЛА Формули й таблиці МАТЕМАТИКА КОМПЛЕКСНІ ЧИСЛА Тригонометричний запис комплексного числа Z = r (cosα + isinα) R = – модуль комплексного числа; α – аргумент комплексного числа; Значення α, узяте в межах одного кола, -π < α < π називається головним значенням аргументу....
- ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Для будь-якого додатного числа а, що не дорівнює 1: 1) loga1 = 0; 2) logaa = 1; 3) якщо х > 0 і у > 0, то logaху = logaх + logaу; 4) якщо х > 0 і у > 0, то logax/y = logax – logaу; 5) […]...
- Формули Математика – Алгебра Натуральні числа і дії над ними Формули Якщо співвідношення між якимись змінними записане у вигляді рівності, така рівність називається Формулою. Приклади Формула периметра квадрата , де P – периметр квадрата, а – сторона квадрата. Формула відстані , де s – відстань, v – швидкість, t – час. Формула площі прямокутника , де […]...
- Визначення структурної формули – Визначення формули АНАЛІЗ ОРГАНІЧНИХ СПОЛУК 1.4 . Визначення структурної формули Для знайденої молекулярної формули спочатку записують усі можливі ізомерні структури. Далі перевіряють типові властивості цих речовин, щоб встановити, яка структурна формула підходить до визначуваної речовини. Приклад. Для молекулярної формули С2Н60 маємо дві можливі структурні формули. Етанол розчиняється у воді (водневий зв’язок), а етер не розчиняється. Етанол на […]...
- Основні властивості арифметичного квадратного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості арифметичного квадратного кореня Для будь-яких дійсних чисел а й b: 1) якщо а ≥ 0, , то а = ()2; 2) = |a|; 3) якщо а ≥ 0 й b ≥ 0, то = ; 4) якщо а ≥ 0 й b > 0, то ; […]...
- Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Урок № 57 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Мета: сформувати в учнів свідоме розуміння змісту та доведення теореми, що містить формули доповнення, а також наслідку з неї; домогтися засвоєння учнями способу обчислення та значень тригонометричних функцій кутів 30°, 45° і 60°. Закріпити знання вивчених формул та сформувати вміння їх застосовувати […]...
- Формули в органічній хімії ХІМІЯ – Комплексна підготовка до зовнішнього незалежного оцінювання РОЗДІЛ III. ОРГАНІЧНА ХІМІЯ 10. Теоретичні основи органічної хімії 10.3. Формули в органічній хімії В органічній хімії використовують декілька типів формул. 1. Електронні формули схематично відображують механізм утворення ковалентного хімічного зв’язку в молекулах: 2. Молекулярні формули показують якісний і кількісний склад речовини. У свою чергу, молекулярні формули […]...
- Дії з дробами Формули й таблиці МАТЕМАТИКА Дії з дробами...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Лабораторна робота № 8. Внутрішня будова листка у зв’язку з його функціями Розділ І. РОСЛИНИ Тема 1. Будова та життєдіяльність рослин (на прикладі покрито-насінної дводольної рослини) УРОК 12* Тема. Лабораторна робота № 8. Внутрішня будова листка у зв’язку з його функціями Мета. Ознайомитися з внутрішньою будовою листка та його структурними елементами у зв’язку з функціями, які вони виконують. Обладнання: листки кімнатних рослин, мікропрепарат “Поперечний розріз листка”, мікроскоп, […]...
- Лабораторна робота № 3. Внутрішня будова кореня у зв’язку з його функціями Розділ І. РОСЛИНИ Тема 1. Будова та життєдіяльність рослин (на прикладі покрито-насінної дводольної рослини) УРОК 8 * Тема. Лабораторна робота № 3. Внутрішня будова кореня у зв’язку з його функціями Мета. Розширити знання учнів про анатомічну будову кореня у зв’язку із функціями, що вони виконують. Основні поняття і терміни: кореневий чохлик, зона ділення, зона росту, […]...
- Тригонометричні функції числового аргументу УРОК 7 Тема. Тригонометричні функції числового аргументу Мета уроку: Формування поняття тригонометричних функцій числового аргументу; вивчення значень тригонометричних функцій деяких чисел (кутів), зміни знаків тригонометричних функцій у координатних чвертях. І. Перевірка домашнього завдання Розв’язування вправ аналогічних до домашніх. 1. Подайте в радіанній мірі кути: А) 5°; б) 1140°; в) -765°; г) 67° 5′. Відповідь: а) […]...
- Хімічні символи і формули ХІМІЯ – Комплексна підготовка до зовнішнього незалежного оцінювання РОЗДІЛ І. ЗАГАЛЬНА ХІМІЯ 1. Основні хімічні поняття. Речовина 1.3. Хімічні символи і формули Кожен хімічний елемент має свій хімічний символ. Символи, як правило, складаються з початкових літер латинських назв хімічних елементів – Н (Hydrogenium), Не (Helium), Li (Lithium) і далі; Be, В, С, N, О, F… […]...
- Формули скороченого множення Математика – Алгебра Многочлен Формули скороченого множення – Формула різниці квадратів. Добуток різниці двох виразів і їх суми дорівнює різниці квадратів цих виразів. – Формула квадрата суми. Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів і плюс квадрат другого виразу. – Формула квадрата різниці. Квадрат різниці двох виразів дорівнює квадрату […]...
« КОЛЯДА