Головна ⇒ 📌Довідник с фізики ⇒ Стаціонарна теплопровідність. Коефіцієнт теплопровідності

Стаціонарна теплопровідність. Коефіцієнт теплопровідності

ФІЗИКА

Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА

Розділ 5 ЯВИЩА ПЕРЕНЕСЕННЯ

5.10. Стаціонарна теплопровідність. Коефіцієнт теплопровідності

Унаслідок теплового руху молекул будь-який переріз в об’ємі, який займає газ, перетинається молекулами. Розглянемо деяку площадку s (рис. 5.9), перпендикулярну до осі х, уздовж якої підтримується стала різниця температур (процес стаціонарний). Припустімо, що температура Т1 більша, ніж Т2 (Т1 >Т2).

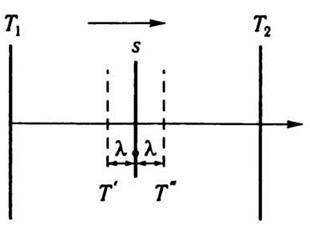
Рис. 5.9

Через площадку s проходять молекули як зліва направо,

так і справа наліво. Якщо при цьому тиск газу в усіх точках один і той самий, то число молекул, що перетинають за 1 с одиницю площі s, зліва і справа має бути однаковим. Проте молекули, що рухаються зліва, несуть із собою більшу енергію, ніж молекули, які надходять до площадки справа, оскільки вони рухаються із зони більш високої температури. Унаслідок цього виникає потік теплоти (зліва направо), який дорівнює різниці енергій, що переносять молекули зліва і справа.

Як відомо, число молекул N1, які перетинають 1 см2 площадки s зліва направо, дорівнює 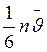. Справа наліво проходить N2 молекул, де це число

також становить. Нагадаємо, що

Стаціонарна теплопровідність. Коефіцієнт теплопровідності

– середня швидкість теплового руху молекул і n – число молекул в одиниці об’єму. Хоча N1 = N2, проте енергії вони несуть різні. Знайдемо спочатку ці енергії.

Молекули, які надходять до площадки s зліва, рухаються до неї з тією самою енергією, яку вони мали після останнього перед площадкою зіткнення. Довжина вільного пробігу в різних молекул різна, але грубо можна прийняти, що молекули, які надходять до площадки s, мали останнє зіткнення на відстані від неї, що дорівнює середній довжині вільного пробігу 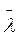. Відповідно до цих міркувань можна вважати, що молекули, які надійшли до площадки зліва, мають середню енергію 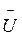1, яка відповідає температурі Т’ у точці на відстані 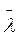від площадки s. Кількість енергії, яку приносять молекули за 1 с до 1 см2 площадки, становить

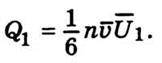
Аналогічно кількість енергії, яку приносять молекули справа до площадки, дорівнює

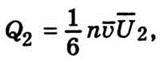
Де 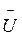2 – середня енергія молекул, яка відповідає температурі Т’ у точці, що лежить від площадки в на відстані 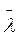справа. Отже, результуюче значення кількості енергії, яка протікає через 1 см2 площадки s за 1 с, становить

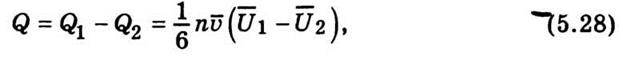
Де 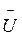1 і 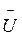2 – середні значення енергії молекул, які відповідають температурам Т’ і Т” у точках, що розміщуються одна від одної на відстані 2.

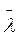Середня енергія однієї молекули 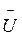пропорційна температурі, її можна виразити через теплоємність газу СV. Середня енергія молекули дорівнює 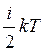, де і – число ступенів вільності. Молярна теплоємність газу 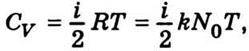де N0 – число Авогадро; k – стала Больцмана. Тому

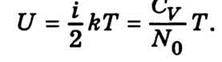
Отже, вираз для теплоти ф можна записати у такому вигляді:

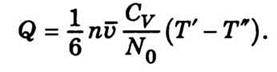
Різницю температур Т’-Т” між точками, які лежать по обидва боки площадки в на відстані 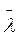від неї, можна визначити із значення градієнта температури:

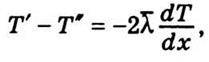
Оскільки градієнт температури 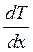є зміною температури на одиницю довжини. Знак мінус вказує на те, що зростанню х відповідає зменшення Т. Звідси

Зіставляючи співвідношення (5.29) і (5.24), дістанемо вираз для коефіцієнта теплопровідності:

Якщо врахувати, що 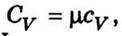де cV – питома теплоємність, а μ – молярна маса і μ/N0 = m – маса однієї молекули, то формулу (5.30) можна записати у вигляді

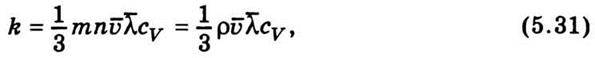
Де, як уже відомо, ρ = mn (добуток маси молекули на число молекул в одиниці об’єму).

Вирази (5.30) і (5.31) дають лише наближене значення коефіцієнта теплопровідності газу, оскільки чисельний множник у цих формулах залежить від припущень, зроблених під час розрахунків, і лише приблизно дорівнює 1/3. Точно розрахувати цей множник досить важко.