Тематична контрольна робота № 6
УРОК № 59
Тема. Тематична контрольна робота № 6
Мета уроку: перевірка навчальних досягнень учнів з теми “Початкові відомості зі стереометрії”.
Тип уроку: контроль навчальних досягнень учнів.
Вимоги до рівня підготовки учнів: застосовують означення та властивості геометричних фігур при розв’язуванні задач.
Хід уроку
І. Тематичне оцінювання № 6
Тематичне оцінювання № 6 можна провести у вигляді тематичної контрольної роботи. Наводимо текст контрольної роботи. Кожна правильна відповідь оцінюється в 3 бали.
Варіант
1. В основі піраміди лежить квадрат зі стороною 5 см. Обчисліть об’єм піраміди, якщо її висота дорівнює 6 см. 2. В основі правильної призми лежить трикутник із стороною 4 см, а її бічне ребро дорівнює 10 см. Знайдіть площу бічної поверхні цієї призми. 3. Діагональ осьового перерізу циліндра дорівнює 10 см, а його висота – 6 см. Знайдіть площу поверхні та об’єм циліндра. 4. Твірна конуса дорівнює l і утворює з висотою конуса кут?. Знайдіть площу бічної поверхні та об’єм конуса.
Варіант 2
1. В основі прямої трикутної призми лежить прямокутний трикутник з катетами 3 см і 4 см. Обчисліть об’єм призми,
Варіант 3
1. Висота циліндра дорівнює 6 см, а діаметр основи – 8 см. Знайдіть площу бічної поверхні циліндра. 2. Твірна конуса дорівнює 5 см, а його висота – 4 см. Знайдіть об’єм конуса. 3. В основі правильної піраміди лежить квадрат зі стороною 10 см. Висота піраміди дорівнює 12 см. Знайдіть площу поверхні та об’єм піраміди. 4. Діагональ бічної грані правильної трикутної призми дорівнює l і утворює з бічним ребром кут?. Знайдіть площу бічної. поверхні та об’єм призми.
Варіант 4
1. Діаметр основи конуса дорівнює 6 см, а твірна – 5 см. Знайдіть площу бічної поверхні конуса. 2. Діагональ осьового перерізу циліндра дорівнює 13 см, а його висота 5 см. Знайдіть об’єм циліндра. 3. В основі прямої призми лежить прямокутний трикутник з катетами 6 см і 8 см. Бічне ребро дорівнює найбільшому ребру основи. Знайдіть площу поверхні та об’єм призми. 4. Бічне ребро правильної чотирикутної піраміди дорівнює l і утворює з висотою кут?. Знайдіть площу бічної поверхні та об’єм піраміди.
Відповіді та розв’язання до завдань тематичної контрольної роботи
Варіант 1
1. V = 
Sосн Н. Оскільки Sосн = 52 = 25(см2), Н = 6 см, то V = • 25 • 6 = 50 (см3). Відповідь. 50см3.
2. Sбічн = P • H. Оскільки Р = 3 • 4 = 12 (см), Н = 10 см, то Sбічн = 12 • 10 = 120 (см2). Відповідь. 120 см2.
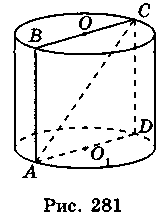
3. Нехай АС = 10 см, CD = 6 см (рис. 281), тоді з трикутника ACD маємо:
AD =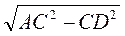 
= 
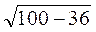= 8 (см), отже, АО = 
AD =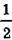 
• 8 = 4 (см).
S = Sбічн + 2Sосн = 2n • AО1 • CD + 2n • AO12 = 2n • 4 • 6 + 2n • 42 = 48n + 32n = 80n (см2). V = nАО12 • CD = n • 42 • 6 = 96n (см3).
Відповідь. 80n см2, 96n см3.
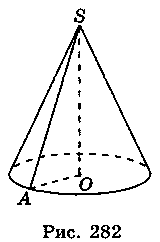
4. Нехай AS = l, 
ASO = ? (рис. 282). Тоді із трикутника ASO маємо:
АО = AS sinASO = l sin?, SO = AS cosASO = lcos?.
Sбічн = n • AO • AS = n l sin? • l = nl2sin?.
V = N • AO2 • SO = Nl2 sin2? l cos? = 
.
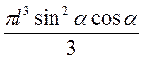Відповідь. nl2sin?, .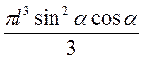
Варіант 2
1. V = Sосн? H. Оскільки S = ? 3 ? 4 = 6 (см2), Н = 5 см, то V = 6 ? 5 = 30 (см3). Відповідь. 30 см3.
2. S = 4 ? S? = 4 ?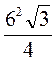 
= 36
(см2). Відповідь. 36 см2.
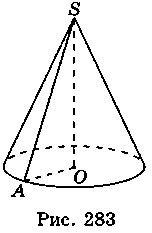
3. Нехай AО = 6 см, SO = 8 см (рис. 283), тоді із трикутника SAO маємо:
AS =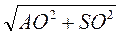 
= 
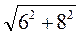= 10 (см).
Sкон = Sосн + Sбічн = n? AО2 + n? AO? AS = n? 62 + n? 6 ? 10 = 96n (см2).
V = N? AO2 ? SO = N? 62 ? 8 = 96n (см3). Відповідь. 96n см2 , 96n см3.
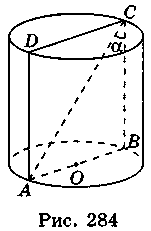
4. Нехай AC = l, ACB = ? (рис. 284). Тоді із трикутника АСВ маємо:
СВ = AC cosАСВ = l cos?, АВ = AC sinАСВ = l sin?,
Звідси АО = АВ = L sin?.
Sбічн = 2n? АО? СВ = 2 ? n? Lsin? ? lcos? = nl2 sin? cos?.
V = n? AO2 ? CB = n?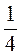 
L2 sin2? ? lcos? = 
.
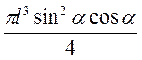Відповідь. nl2 sin? cos?, .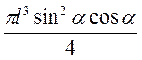
Варіант 3
1. Sбічн = 2nRH. Оскільки 2R = 8 см, H = 6 см, то Sбічн = n? 8 ? 6 = 48n (см2).
Відповідь. 48n см2.
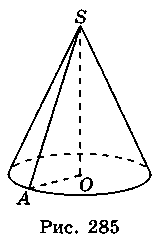
2. Нехай AS = 5 см, SO = 4 см (рис. 285). Тоді із трикутника SAO маємо:
АО =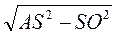 
= 
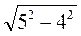= 3 (см).
V =N? AО2 ? SO = N? 9 ? 4 = 12n (см3). Відповідь. 12n см3.
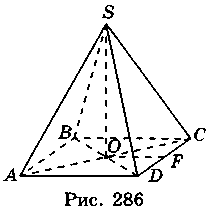
3. Нехай SABCD – правильна піраміда, АВ = 10 см, SO = 12 см (рис. 286). Проведемо SF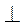 
CD, тоді DF = CF = 5 см. Із прямокутного трикутника SOF маємо: SF = 
= 
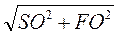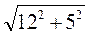=13 (см).
S = Sосн + Sбічн = AB2 + 2 ? AB? SF = 102 + 2 ? 10 ? 13 = 360 (см2).
V = AB2 ? SO = ? 100 ? 12 = 400 (см3). Відповідь. 360 см2, 400 см3.
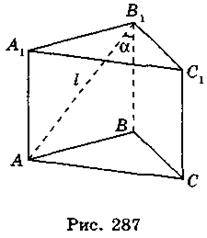
4. Нехай ABCA1В1C1 – пряма призма, у якій АВ1 = l, AB1B = ? (рис. 287). Із прямокутного трикутника АВ1В маємо: АВ = АВ1 sinАB1В = l sin?, BB1 = АВ1 cosAB1B = l cos?.
Sбічн = 3 ? АВ? ВВ1 = 3 ? l sin? ? l cos? = 3l2sin? cos?.
V = Sосн? BB1 =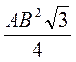 
? BB1= 
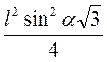? 2cos? = 
.
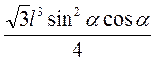Відповідь. 3l2 sin? cos?, .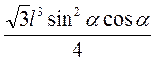
Варіант 4
1. Sбічн = nRl. Оскільки R =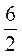 
= 3 (см), l = 5 см. то Sбічн = n? 3 ? 5 = 15? (см2).
Відповідь. 15n см2.
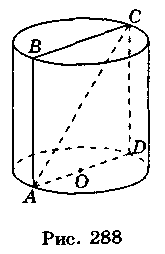
2. Нехай AC = 13 см, CD = 5 см (рис. 288). Тоді із прямокутного трикутника ACD маємо: AD =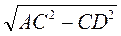 
= 
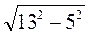= 12 (см),
АО = AD = 6 (см). V = n? АО2 ? СD = n? 62 ? 5 = 180n (см3).
Відповідь. 180n см3.
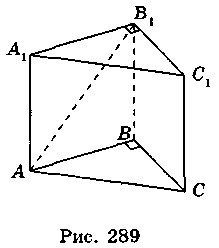
3. Нехай АВСA1В1C1 – пряма призма, B = 90°, AB = 6 см, ВС = 8 см, АА1 = АС (рис. 289). Із трикутного трикутника ABC маємо:
АС =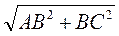 
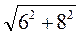= = 10 (см).
S = 2Sосн + Sбічн = 6 ? 8 + 24 ? 10 = 48 + 240 = 288 (см2).
V = Sосн? AA1 = ? AB? BC? AA1 = ? 6 ? 8 ? 10 = 240(см3).
Відповідь. 288 см2, 240 см3.
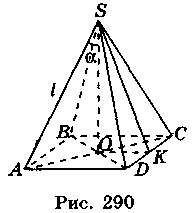
4. Нехай SABCD – правильна піраміда, AS = l, ASO = ? (рис. 290). Із прямокутного, трикутника SOA маємо:
АО = AS sinASO = l sin?, SO = AS cosa ASO = l cos?.
Тоді AB = DC = AO
= L sin?.
Проведемо SK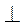SC, тоді SK = 
= 
= 
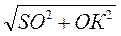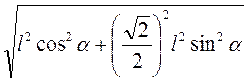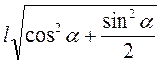. Sбічн = 2 ? DC? SK = 2Lsin? ? l?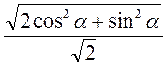 
= 2l2 sin? 
.
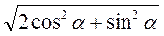V = AB2 ? SO = ? 2l2sin2? ? lcos? = 
.
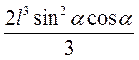Відповідь. 2l2sin?, .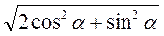
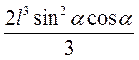Тематичне оцінювання № 6 можна провести у вигляді тесту.
Тестова робота
Кожне завдання І та II рівнів оцінюється 1 балом, III рівня – 2 балами, IV рівня – 3 балами. При оцінюванні враховуються тільки ті шість із виконаних завдань, яким відповідає найбільша кількість балів. Якщо учень набрав у сумі нецілу кількість балів, результат округлюється в бік збільшення. Якщо учень набрав більше 12 балів, він отримує 12 балів.
Варіант 1
I рівень
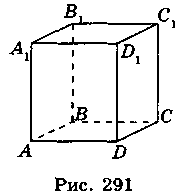
1. На рис. 291 зображено куб ABCDA1B1C1D1. Якій з указаних прямих паралельна пряма ВС?
А DС1 Б АА1 В A1D1
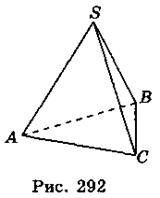
2. На рис. 292 зображено піраміду SABC. Якій із указаних прямих мимобіжна пряма SB?
A. AS; Б. АС; В. АВ.
3. Укажіть, які з наведених тверджень є правильними.
А. Трикутна піраміда має три грані;
Б. Трикутна піраміда має чотири ребра;
В. Протилежні ребра трикутної піраміди не перетинаються.
II рівень
4. Радіус кулі дорівнює 6 см. Знайдіть площу поверхні кулі.
А. 144n см2; Б. 288n см2; В. 576n см2.
5. Кожне ребро правильної трикутної призми дорівнює 6 см. Знайдіть об’єм призми.
А. 9(см3); Б. 12(см3); В. 36(см3).
6. Радіус основи конуса дорівнює 3 см, а твірна – 5 см. Знайдіть висоту конуса.
А. 3 см; Б. 4 см; В. 5 см.
III рівень
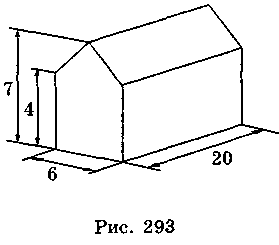
7. Скирта сіна має форму прямої призми з п’ятикутною основою (рис. 293). Розміри скирти (у метрах) подано на рисунку. Знайдіть об’єм скирти.
А. 330 м3; Б. 600 м3; В. 660 м3.
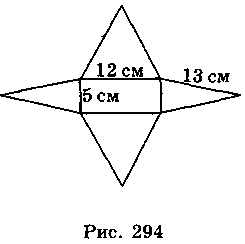
8. На рис. 294 зображено розгортку чотирикутної піраміди, в основі якої лежить прямокутник зі сторонами 5 см і 112 см, а бічні грані якої – рівнобедрені трикутники, з бічною стороною 13 см. Знайдіть об’єм піраміди.
А. 130 см3; Б. 130См3; В. 390 см3.
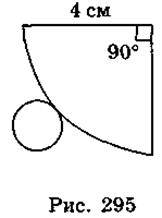
9. На рис. 295 зображено розгортку конуса. Знайдіть площу бічної поверхні конуса.
А. 2n см2; Б. 4n см2; В. 12n см2.
IV рівень
10. Циліндр утворено при обертанні прямокутника навколо сторони, яка утворює з діагоналлю а прямокутника кут?. Знайдіть об’єм циліндра.
A. nd3 sin? cos?;
Б. nd3 sin? cos?;
В. nd3 sin? cos?.
11. В основі прямої призми лежить квадрат. Діагональ призми дорівнює d і утворює з бічним ребром кут?. Знайдіть об’єм призми.
A. D3 sin2?;
Б. D3 sin2? cos?;
B. D3 sin2? cos?.
12. В основі піраміди лежить ромб зі стороною l і гострим кутом?. Висота піраміди дорівнює Н, основа висоти піраміди є точкою перетину діагоналей ромба. Знайдіть об’єм піраміди.
A. Hl2 sin?;
Б. H2l sin?;
В. Нl2 cos?.
Варіант 2
І рівень
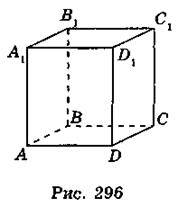
1. На рис. 296 зображено куб ABCDA1B1C1D1. Якій із указаних прямих паралельна пряма АВ?
A. DC1; Б. D1С1; В. CC1.
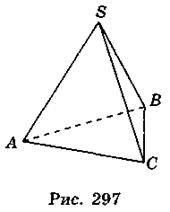
2. На рис. 297 зображено піраміду SABC. Якій із указаних прямих мимобіжна пряма АВ?
A. SA; Б. SB; В. SC.
3. Укажіть, які з наведених тверджень є правильними.
А. Куб має шість ребер;
Б. Усі ребра куба рівні;
В. Куб має дванадцять вершин.
II рівень
4. Радіус кулі дорівнює 6 см. Знайдіть об’єм кулі.
А. 144n см3; Б. 288n см3; В. 576n см3.
5. Кожне ребро трикутної піраміди дорівнює 6 см. Знайдіть площу поверхні піраміди.
А. 9 см2; Б. 36См2; В. 72См2.
6. Радіус основи циліндра дорівнює 3 см, а висота циліндра 4 см. Знайдіть площу бічної поверхні циліндра.
А. 9n см2; Б. 18n см2; В. 24n см2.
III рівень
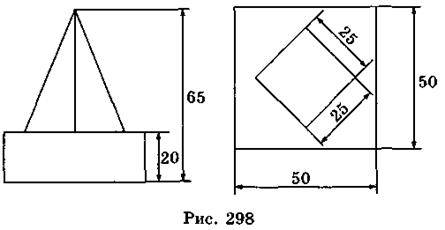
7. 7. На рис. 298 зображено дві проекції деталі (вигляд спереду та зверху). Розміри подано в міліметрах. Знайдіть об’єм деталі.
А. 50 см3; Б. 53,125 см3; В. 60 см3.
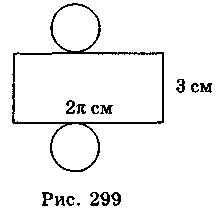
8. На рис. 299 зображено розгортку циліндра. Знайдіть об’єм циліндра.
А. 3n см3; Б. 6n см3; В. 18n см3.
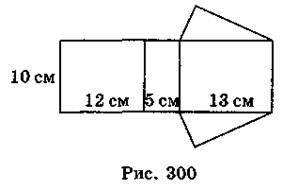
9. На рис. 300 зображено розгортку прямої трикутної призми. Знайдіть площу поверхні призми.
А. 600 см2; Б. 300 см2; В. 360 см2.
IV рівень
10. Конус утворено при обертанні прямокутного трикутника навколо катета, який дорівнює а і утворює кут? з гіпотенузою. Знайдіть об’єм конуса.
А.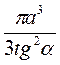 
; Б. Na3tg2?; В. Na3sin2?.
В основі прямої призми лежить прямокутний трикутник з гіпотенузою с і гострим кутом?. Бічне ребро призми дорівнює найбільшій стороні основи призми. Знайдіть об’єм призми.
A. C3 sin? cos?;
Б. С3 sin? cos?;
B. C3 sin? cos2?.
11. В основі піраміди лежить рівнобедрений трикутник з бічною стороною l і кутом при вершині?. Висота піраміди дорівнює Н, основа висоти піраміди – центр кола, описаного навколо основи піраміди. Знайдіть об’єм піраміди.
A.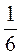 
H2l sin?;
Б. 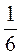Hl2 sin2?;
В. 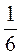Нl2 sin?.
Відповіді до завдань тестової роботи
Рівень | Номер завдання | Варіант 1 | Варіант 2 |
І | 1 | В | Б |
2 | Б | В | |
3 | В | Б | |
II | 4 | А | Б |
5 | В | Б | |
6 | Б | В | |
III | 7 | В | Б |
8 | Б | А | |
9 | Б | В | |
IV | 10 | В | Б |
11 | Б | А | |
12 | А | В |
II. Домашнє завдання
Якщо в класі виконувалася тематична контрольна робота № 5, то вдома можна запропонувати виконати тест, і навпаки.
III. Підбиття підсумків уроку
З’ясувати, які завдання викликали труднощі в учнів, та відповісти на запитання учнів.
(1 votes, average: 5.00 out of 5)
Loading...