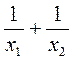Теорема Вієта
Урок № 53
Тема. Теорема Вієта
Мета: закріпити знання учнів щодо змісту теореми Вієта для зведеного квадратного рівняння та для квадратного рівняння загального виду; вдосконалити вміння відтворювати вивчені твердження, використовувати їх для розв’язування завдань, передбачених програмою з математики.
Тип уроку: застосування знань та вмінь.
Наочність та обладнання: опорний конспект “Теорема Вієта”.
Хід уроку
I. Організаційний етан
II. Перевірка домашнього завдання
На цьому етапі уроку проводимо гру “Вірю
III. Формулювання мети і завдань уроку
Формулюємо проблему: як знайти значення виразу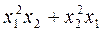 
, де х1 і х2 – корені даного квадратного рівняння (не розв’язуючи рівняння)? Пошук відповіді на це запитання і вивчення сфери застосування теореми Вієта та теореми, оберненої до неї (вдосконалення вмінь), – основна мета уроку.
IV. Актуалізація опорних знань та вмінь
Виконання усних вправ
1. Замініть рівняння рівносильним йому зведеним квадратним рівняння:
А) 3х2 – 6х – 9 = 0;
Б) 2у2 + у – 7 = 0;
В)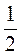 
Х2 – 3х + 1,5 = 0
Та знайдіть суму і добуток
2. Наведіть приклад квадратного рівняння, в якого:
А) один корінь дорівнює нулю, а другий – не дорівнює нулю;
Б) обидва корені дорівнюють нулю;
В) немає дійсних коренів;
Г) корені – протилежні ірраціональні числа.
3. Один із коренів квадратного рівняння х2 + 4х – 21 = 0 дорівнює -7. Знайдіть другий корінь. (Розв’язати задачу різними способами).
V. Відпрацювання вмінь
Виконання письмових вправ
Зміст письмових завдань, пропонованих до розв’язування на уроці, може бути таким:
1. Знайти невідомий корінь та невідомий коефіцієнт квадратного (зведеного та загального виду) рівняння, якщо відомий другий корінь та два інші коефіцієнти.
1) Знайдіть коефіцієнти р і q зведеного квадратного рівняння х2 + рх + q = 0, якщо його коренями є числа 5 і – 2; 2 і -6.
2) Різниця коренів рівняння 3х2 + bх + 10 = 0 дорівнює 4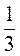
. Знайдіть b.
3) Один із коренів рівняння 5х2 – 12х + с = 0 у 3 рази більше від другого. Знайдіть с.
2. Не розв’язуючи рівняння, знайти значення виразу, що містить його корені х1 і х2.
1) Знайдіть значення виразу (х1 + х2)2 – 3x1x2, якщо х1 і х2 – корені рівняння:
А) х2 – 7х + 9 = 0; б) 3х2 – 7х + 2 = 0.
2) Знайдіть |x1 – х2|, якщо х1 і х2 – корені рівняння: а) х2 – 5х – 14 = 0; б) 2х2 – х – 1 = 0.
3) Числа х1 і х2 – корені рівняння 10х2 + 3х – 4 = 0. Не розв’язуючи рівняння, знайдіть суму квадратів його коренів.
4) Виразіть через р і q суму квадратів коренів рівняння х2 + рх + q = 0.
3. Скласти квадратне рівняння, корені якого більші (менші) від коренів даного рівняння в певну кількість разів.
4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Доведіть, що рівняння 5х2 – 3х – а2 – 2 = 0 при будь-якому значенні а має корені різних знаків.
2) Один із коренів рівняння 4х2 + bх + с = 0 дорівнює 0,5, а другий – вільному члену. Знайдіть b і с.
3) Відомо, що коефіцієнти b і с рівняння х2 + bx + c = 0, де с? 0, є його коренями. Знайдіть b і с.
5. На повторення: розв’язати квадратні рівняння, визначивши попередньо їх вид.
@ Вправи, винесені на урок, мають на меті сприяти закріпленню змісту теореми Вієта та оберненої до неї теореми, відпрацювання навичок використання вивченої теорії в стандартних та нестандартних ситуаціях, повторенню матеріалу та поновленню вмінь розв’язувати квадратні рівняння різних видів відповідними способами.
VI. Підсумки уроку
Самостійна робота 12
Варіант 1 | Варіант 2 |
1. Не розв’язуючи рівняння, знайдіть суму і добуток його коренів: | |
А) х2 + 17х – 38 = 0; б) 3х2 + 8х – 15 = 0 | А) х2 – 17х – 38 = 0; б) 5х2 + 4х – 1 = 0 |
2. Число 8 – корінь рівняння х2 + рх – 16 = 0. Знайдіть р і другий корінь рівняння | 2. Число -12 – корінь рівняння х2 + 15х + q = 0. Знайдіть q і другий корінь рівняння |
3. Числа х1 і х2 – корені рівняння 2х2 – 3х + 1 = 0. Знайдіть значення виразу | 3. Числа х1 і х2 – корені рівняння 2х2 – 5х – 6 = 0. Не розв’язуючи рівняння, знайдіть значення виразу |
VII. Домашнє завдання
1. Повторити зміст і схеми доведення теореми Вієта та оберненої теореми.
2. Розв’язати вправи на застосування вивчених теорем та способів дій.
3. На повторення: означення, класифікація та способи розв’язання квадратних рівнянь різного виду.
(1 votes, average: 5.00 out of 5)
Loading...