Теореми
§ 2. Трикутники
11. Теореми
269.
Теорема | Умова | Висновок |
4.1 | Кути АОС і СОВ – суміжні | ∠AOC + ∠COB = 180° |
8.2 | X належить серединному перпендикуляру відрізка AB | ХА = ХВ |
9.1 | ?ABC – рівнобедрений з основою АС | 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою |
10.3 | Два кути трикутника ABC рівні | ?ABC – рівнобедрений |
11.2 | Точка | X належить серединному перпендикуляру відрізка AB |
270. 1) Теорема – властивості: 4.1; 8.2; 9.1; 11.2.
2) Теореми – ознаки: 10.3.
271. 1) Якщо кути трикутника рівні, то він рівносторонній (пряме і обернене твердження є правильними).
2) Якщо бісектриси двох кутів є доповняльними променями, то ці кути вертикальні (пряме твердження є правильним, а обернене – хибним).
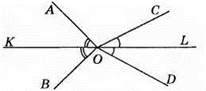
3) Якщо два кути суміжні, то кут між їхніми бісектрисами прямий (пряме твердження є хибним, а обернене – правильним).
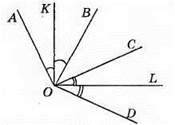
4) Якщо два трикутники
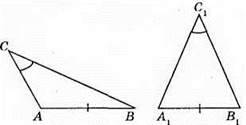
272. 1) Якщо AB + ВС = АС, то точка В лежить між точками Я і С (пряме і обернене твердження є правильними).
2) Якщо периметри двох трикутників не рівні, то ці трикутники не рівні (пряме твердження є хибним, а обернене – правильним).
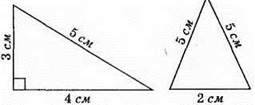
3) Якщо кут є тупим, то його градусна міра більша за 90° (пряме твердження є хибним, а обернене – правильним).
273. 1) Відрізок АВ не перетинає пряму m;
2) градусна міра кута ABC не більша за 40°;
3) обидва суміжні кути більші за 90°;
4) промені ОА і OB є доповняльними;
5) відрізок має більше одної середини або не має жодної середини.
274. 1) Кут ABC є прямим;
2) трикутник МКЕ не є рівнобедреним;
3) через точку на даній прямій можна провести більше одної прямої, перпендикулярної даній, або не можна провести жодної прямої, перпендикулярної даній.
275. Припустимо, що трикутник є рівнобедреним. Тоді висота, проведена до основи, і бісектриса трикутника, проведена із вершини, протилежної до основи, збігається, а це суперечить умові. Отже, трикутник не є рівнобедреним.
276. Припустимо, що медіана BD є висотою трикутника ABC, тоді AB = ВС, що суперечить умові. Отже, медіана BD трикутника ABC не є його висотою.
277. Припустимо, що кути вертикальні, тоді вони рівні, що суперечить умові. Отже, дані кути не можуть бути вертикальними.
278. Припустимо, що обидва кути менші за 90°, тоді їх сума не дорівнює 180°, що суперечить теоремі про суміжні кути. Отже, з двох суміжних кутів хоча б один не менший від 90°.
279. Якщо у двох рівнобедрених трикутників бічні сторони рівні та медіани, проведені до бічних сторін, рівні, то ці трикутники рівні. Або, якщо бічна сторона і медіана, проведена до цієї сторони одного рівнобедреного трикутника, відповідно дорівнюють бічній стороні І медіані, проведеній до цієї сторони, другого рівнобедреного трикутника, ці трикутники рівні.
Доведення.
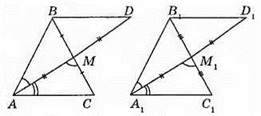
Нехай AB = A1B1, AD = BD, A1D1 = B1D1, CD = C1D1.
?BCD = ?B1C1D1 за трьома сторонами (CВ = C1B1, 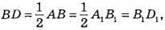 CD = C1D1). Із рівності трикутників випливає, що ∠B = ∠B1. Отже, ?ABC = ?А1В1С1 за першою ознакою (AB = А1В1, BC =B1C1, ∠B = ∠B1).
CD = C1D1). Із рівності трикутників випливає, що ∠B = ∠B1. Отже, ?ABC = ?А1В1С1 за першою ознакою (AB = А1В1, BC =B1C1, ∠B = ∠B1).
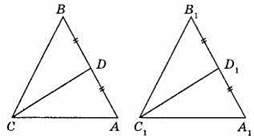
280. Якщо сторона, медіана, проведена до цієї сторони, і кут між медіаною та цією стороною одного трикутника дорівнюють відповідно стороні, медіані, проведеної до цієї сторони, і куту між медіаною та цією стороною другого трикутника, то ці трикутники рівні.
Доведення:
Нехай ВС = В1C1, ВМ = MC, В1М1 = M1C1, AM = A1M1, ∠AMC = ∠A1M1C1.
?АМС = ?A1M1C1 за першою ознакою рівності трикутників (AM = A1M1, MC = M1C1, ∠AMC = ∠A1M1C1). Із рівності цих трикутників випливає, що АС = A1C1, ∠C = ∠C1. Отже, ?ABC = ?A1B1C1 за першою ознакою рівності трикутників (AC = A1C1, ВС = B1C1, ∠C = ∠C1).
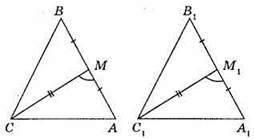
281. Якщо медіана та кути, на які вона розбиває кут, одного трикутника дорівнюють відповідно медіані та кутам, на які вона розбиває кут, другого трикутника, то ці трикутники рівні.
Доведення.
Нехай ABC і А1В1С1 – дані трикутники, відрізки AM і A1M1 – відповідно їх медіани. ∠BAM = ∠B1A1M1, ∠CAM = ∠C1A1M1. На продовженнях відрізків AM і А1М1 за точки М і М1 відкладемо відрізки відповідно MD = МА, M1D1 = M1A1.
?АМС = ?DMB за першою ознакою рівності (AM = MD, MC = ВМ, ∠AMC = ∠DMB). Із рівності трикутників маємо: ∠MAC = ∠BDA, АС = BD.
?A1M1C1 = ?D1M1B1 за першою ознакою рівності (A1M1 = M1D1, M1C1 = В1М1, ∠A1M1C1 = ∠D1M1B1). Із рівності трикутників маємо: ∠M1A1C1 = ∠B1D1A1, A1C1 = B1D1.
?ABD = ?A1B1D1 за другою ознакою рівності (AD = A1D1, ∠BAD = ∠B1A1D1, ∠BDA = ∠B1D1A1). Із рівності трикутників маємо: AB = A1B1, BD = B1D1, тоді, враховуючи, що АС = BD і A1C1 = B1D1,маємо: АС =А1С1.
?ABC = ?A1B1C1 за першою ознакою рівності трикутників (AB = A1B1, АС = A1C1, ∠A = ∠A1).
Вправи для повторення
282. 1) AB + BC = AC; 2) AB + AC > BC; 3) АС + ВС > АВ.
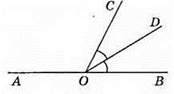
283. На рис. ∠COD = ∠DOB, ∠AOC = 3∠COD. Нехай ∠COD = х°, тоді ∠BOC = 2х°, ∠AOC = 3х°. 2х + 3х = 180, звідси 5х = 180; х = 36. Отже, ∠COB = 36° х 2 = 72°; ∠AOC = 3 x 36° = 108°.
Відповідь: 72°, 108°.
Спостерігайте, рисуйте, конструюйте, фантазуйте
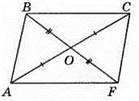
284. Нехай AB = 3 см, ВС = 4 см. Сума довжин горизонтальних відрізків дорівнює подвоєній стороні ВС, а сума довжин вертикальних відрізків – подвоєній довжині сторони AB. Отже, сума довжин усіх відрізків, що містяться всередині прямокутника, дорівнює: 2 х АВ + 2 x BC = 2 x 3 + 2 x 4 = 6 + 8 = 14 (см).
Відповідь: 14 см.
Завдання № 2 “Перевір себе” в текстовій формі
1. Трикутник є гострокутним, якщо кожний його кут менший від прямого.
Правильна відповідь: Б.
2. Якщо висота трикутника йому не належить, то цей трикутник тупокутний.
Правильна відповідь: Б.
3. Два трикутники рівні, якщо дві сторони та кут між ними одного трикутника дорівнюють двом сторонам та куту між ними другого трикутника.
Правильна відповідь: Г.
4. Чотири пари: ?АОВ = ?COD; ?ВОС = ?DOA; ?АВС = ?СDА; ?ABD = ?CDB.
Правильна відповідь: Г.
5. ?АВМ = ?СЕМ (за двома сторонами і кутом між ними), тоді СЕ = AB = 4,2 см.
Правильна відповідь: Б.
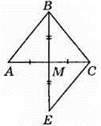
6. Рівносторонній трикутник – окремий вид рівнобедреного трикутника.
Правильна відповідь: В.
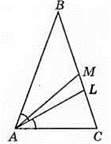
7. Хибне твердження “Якщо медіана і бісектриса, проведені з однієї вершини, не збігаються, то цей трикутник не є рівнобедреним”. (AB = ВС, AM і AL – не співпадають).
Правильна відповідь: Б.
8. Трикутник є рівностороннім, якщо кожна його сторона у три рази менша від його периметра.
Правильна відповідь: Б.
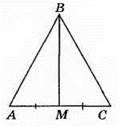
9. Р? ABM + Р? MВС + Р? AВС + 2ВМ, 12 + 12 = 16 + 2ВМ, тоді 2 x ВМ = 24 – 16; 2 х BM = 8; ВМ = 8 : 2; ВМ = 4.
Правильна відповідь: A.
10. Хибним може бути твердження: ∠AXB = ∠AYВ.
Правильна відповідь: В.
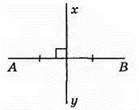
11. Точка X не належить серединному перпендикуляру відрізка AB, якщо ХМ = ХВ.
Правильна відповідь: Б.