Теореми про рівність і подібність трикутників – ТРИКУТНИКИ
Формули й таблиці
МАТЕМАТИКА
ТРИКУТНИКИ
Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин.
Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо один із кутів тупий – трикутник тупокутний.
Трикутник ABC рівнобедрений, якщо його дві сторони рівні (а = с); рівносторонній, якщо
У всякому трикутнику проти більшої сторони лежить більший кут; проти рівних сторін – рівні кути і навпаки.
Рівносторонній трикутник має рівні кути і навпаки: якщо кути трикутника рівні, то він рівносторонній.
У всякому трикутнику сума кутів дорівнює 180°
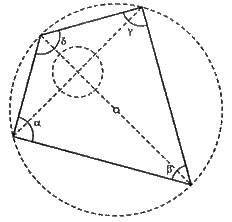
α + β + γ = 180°.
У рівносторонньому трикутнику кожен кут дорівнює 60°.
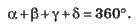
Теореми про рівність i подібність трикутників

Два трикутники подібні, якщо: – їхні сторони відповідно пропорційні; – кути двох трикутників відповідно рівні; – дві сторони одного відповідно пропорційні двом сторонам іншого, кути між ними рівні | Прямокутні трикутники подібні, якщо гіпотенуза й катет одного трикутника пропорційні гіпотенузі й катету іншого |
Трикутники рівні, якщо – сторони одного трикутника відповідно рівні сторонам другого; – відповідно рівні дві сторони й кут між ними; – рівні одна сторона і прилеглі до неї кути 1-го трикутника зі стороною й кутами іншого трикутника. |
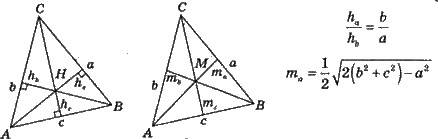
Усяка сторона трикутника менша від суми й більша від різниці двох інших сторін: А < с + b; а > с – b | Висота трикутника – перпендикуляр, опущений з будь-якої вершини трикутника на протилежну сторону або на її продовження |
Точка перетину трьох висот трикутника називається ортоцентром. У тупокутному трикутнику ортоцентр лежить поза трикутником, у прямокутному співпадає з вершиною прямого кута | Медіаною трикутника називається відрізок, що сполучає будь-яку вершину трикутника із серединою протилежної сторони. Три медіани трикутника перетинаються в одній точці (завжди у трикутнику), що є центром ваги (мас) трикутника |
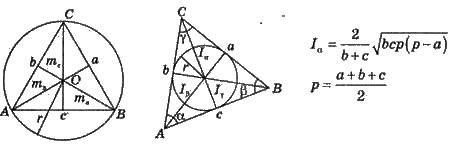
Бісектрисою трикутника називається відрізок бісектриси будь-якого кута від вершини до перетину із протилежною стороною | Три бісектриси трикутника перетинаються в одній точці (завжди усередині трикутника), що є центром вписаного кола |
Бісектриса ділить протилежну сторону на частини, пропорційні прилеглим до неї сторонам | Бісектриса ділить кут навпіл. Висота опускається на протилежну сторону під прямим кутом |
Медіана ділить трикутник на два рівновеликих. Медіана ділить протилежну сторону навпіл | |
Середній перпендикуляр до відрізка – пряма, яка проходить через середину відрізка перпендикулярно до нього | |
Три середніх перпендикуляри до сторін трикутника перетинаються в одній точці, що є центром описаного навколо трикутника кола |