ТОТОЖНІСТЬ
РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ
&4. ТОТОЖНІСТЬ
Ви знаєте, що два вирази зі змінними можуть бути тотожно рівними. Наприклад, такими є пари виразів 3а – а і 2а, 3xy ∙ (- 5z)і – 15xyz, 55nm: 11 i 5nm для будь-яких значень змінних, що входять до них. Якщо в кожній із цих пар вирази поєднати знаком “=”, то дістанемо особливі рівності – тотожності, а саме: 3a – а = 2а, 3ху ∙ (-5z) = -15xyz, 55nm : 11 = 5 nm.
Запам’ятайте!
Рівність, ліва і права частини якої є тотожно рівними виразами, називається тотожністю.
Крім тотожностей зі змінними, вам вже зустрічалися
1 + 1 + 1 + 1 = 4, 2 ∙ 2 ∙ 2 ∙ 2 = 24, 3 ∙ (7 – 5) = 3 ∙ 2.
Кожна тотожність стверджує, що вирази в її лівій і правій частинах є тотожно рівними, тобто їх відповідні значення дорівнюють одне одному для кожного значення їх змінних. Якщо не відомо, чи є тотожно рівними вирази в лівій і правій частинах певної рівності, тоді цю рівність перевіряють на правильність, тобто доводять тотожність або спростовують її.
Довести тотожність – означає довести тотожну рівність її лівої і правої частин. Для доведення тотожностей використовують тотожні перетворення виразів.
Розпочинають доведення
3 а д а ч а 1 . Чи є тотожністю рівність (а -1) ∙ а : (а – 1) = а?
Розв’язання. ОДЗ-1: а ≠ 1, ОДЗ-2: а – будь-яке число.
Оскільки ОДЗ змінних виразів у лівій і правій частинах рівності не збігаються, то дана рівність не є тотожністю.
Якщо ОДЗ змінних виразів у лівій і правій частинах рівності збігаються, тоді застосовують один із чотирьох способів доведення тотожностей. Розглянемо приклад.
З а д ач а 2. Доведіть тотожність 3(b + 2) – b = 3b + 5 – (b – 1).
Розв’язання. ОДЗ-1: b – будь-яке число, ОДЗ-2: b – будь-яке число.
Спосіб 1 (перетворення лівої частини рівності).
Перетворимо вираз у лівій частині даної рівності так, щоб він на – ‘ був вигляду виразу в її правій частині: і3(b + 2)- b =
=3b + 6 – b =
= 3b + 5+1- b =
= 3b + 5 – b + 1 =
= 3b + 5 – (b – 1).
Отже, 3b + 5 – (b – 1) = 3b + 5 – (b – 1).
Звідси 3(b + 2) – b = 3b + 5 – (b – 1), що і вимагалося довести.
Спосіб 2 (перетворення правої частини рівності).
Перетворимо вираз у правій частині даної рівності так, щоб він набув вигляду виразу в її лівій частині:
3b + 5 – (b – 1) =
= 3b + 5 – b + 1 =
= 3b + 6 – b =
= 3(b + 2) – b.
Отже, 3(b + 2) – b=3(b + 2) – b.
Звідси 3(b + 2) – b = 3b + 5 – (b – 1), що і вимагалося довести.
Спосіб 3 (перетворення обох частин рівності).
Перетворимо вирази в обох частинах даної рівності так, щоб вони набули одного й того самого вигляду:
3(b + 2) – b= 3b + 5 – (b – 1) =
= 3b + 6 – b = = 3b + 5 – b + 1) =
= 2b + 6. =2b + 6
Отже, 2b + 6 = 2b + 6.
Звідси 3(b + 2) – b = 3b + 5 – (b -1), що і вимагалося довести.
Спосіб 4 (різницеве порівняння). Перевіримо, чи дорівнює нулю різниця виразів у лівій і правій частинах даної рівності:
3(b + 2) – b – (3b + 5 – (b – 1)) =
= 3b + 6 – b – (3b + 5 – b + 1) =
= 2b + 6 – (2b + 6) =
= 2b + 6 – 2b – 6 = 0.
Звідси 3(b + 2) – b = 3b + 5 – (b – 1), що і вимагалося довести.
– Чи можна спростувати тотожність, не перетворюючи виразів у її лівій і правій частинах? Так. Розглянемо приклад.
З а д а ч а З. Чи є тотожністю рівність 0 ∙ х = х?
Розв’язання. ОДЗ-1: х – будь-яке число, ОДЗ-2: х – будь – яке число. Перевіримо, чи справджується дана рівність, наприклад, для х = 1. Підставивши це значення х у вирази лівої і правої частин рівності, отримаємо, що вони набувають різних значень: 0-1≠1, або 0≠1. Отже, дана рівність не є тотожністю.
Зверніть увагу:
Щоб спростувати правильність рівності зі змінними, достатньо дібрати лише один набір значень змінних, за яких ліва і права її частини набувають різних значень.
Дізнайтеся більше
Доведення вважають єдиним способом встановлення істини в математиці. Проте так було не відразу. Спочатку в єгипетській
І вавилонській математиці обчислювальні формули та математичні факти вгадувались, а потім експериментально перевірялись. Це вважали доказом їх істинності.
Необхідність доведення обгрунтував давньогрецький математик Евклід (III ст. до н. е ). Він вважав, що доведення мають бути логічними висновками з аксіом – тверджень, що приймають без доведення. У результаті з’явилися знамениті “Начала” Евкліда У 1939 р. виходить багатотомний трактат групи французьких математиків, які взяли для цього псевдонім Ніколя Бурбакі. Ось якою фразою відкривають Бурбакі свій трактат: “Із часів греків говорити “математика” – означає говорити “доведення”. Відтоді математика і доведення – два слова, які вважають майже синонімами.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що таке тотожність?
2. Що означає – довести тотожність?
3. У чому суть способу перетворення лівої частини рівності?
4. Поясніть суть способу перетворення правої частини рівності.
5. У чому суть способу перетворення обох частин рівності?
6. Поясніть суть способу різницевого порівняння.
7. Як спростувати правильність рівності зі змінними?
РОЗВЯЖІТЬ ЗАДАЧІ
132. Чи правильно, що тотожністю може бути:
1) вираз; 2) нерівність; 3) рівність?
133. Чи правильно, що ліва і права частини тотожності мають бути:
1) нерівними виразами;
2) рівними виразами;
3) тотожно рівними виразами?
134. Чи може бути тотожністю рівність, у якої:
1) ОДЗ-1 і ОДЗ-2 не збігаються;
2) ОДЗ-1 і ОДЗ-2 збігаються?
135. Чи є тотожністю числова рівність? Якщо так, наведіть приклад.
136. Чи може бути тотожністю запис:
1) a ∙ 1 – a;
2) 3а – 4a ≠ 5a;
3) a ∙ a – a2 = 0;
4) 2a – 2 = a;
5) 4а – 2а + а = 3а,
6) 
= 
?
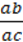137. Чи може бути тотожністю запис:
1) b + 2 > 0;
2) b ∙ 
– 
;
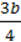3) -3b + 3b = 0?
4) 4b – 5b + 6b = 5b;
138. Чи правильно, що рівність 12 – (5 – 9) = 16 є тотожністю? Відповідь поясніть.
139. Що треба вставити замість *, щоб отримати тотожність:
1)2b + b = *,
2) b ∙ * = 0;
3) b ∙ b ∙ b = *;
4) 2b + * = 0;
5) 5(8b – 6) = *;
6) 
= 
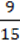140. Що треба вставити замість *, щоб отримати тотожність:
1)5a – * = 2a; 3) 4 ∙ (a – 2) = *;
2) a ∙ * = 1; 4) 7a + * = 0?
141. Доведіть тотожність за допомогою способу перетворення лівої частини рівності:
1) 10a – (6a – 9b) = 4a + 9b;
2) (0,7n – 0,6m) – 2(0,4n – 0,3m) = -0,1n.
142. Доведіть тотожність за допомогою способу перетворення лівої частини рівності: (17а – 6b) + 4(-5а + 4b) = -3а + 10b.
143. Доведіть тотожність за допомогою способу перетворення правої частини рівності:
1) a = -1
(a-7b) + 2 a – 9b;
2) с – d = 4(d – c) – 5(d – с).
144. Доведіть тотожність за допомогою способу перетворення правої частини рівності: -6c = 0,8(5c – 3d) – 4(2,5c – 0,6d).
145. Доведіть тотожність за допомогою способу перетворення обох частин рівності:
1) 12а – 4(3а – 7b) = (4а + b) – (4а – 27b);
2) 4,5 + (1
N + 2,5m) – 0,5n = 7(m – 
N) + 1
N.
146. Доведіть тотожність за допомогою способу перетворення обох частин рівності:
(2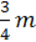
– 10,4n) – 4(
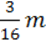– 1,6n) = -2(2n – m).
147. Доведіть тотожність за допомогою способу різницевого порівняння:
1) 4,9а – 4 (а – 0,6b ) = 0,3 (3а + 8b);
2) (p –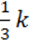 
) – (3p – 
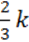) = (k – 2p) – 
.
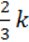148. Доведіть тотожність за допомогою способу різницевого порівняння: 18р – 4(2k + 5p) = –
(16k + 4p).
149. Чи є тотожністю рівність:
1) 5а – 2 = а + (4а – 2);
2) 14(b – b) = 14;
3) (2х – 4у) : 2 = х – 2у;
4) 6 m ∙ (4 + m) : 6mn = (4 + m) : n?
150. Чи є тотожністю рівність:
1) – c + d – 2c + 2 = -3c + 3d;
2) (9k – 6k) : 3k = 3k?
151. Доведіть чи спростуйте тотожність:
1) а(b – с) – b(а – с) + с(а – b) = 0;
2) с(n + m) – с(m – n) = 2n (с + m) – 2mn;
3) 4(p + 2k) – k(8 – 4p) = 4(k – 2p);
4) 1,2с(6 – 2p) = 0,8(9с + 6р) – p(2,4с – 4,8).
152. Доведіть чи спростуйте тотожність:
1) a(b – c – d) + a(b + c + d) = 2ab,
2)-m(n + 4) + n(m + 4) = 4(m – n).
153. Доведіть тотожність 8(а – b) + 6(b – с) – 4(а – с) = 4а -2(b + с) різними способами.
154. Доведіть тотожність 2(n + р) – 4m = 2(-n + m) – 6(m – р) + 4(n – р) різними способами.
155. Доведіть, що значення виразу не залежить від значення змінної:
1) 12x – 5(5 + 3x) + 3(x + 4);
2) 8,5(у + 2) – 1,7 (10 + 5у) -15 > 5;
3) а(b – 4) + b(6 – а) – 2(3b – 2а);
4) 7 – 1M + 6(M – 5N) – 0,5(m – 64n).
156. Доведіть, що значення виразу не залежить від значення змінної:
1) 9(5 – у) + 6(у – 3) – 3(4 – у);
2) m(n – 2,8) + n(4,2 – m) – 1,4(3n – 2m) – 6.
157. Доведіть, що 5а(3b – 2с) + 4b(2с – За) – 7с(-а + b) – bс = 15, якщо а(b – с) = 5.
158. Доведіть, що за будь яких а і b значення виразу 5а + 5b – (4b – 2 – 0,5(2а – 5b – 3(2а – 3b + 2(а + b)))) дорівнює 2.
159. Який вираз треба підставити замість зірочки, щоб отримати тотожність:
1) 2(а + b) – 2 ∙ * =4b;
2) 2(а + b) – 2 ∙ * = 0;
3) 2(а + b) – 2 ∙ * = 4а + 4b;
4) 2(а + b) – 2 ∙ * = 2а + 6b;
5) 2(а + b) – 2 ∙ * =4а – 4b;
6) 2(а + b) – 2 ∙ * = 4b – 2а?
160. Доведіть, що середнє арифметичне трьох послідовних натуральних чисел дорівнює середньому із цих чисел.
161. Доведіть, що середнє арифметичне десяти натуральних чисел не може дорівнювати 5,8.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
162. Сергійко з друзями вирушили в похід до бази відпочинку, яка розташована на відстані 250 км від їх міста. Вони планували спочатку 2 год йти пішки зі швидкістю 5 км/год, а потім 4 год їхати автобусом зі швидкістю 60 км/год. Проте швидкість їх руху під час пішої частини походу становила лише 4 км/год. Якою має бути швидкість автобуса, щоб хлопці вчасно потрапили на базу? Складіть числовий вираз для розв’язування задачі та обчисліть його значення.
163. Одна ділянка землі має форму квадрата зі стороною а, а друга – форму прямокутника, довжина якого 2а. Обидві ділянки огороджені. Яка з ділянок має довшу огорожу, якщо ділянки мають однакову площу? Складіть вираз для знаходження різниці довжин огорожей та знайдіть його значення, якщо а = 80 м.
164. Клієнт поклав у банк n грн. Якою буде сума на його рахунку через 2 роки, якщо банк нараховує 15 % річних?
165. Населення міста становить на сьогодні m тис. жителів та збільшується щороку на 3 %. Яким стане населення міста через 5 років?
ЗАДАЧІ НА ПОВТОРЕННЯ
166. Обчисліть:
1) 34 + 22 ∙ 53;
2) (34 + 22) ∙ 53.
167. Порівняйте значення виразів a2 + b2 і (a + b)2, якщо а = 4, b = – 5.
168. На уроці математики в 7-А класі присутні 30 учнів. Число учнів, які відсутні, становить загальної кількості учнів. Скільки учнів навчається в 7-А класі?
169. На прем’єрному показі нового фільму діти становили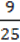 
усіх глядачів. Скільки відсотків від усіх глядачів становили діти?
ПЕРЕВІРТЕ, ЯК ЗАСВОЇЛИ МАТЕРІАЛ
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Що називається числовим виразом; значенням числового виразу?
2. Назвіть дії першого ступеня, другого ступеня, третього ступеня.
3. Який порядок виконання дій у числовому виразі без дужок?
4. У якому порядку треба виконувати дії в числовому виразі з дужками?
5. У якому випадку числовий вираз не має змісту?
6. Який вираз називають виразом зі змінними?
7. Поясніть, як обчислити значення виразу зі змінними.
8. Що таке допустимі значення змінних для виразу зі змінними?
9. Які вирази називаються раціональними; цілими?
10 . Які вирази називаються тотожно рівними?
11. Що таке тотожне перетворення виразу?
12. Для чого використовують тотожні перетворення виразів?
13. Як зводять подібні доданки?
14 . Сформулюйте правила розкриття дужок.
15. Як виносять спільний множник за дужки?
16. Що таке тотожність? Що означає – довести тотожність?
17. У чому полягає суть способу доведення тотожності перетворенням її лівої частини; правої частини?
18. У чому полягає суть способу доведення тотожності перетворенням обох її частин?
19. Поясніть суть способу доведення тотожності способом різницевого порівняння.
ТЕСТОВІ ЗАВДАННЯ
Уважно прочитайте задачі і знайдіть серед запропонованих відповідей правильну. Для виконання тестового завдання потрібно 10-15 хв.
1. Знайдіть значення виразу 10,5 : 5 – (3,4 + 22 ∙ 2,5).
А. 11,3.
Б.-11,3.
В.-13,3.
Г. -18,5.
2 . Винесіть спільний множник за дужки у виразі: 0,4ab – 2ас + 3,6аd.
A. a(0,4b – 2c + 3,6d).
Б. 2a(0,4b – c + 3,6d).
В. 2a(0,2b – с + 1,8d).
Г. 2a(0,2b – c + 3,6d).
3. Спростіть вираз 4,5n + 12,4 – 2n – 1 
N.
А. -1
N + 12,4.
Б. 13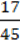 
N.
В. 12,4 – 1N.
Г. 1 N + 12,4
4. Знайдіть значення виразу 2(14а + b) – (3b – 2,8а), якщо а = -0,5 і b = 2 .
А. -7,2.
Б. 7,2.
В. -11,4.
Г.11,4.
5. Яке число треба поставити замість зірочки у рівності * (4,5а – 1B) = -9a + 3
B. щоб отримати тотожність?
A. – 0,2.
Б. 2.
В. -2.
Г. -0,5.
(1 votes, average: 5.00 out of 5)
Loading...