Головна ⇒ 📌ГДЗ з математики ⇒ Трикутник і його елементи

Трикутник і його елементи

Розділ 1. Найпростіші геометричні фігури та їх властивості

§ 9. Трикутник і його елементи

292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони DC і ВС.

293.

Трикутник і його елементи

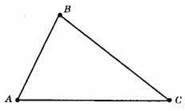
1) Проти кута А лежить сторона ВС, проти кута В лежить сторона АС.

2) Проти сторони AB лежить кут С, проти сторони ВС лежить кут А.

3) До сторони AB прилеглими кутами є ∠A i ∠B.

4) Між сторонами АС і

ВС лежить кут С.

294.

Трикутник і його елементи

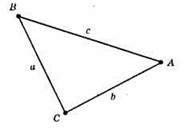
Вершини: В, А, С.

295.

Трикутник і його елементи

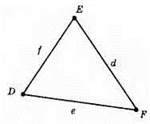
Сторони трикутника: DE, EF, FD. Кути трикутника: ∠Е, ∠F, ∠D.

296. Оскільки 13 < 15 + 14, 15 < 14 + 13, 14 < 13 + 15, то нерівність трикутника виконується.

297. 1) ?BFC. 2) ?AFB і? BFC. 3) ?АВС, ?ABD, ?FBD, ?DBC. 4) ?FBC. 5) ?FBD, ?CBD, ?ABD, ?ABC. 6) ?AFB.

298.

Трикутник і його елементи

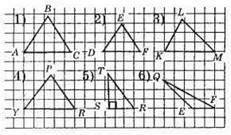
299. Медіана – CL, бісектриса – BN, висота – AM.

300.

Трикутник і його елементи

301.

Трикутник і його елементи

302.

Трикутник і його елементи

303.

Трикутник і його елементи

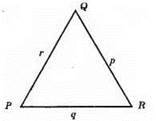
1) Ні, проти сторони PQ лежить кут R.

2) Так.

3) Ні, між сторонами PR і OR лежить

кут R.

4) Так.

304. Мал. 199. Із зображених відрізків не можна утворити трикутник, оскільки не виконується нерівність трикутника, бо 6 см = 3 см + 3 см.

Мал. 200. Із зображених відрізків можна утворити трикутник, оскільки виконується нерівність трикутника, бо 6 см < 4 см + 3 см.

305. 1) Так, бо виконується нерівність трикутника, оскільки 4 см < 2 см + 3 см.

2) Ні, бо не виконується нерівність трикутника, оскільки 13 см = 6 см + 7 см.

3) Так, бо виконується нерівність трикутника, оскільки 9 см < 7 см + 8 см.

306. 1) Різносторонній. 2) Рівносторонній, оскільки 0,3 дм = 30 мм = 3 см. 3) Рівнобедрений, оскільки 0,06 дм = 6 мм ≠ 0,1 см.

307.

Трикутник і його елементи

1) Основа АС, бічні сторони AB і ВС.

2) Основа ВС, бічні сторони AB і АС.

3) Основа АB, бічні сторони АС і ВС.

308. Не можна накреслити рівносторонній трикутник, який не буде рівнобедреним, оскільки у рівностороннього трикутника всі сторони рівні.

309.

α

12 см

20 см

8 см

9 см

β

16 см

21 см

15 см

8 см

С

18 см

29 см

17 см

14 см

Р

46 см

70 см

40 см

31 см

310. Оскільки у рівностороннього трикутника всі сторони рівні, то, щоб знайти сторону рівностороннього трикутника за його периметром, треба периметр поділити на 3.

1) 36 см : 3 = 12 см; 2) 45 см : 3 = 15 см; 3) 72 см : 3 = 24 см.

311. 1) Р = α + 2β = 14 см + 2 х 12 см = 14 см + 24 см = 38 см;

2) P = α + 2β = 16 см + 2 x 17 см = 16 см + 34 см = 50 см;

3) P = α + 2β = 8 см + 2 x 5 см = 8 см + 10 см = 18 см.

312. 1) Прямокутний. 2) Тупокутний. 3) Тупокутний.

313. 1) Прямокутний. 2) Гострокутний. 3) Тупокутний.

314.

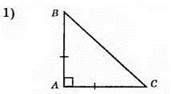
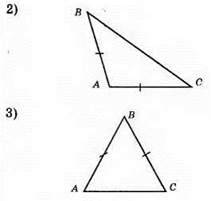
Трикутник і його елементи

Трикутник і його елементи

315. 1) Катети AB і АС, гіпотенуза BC.

2) Катети AB і ВС, гіпотенуза АС.

3) Катети AB і ВС, гіпотенуза АС.

4) Катети AB i АС, гіпотенуза ВС.

316.

Трикутник і його елементи

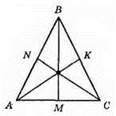
1) AN = BN = AB : 2 = 5 см : 2 = 2,5 см;

AM = CM = AC : 2 = 8 CM ; 2 = 4 см;

BK = CK = BC : 2 = 7 CM : 2 = 3,5 см.

2) AN = BN = 20 : 2 = 10 (см);

AM = CM = BK = CK = 22 : 2 = 11 (см).

3) AN = BN = BK = CK = 10 : 2 = 5 (см);

AM = CM = 16 : 2 = 8 (см).

4) AN = BN = AM = CM = BK = CK = 27 : 2 = 13,5 (см).

317. Бісектриса трикутника – це відрізок бісектриси кута, а бісектриса кута – це промінь.

318.

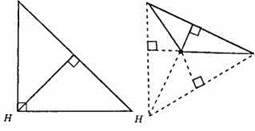
Трикутник і його елементи

Трикутник і його елементи

319.

Трикутник і його елементи

Н – точка перетину висот.

320. 1) Сторони трикутника не можуть бути пропорційні числам 1, 2, 3, оскільки не буде виконуватися нерівність трикутника, бо 3k = k + 2k, де 3k, 2k, k – довжини сторін трикутника.

2) Сторони трикутника можуть бути пропорційні числам 3, 4, 5, оскільки виконується нерівність трикутника, бо 6k < 3k + 4k, де 3k, 4k, 6k – довжини сторін трикутника.

3) Сторони трикутника не можуть бути пропорційні числам 3, 5, 9, оскільки не буде виконуватися нерівність трикутника, бо 9k > 3k + 6k, де 3k, 6k, 9k – довжини сторін трикутника.

321. 1) Якщо сторони трикутника відносяться як 1 : 1 ; 1, то вони рівні. Отже, даний трикутник рівносторонній.

2) Якщо сторони трикутника відносяться як 5 : 12 : 13, то трикутник не має рівних сторін. Отже, даний трикутник різносторонній.

3) Якщо сторони трикутника відносяться як 5 : 5 ; 8, то трикутник має дві рівні сторони. Отже, даний трикутник рівнобедрений.

322. 1) Оскільки α > с і β > с, то α = β, отже, AB – основа рівнобедреного трикутника, ВС і СА – бічні сторони.

2) Оскільки α < β і с < β, то α = с, отже, АС – основа рівнобедреного трикутника, ВА і ВС – бічні сторони.

3) Оскільки α ≠ β і α ≠ с, то β = с, отже, ВС – основа рівнобедреного трикутника, AB і АС – бічні сторони.

323. Оскільки даний трикутник рівнобедрений, то периметр Р = α + 2β, де α – основа, β – бічна сторона.

1) Якщо β = 6 см, то α = Р – 2β = 23 – 12 = 11 (CM).

2) Якщо α = 3 см, то Трикутник і його елементи

3) Якщо α = β + 2, то (β + 2) + 2β = 23; 3β = 21; β = 7 (см), а = 7 + 2 = 9 (см).

Відповідь: 1) 11 см; 2) 10 см; 3) 7 см, 7 см, 9 см.

324.

Трикутник і його елементи

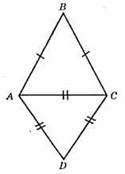
Нехай? АВС – рівнобедрений, ?ADC – рівносторонній.

Оскільки АС = CD = AD, то АС = 30/3 = 10 (см), тоді

Трикутник і його елементи

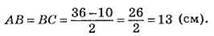
Відповідь: 10 см, 13 см, 13 см.

325. 1) Периметр трикутника не може дорівнювати 14 см, бо в такому разі третя сторона дорівнює 14 см – 4 см – 7 см = 3 см, а трикутника зі сторонами 4 см, 7 см, 3 см не існує, бо не виконується нерівність трикутника, оскільки 7 см = 4 см + 3 см.

2) Периметр трикутника може дорівнювати 21 см, оскільки третя сторона дорівнює 21 см – 7 см – 4 см = 10 см і виконується нерівність трикутника 10 см < 7 см + 4 см.

3) Периметр трикутника не може дорівнювати 31 см, бо в такому разі третя сторона дорівнює 31 см – 7 см – 4 см = 20 см, а трикутника зі сторонами 20 см, 7 см, 4 см не існує, бо не виконується нерівність трикутника, оскільки 20 см > 7 см + 4 см.

326. Якщо сторона трикутника дорівнює 36 мм, а периметр 70 мм, то сума двох інших сторін дорівнює 70 – 36 = 34 (мм). Тоді за нерівністю трикутника маємо 36 < 34. Оскільки отримана нерівність неправильна, то не існує трикутника зі стороною 36 мм і периметром 70 мм.

327. Нехай α = 10 см, β = 14 см, с = β + 2 = 14 + 2 = 16 (см). Тоді Р = α + β + с = 10 см + 14 см + 16 см = 40 см.

Відповідь: 40 см.

328. Нехай α = х см, тоді β = 2х см, с = 15 см. За умовою задачі маємо рівняння: х + 2х + 15 = 45; 3х = 30; х = 10. Отже, невідомі сторони трикутника 10 см і 20 см.

Відповідь: 10 см, 20 см.

329.

Трикутник і його елементи

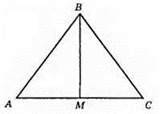
Р? ABC =АВ + ВС + АС = 15 см; Р? ABM = АВ + ВМ + AM = 11 см; P? BCM = ВС + СМ + ВМ = 14 см. Оскільки Р? ABM + P? BCM = Р? ABC + 2ВМ, то маємо: 11 см + 14 см = 15 см = 2ВМ; 2ВМ = 10 см; ВМ = 5 см.

Відповідь: 5 см.

330.

Трикутник і його елементи

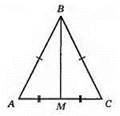
Нехай в рівнобедреному трикутнику ABC (AB = ВС), ВМ – медіана, AM = MC. Тоді Р? ABM = AB + ВМ + AM, враховуючи, що AB = ВС, AM = MC, маємо: AB + ВМ + AM = ВС + ВМ + MC = P? BCM. Отже, Р? ABM = P? BCM.

331.

Трикутник і його елементи

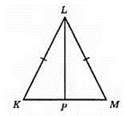
Нехай КМ = 10 см, KL = LM = 13 см. LP – медіана, Р? KLP = 30 см. Оскільки КР = 1/2КМ = 1/2 • 10 = 5 (см), Р? KLP = KL + LP + KP, 30 = 13 + LP + 5, звідси LP = 12 (см).

Відповідь: 12 см.

332. 1) Оскільки кути трикутника дорівнюють 1/6, 1/3, 1/2 частинам розгорнутого кута, то вони дорівнюють 1/6 • 180° = 30°, 1/3 • 180° = 60°, 1/2 • 180° = 90°. Отже, трикутник – прямокутний.

2) Оскільки кути трикутника дорівнюють 1/9, 1/3, 5/9 частинам розгорнутого кута, то вони дорівнюють 1/9 • 180° = 20°, 1/3 • 180° = 60°, 5/9 • 180° = 100°. Отже, трикутник – тупокутний.

3) Оскільки кути трикутника дорівнюють 1/3, 2/9, 4/9 частинам розгорнутого кута, то вони дорівнюють 1/3 • 180° = 60°, 2/9 • 180° = 40°, 4/9 • 180° = 80°. Отже, трикутник – гострокутний.

333. 1) Якщо бісектриса трикутника утворює зі стороною кута кут, що дорівнює 25 % розгорнутого кута, то градусна міра цього кута дорівнює 180° х 0,25 = 45°, а кут трикутника дорівнює 2 х 45° = 90°. Отже, трикутник – прямокутний.

2) Якщо бісектриса трикутника утворює зі стороною кута кут, що дорівнює 50 % прямого кута, то градусна міра цього кута дорівнює 90° х 0,5 = 45°, а кут трикутника дорівнює 2 х 45° = 90°. Отже, трикутник – прямокутний.

3) 1) Якщо бісектриса трикутника утворює зі стороною кута кут, що дорівнює 30 % розгорнутого кута, то градусна міра цього кута дорівнює 180° х 0,3 = 54°, а кут трикутника дорівнює 2 х 54° = 108°. Отже, трикутник – тупокутний,

4) Якщо бісектриса трикутника утворює зі стороною кута кут, що дорівнює 60 % прямого кута, то градусна міра цього кута дорівнює 90° х 0,6 = 54°, а кут трикутника дорівнює 2 х 54° = 108°. Отже, трикутник – тупокутний.

334. 1) Так.

Трикутник і його елементи

2)

Трикутник і його елементи

3) Ні. Трикутник буде прямокутний.

Трикутник і його елементи

335. 1) Третьою стороною не може бути сторона, що дорівнює 5 см, оскільки тоді не буде виконуватись нерівність трикутника, бо 12 см > 5 см + 5 см. Третьою стороною може бути сторона, що дорівнює 12 см, оскільки виконується нерівність трикутника, бо 12 см< 12 см + 5 см. Отже, третя сторона – 12 см.

2) Третьою стороною не може бути сторона, що дорівнює 6 см, оскільки тоді не буде виконуватись нерівність трикутника, бо 15 см > 6 см + 6 см. Третьою стороною може бути сторона, що дорівнює 15 см, оскільки виконується нерівність трикутника, бо 15 см < 15 см + 6 см. Отже, третя сторона – 15 см.

3) Третьою стороною не може бути сторона, що дорівнює 7 см, оскільки тоді не буде виконуватись нерівність трикутника, бо 14 см > 7 см + 7 см. Третьою стороною може бути сторона, що дорівнює 14 см, оскільки виконується нерівність трикутника, бо 14 см < 14 см + 7 см. Отже, третя сторона – 14 см.

Відповідь: 1) 12 см; 2) 15 см; 3) 14 см.

336. Нехай α – основа рівнобедреного трикутника, тоді бічна сторона – β = αn, периметр P = α + 2β = α + 2αn. Звідси 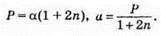Трикутник і його елементи

1) Якщо n = 2, Р = 50 см, то 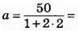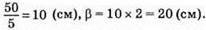Трикутник і його елементиТрикутник і його елементи Отже, сторони трикутника дорівнюють 10 см, 20 см, 20 см.

2) Якщо n = 3, Р = 35 см, то 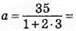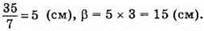Трикутник і його елементиТрикутник і його елементи Отже, сторони трикутника дорівнюють 5 см, 15 см, 15 см.

3) Якщо n = 4, Р = 63 см, то 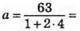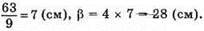Трикутник і його елементиТрикутник і його елементи Отже, сторони трикутника дорівнюють 7 см, 28 см, 28 см.

Відповідь: 1)10 см, 20 см, 20 см; 2) 5 см, 15 см, 15 см; 3) 7 см, 28 см, 28 см.

337. Друга сторона трикутника дорівнює 7 x 2 = 14 (см), третя сторона дорівнює 14 – 4 = 10 (см). Отже, периметр трикутника дорівнює 7 см + 14 см + 10 см = 31 см.

Відповідь: 31 см.

338. Нехай α, β і с – сторони трикутника, тоді α + β = 20 см, β + с = 22 см, α + с = 28 см. Додамо почленно три останні рівності α + β + β + c + α + c = 20 + 22 + 28; 2(α + β + с) = 70; α + β+ c = 70 : 2 = 35 (см).

Відповідь: 35 см.

339. CM – медіана, Р? ACM = P? CMB. Оскільки Р? ACM =АС + СМ + АМ, P? CMB = ВС + CM + MB і ці периметри рівні, то АС + CM +АМ – ВС + CM + MB. Враховуючи, що АМ = МВ, маємо АС = ВС. Отже, ?ABC – рівнобедрений.

Трикутник і його елементи

340. 1)

Трикутник і його елементи

2)

Трикутник і його елементи

341.

Трикутник і його елементи

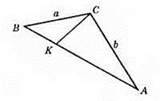
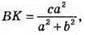
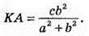
Основа висоти ділить гіпотенузу AB на відрізки, що відносяться як α2 : β2, починаючи від вершини В, отже, ці відрізки відповідно дорівнюють Трикутник і його елементи Трикутник і його елементи

1) Якщо α = 6 см, β = 8 см, с = 10 см, тоді

Трикутник і його елементи

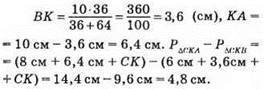
2) Якщо α = 7 см, β = 24 см, с = 25 см, тоді

Трикутник і його елементи

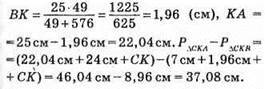
3) Якщо α = 5 см, β = 12 см, с = 13 см, тоді

Трикутник і його елементи

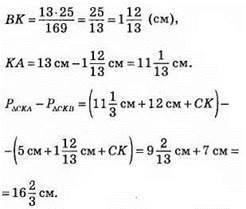
Відповідь: 1) 4,8 см; 2) 37,08 см; 3) 16 • 2/3 см.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. ТРИКУТНИК І ЙОГО ЕЛЕМЕНТИ Основна ідея, якою пройнята вся математика, – це ідея рівності. Г. Спенсер РОЗДІЛ 3 ТРИКУТНИКИ У цьому розділі ви повторите свої знання про трикутники, здобуті в попередніх класах, і дізнаєтеся про багато інших їх властивостей. Основне в розділі – три ознаки рівності трикутників Вони часто використовуються в геометрії. Тому від того, як добре ви вивчите […]...

  2. Трикутник та його елементи Урок № 15 Тема. Трикутник та його елементи Мета: домогтися засвоєння учнями змісту понять: “трикутник”; “сторона, вершина, кут (внутрішній) трикутника”; “кут, протилежний стороні”; “кут, прилеглий до сторони”; “периметр трикутника”; “внутрішня та зовнішня область трикутника”. Сформувати вміння: – розпізнавати та називати елементи трикутників, зображених на рисунку; – за рисунком та символічним позначенням трикутника називати кути, протилежні […]...

  3. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  4. Трикутник і його види Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 14. Трикутник і його види З усіх многокутників трикутники мають найменшу кількість сторін. Трикутники можна розрізняти за видом їх кутів. Якщо всі кути трикутника гострі, то його називають гострокутним трикутником (рис. 117). Якщо один із кутів трикутника прямий, то його […]...

  5. Многокутник та його периметр. Трикутник. Види трикутників Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 21. Многокутник та його периметр. Трикутник. Види трикутників Якщо кінець ламаної збігається з її початком, то таку ламану називають замкненою. На малюнку 137 зображено замкнену ламану, що складається з п’яти ланок, причому ланки ламаної не перетинаються. Таку ламану називають многокутником. Зауважимо, що […]...

  6. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  7. ТРИКУТНИК ТА ЙОГО ВИДИ РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ § 10. ТРИКУТНИК ТА ЙОГО ВИДИ Ви знаєте, що трикутник – це окремий вид многокутника. У нього 3 вершини, 3 сторони і 3 кути. Трикутник ABC на малюнку 119 має вершини А, В і С, сторони АВ, ВС i АС, кути ВАС, ABC і АСВ. Серед трикутників […]...

  8. Рівняння. Кути. Прямокутник. Трикутник і його види УРОК 41 Тема. Рівняння. Кути. Прямокутник. Трикутник і його види Мета: підготовити учнів до тематичної контрольної роботи. Тип уроку: повторення і систематизація знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Знайти корінь рівняння: 1) х + 15 = 29; 2) 30 – х = 17; 3) х – 12 = 19; 4) 12 […]...

  9. РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...

  10. Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...

  11. Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...

  12. Трикутник і його види Урок 40 Тема. Трикутник і його види Мета: подальше закріплення знань учнями класифікації трикутників, доповнення їх алгоритмами побудови трикутників за двома сторонами і кутом між ними та за стороною і прилеглими кутами; формування вмінь розв’язування задач на побудову і вдосконалення вмінь розв’язувати задачі на обчислення периметрів прямокутника, квадрата і трикутника. Тип уроку: застосування знань, умінь, […]...

  13. Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...

  14. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  15. КОЛО І ТРИКУТНИК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 20. КОЛО І ТРИКУТНИК Коло і трикутник можуть не мати спільних точок або мати 1, 2, 3, 4, 5, 6 спільних точок (відповідні малюнки виконайте самостійно). Заслуговують на увагу випадки, коли коло проходить через усі три вершини трикутника або коли воно дотикається до всіх сторін трикутника. Розглянемо […]...

  16. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  17. Трикутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Трикутник На рисунку зображений трикутник зі сто­ронами a, b і c. – формула периметра трикутника. Сума всіх кутів довіль­ного трикутника до­рів­нює . Кожний трикутник має принаймні два ­гострих кути. Види трикутників Види трикутників залежно від величини кутів (див. рисунок): а – гострокутний (усі кути гострі); б – тупокутний […]...

  18. ПРЯМОКУТНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 16. ПРЯМОКУТНИЙ ТРИКУТНИК Трикутник наливають прямокутним, якщо один із його кутів – прямий. Сума двох інших його кутів дорівнює 90°, бо 180° – 90° = 90°. Сторона прямокутного трикутника, що лежить проти прямого кута, – це гіпотенуза, дві інші його сторони – катети (мал. 196). На малюнку прямий кут іноді позначають […]...

  19. Рівнобедрений трикутник Урок № 23 Тема. Рівнобедрений трикутник Мета: домогтися свідомого розуміння учнями понять: – умова та висновок теореми; – пряма та обернена теореми; – формулювання та доведення ознаки рівнобедреного трикутника. Сформувати вміння: – відтворювати теорему – ознаку рівнобедреного трикутника; – виділяти у формулюванні теореми умову та висновки; – використовуючи знання про пряму та обернену теореми, складати […]...

  20. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  21. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  22. Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...

  23. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  24. Коло, вписане в трикутник Урок № 50 Тема. Коло, вписане в трикутник Мета: домогтися засвоєння учнями змісту поняття кола, що вписане в трикутник, теореми про це коло, схеми її доведення та наслідку з неї. Сформувати вміння: – відтворювати формулювання означення і теореми про вписане в трикутник коло; – за описом об’єктів розрізняти ті, в яких мова йде про коло, […]...

  25. ТРИКУТНИК. СТОРОНА, ВЕРШИНА, КУТ ТРИКУТНИКА. ПОРІВНЯННЯ ПРЕДМЕТІВ (“НАЙДОВШИЙ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 12. ТРИКУТНИК. СТОРОНА, ВЕРШИНА, КУТ ТРИКУТНИКА. ПОРІВНЯННЯ ПРЕДМЕТІВ (“НАЙДОВШИЙ – НАЙКОРОТШИЙ”, “ОДНАКОВІ ЗА ДОВЖИНОЮ”) Мета: ознайомити учнів із трикутником, його елементами; вчити порівнювати предмети (“найдовший – найкоротший”, “однакові за довжиною”); розвивати мислення; виховувати старанність. Хід уроку І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПОВТОРЕННЯ […]...

  26. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  27. Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...

  28. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  29. НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...

  30. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  31. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  32. Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектри­си) рівні між собою....

  33. Рівносторонній трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Рівносторонній трикутник Усі висоти, медіани й бісектриси мають однакову довжину. Вписане і описане коло мають спільний центр. Середня лінія трикутника – відрізок, що сполучає середини двох сторін трикутника. Теорема: Зовнішній кут трикутника – кут, суміжний із внутрішнім кутом трикутника. Теорема: Теорема косинусів: у будь-якому трикутнику зі сторонами а, b, с […]...

  34. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  35. Теорема синусів Геометрія Розв’язування трикутників Теорема синусів Теорема 1 (синусів). Сторони трикутника пропорційні до синусів протилежних кутів. У трикутнику, зображеному на рисунку, за теоремою синусів маємо: . Теорема 2. Якщо R – радіус кола, описаного навколо трикутника, то , або , де a – сторона трикутника, а – протилежний цій стороні кут. Теорема 3. У трикутнику проти […]...

  36. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  37. Многокутники. Розв’язування задач Урок № 49 Тема: Многокутники. Розв’язування задач Мета. Формувати в учнів уміння і навички самостійно застосовувати вивчений матеріал, до розв’язування задач, розвивати навички самостійної пізнавальної роботи, розвивати вміння самостійної роботи, розвивати вміння аналізувати, робити висновки. Форми роботи: математичний диктант, бесіда, розв’язування задач і виконання вправ. Обладнання: лінійка, кольорова крейда, косинець. Тип уроку: урок узагальнення і […]...

  38. Знаходження площі трикутника за двома сторонами і кутом між ними УРОК № 12 Тема. Знаходження площі трикутника за двома сторонами і кутом між ними Мета уроку: виведення формули для знаходження площі трикутника за двома сторонами і кутом між ними. Формування вмінь застосовувати виведену формулу до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: […]...

  39. Ознаки паралельності прямих. Сума кутів трикутника Урок № 40 Тема. Ознаки паралельності прямих. Сума кутів трикутника Мета: перевірити рівень засвоєння знань та вмінь, передбачених програмою, із зазначених тем. Тип уроку: контроль та корекція знань. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою. Роботу оцінити та врахувати в тематичному балі. III. Умова контрольної роботи […]...

  40. Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...

Ви зараз читаєте: Трикутник і його елементи
«
»