ТРИКУТНИК ТА ЙОГО ВИДИ
РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ
§ 10. ТРИКУТНИК ТА ЙОГО ВИДИ
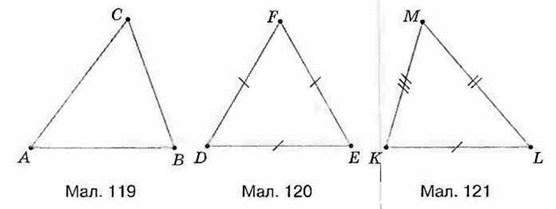
Ви знаєте, що трикутник – це окремий вид многокутника. У нього 3 вершини, 3 сторони і 3 кути. Трикутник ABC на малюнку 119 має вершини А, В і С, сторони АВ, ВС i АС, кути ВАС, ABC і АСВ.
Серед трикутників можна виділити кілька видів. Для цього треба обрати основу поділу трикутників на види. Найперше спадає на думку – порівняти довжини сторін трикутника.
Сторони трикутника можуть мати ту саму довжину. Тоді трикутник, як і будь-який многокутник із такою властивістю,
На малюнку рівні сторони трикутника позначають однаковою кількістю рисочок.
У трикутника може не бути рівних сторін, як, наприклад, у трикутника KLM на малюнку 121. Тоді такий трикутник називають різностороннім.
Якщо ж у трикутника є дві рівні сторони, то його називають рівнобедреним. На малюнку 122 ви бачите рівнобедрений трикутник RST, у якогоRT = ST. Рівні сторони рівнобедреного трикутника називають його бічними сторонами, а третю сторону – основою.
Ви вже знаєте, що таке периметр многокутника
Р = 3а.
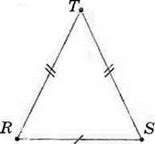
Мал. 122
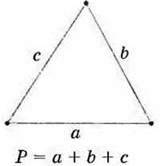
Мал. 123
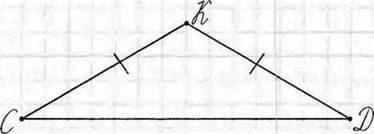
Задача. Знайдіть периметр рівнoбедреного трикутника CDK, у якого основа CD=5 см, а бічна cторона – на 2 см менша.
Розв’язання.
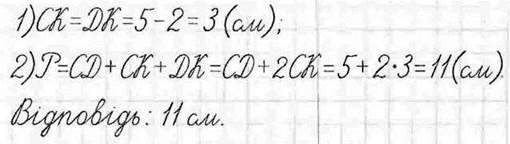
? Чи можна поділити трикутники на види за іншою основою? Так. Наприклад, за їх кутами.
Серед трикутників розрізняють гострокутні, прямокутні й тупокутні трикутники.
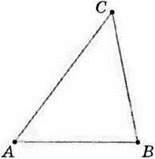
У гострокутного трикутника всі кути є гострими. Наприклад, на малюнку 124 ви бачите гострокутний трикутник ABC.
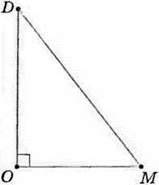
У прямокутного трикутника один кут є прямим. Наприклад, у трикутника DOM (мал. 125) кут
0 дорівнює 90°.
На малюнку прямий кут трикутника позначають знаком “┘”.
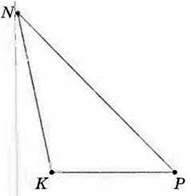
У тупокутного трикутника один кут є тупим. Наприклад, у трикутника KPN на малюнку 126 ∠ NKP > 90°.
? Чи існує трикутник із двома прямими чи двома тупими кутами? Ні.
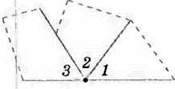
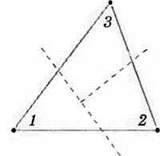
Проведемо дослід. Виготовимо трикутник із цупкого паперу розріжемо його так, як показано на малюнку 127. До кута 1 прикладемо кут 2 (мал. 128),
Мал. 124
Мал. 125
Мал. 126
Мал. 127
Мал. 128
А до нього – кут 3. Дістали розгорнутий кут. Це означає, що сума кутів 1, 2 і 3 дорівнює 180°. Таку властивість має будь-який трикутник. Звідси випливає, що в трикутнику не може бути два тупих чи два прямих кути. У 7 класі ви зможете це строго довести.
Сума кутів трикутника завжди дорівнює 180°, а периметр трикутника залежить від довжин його сторін.
Мал. 129
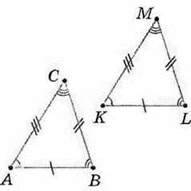
Ви знаєте, що таке рівні многокутники. Аналогічно, два трикутники називаються рівними, якщо вони суміщаються накладанням. Звідси випливає, що у рівних трикутників рівні відповідні сторони і відповідні кути. На малюнку 129 ви бачите рівні трикутники ABC і KLM. У них:
АВ = KL, ВС = LM, АС = КМ,
∠A=∠K, ∠B=∠L, ∠C = ∠M.
Щоб з’ясувати, чи рівні два трикутники, треба перевірити, чи виконуються всі ці шість рівностей. У 7-му класі ви дізнаєтесь, як можна спростити цю процедуру.
Дізнайтеся більше
Наведемо найбільш важливі випадки, які зустрічаються під час побудови трикутників. З іншими випадками ви познайомитесь пізніше, вивчаючи курс геометрії.
Якщо дано дві сторони і кут між ними, то трикутник можна побудувати завжди.
Якщо дано сторону і два кути, то трикутник можна побудувати лише за умови, що сума двох даних кутів менша від 180°. Якщо дано три сторони, то трикутник можна побудувати лише за умови, що кожна з його сторін менша від суми двох інших сторін.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
249. Назвіть вершини, сторони, кути трикутника:
1) ABC; 2) MNP; 3) DRT.
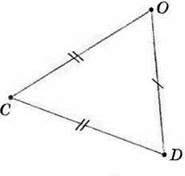
350. На малюнках 130-132 назвіть:
1) рівносторонній трикутник; 2) рівнобедрений трикутник.
Мал. 130
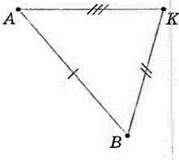
Мал. 131
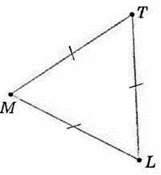
Мал. 132
351. Назвіть основу та бічні сторони рівнобедреного трикутника: 1) ABC (мал. 133); 2) MNP (мал. 134).
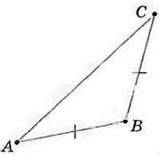
Мал. 133
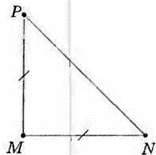
Мал.134
Мал. 134
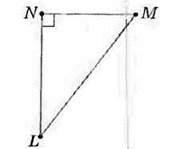
Мал. 135
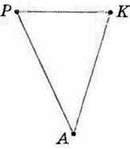
Мал. 136
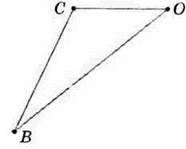
Мал. 137
352.Назвіть вид трикутника ABC, якщо:
1) АВ = 3 см, ВС = 8 см, СА= 8 см;
2) АВ = 15 м, ВС = 15 м, СА – 15 м.
353. Знайдіть периметр рівностороннього трикутника зі стороною: 1) 15 см; 2) 123 м.
354. На малюнках 135-137 назвіть:
1) гострокутний трикутник; 2) тупокутний трикутник; 3) прямокутний трикутник.
355. Назвіть вид трикутника ABC, якщо:
1) ∠A = 90°, ∠В = 20°, ∠С = 70°;
2) ∠A = 45°, ∠B =65°, ∠C = 70°;
3) ∠A = 14°, ∠ В = 126°, ∠C = 40°.
356. Чи може сума всіх кутів трикутника дорівнювати:
1)100°; 2)170°; 3)180°; 4)190°?
357. Побудуйте трикутник. Виміряйте його сторони та визначте його вид.
356. Побудуйте: 1) рівнобедрений трикутник; 2) різносторонній трикутник. Проведіть необхідні вимірювання та знайдіть периметр кожного трикутника.
359. Дано трикутник ABC. Знайдіть невідомі величини за таблицею 11.
Таблиця 11
АВ | 18 см | 67 м | 125 см | 945 дм | 556 см |
АС | 34 см | 20 м | 65 дм | ||
ВС | 23 см | 23 м | 125 см | 876 дм | 4500 мм |
P | 144 м | 375 см |
360. Обчисліть периметр рівностороннього трикутника ABC, якщо:
1) АВ = 201 см; 3) АВ= 37 см;
2) АС = 4 м 6 см; 4) СВ = 8 м 30 см.
361. Знайдіть сторону рівностороннього трикутника, якщо його периметр дорівнює: 1) 27m 2) 15р; 3) 6а.
362. Основа рівнобедреного трикутника дорівнює 10 мм, а бічна сторона – вдвічі більша за неї. Знайдіть периметр трикутника.
363. Бічна сторона рівнобедреного трикутника дорівнює 18 см, а його периметр – 42 см. Знайдіть основу трикутника.
364. Побудуйте трикутник: 1) гострокутний; 2) тупокутний;
3) прямокутний.
365. Чи існує трикутник, у якого кути дорівнюють:
1) 90°, 90°, 20°; 3) 70°, 80°, 80°;
2) 135°, 90°, 45°; 4) 30°, 70°, 80°?
366. Дано трикутник ABC. За даними таблиці 12 знайдіть невідомі кути.
Таблиця 12
∠А | 60° | 60° | 60° | 135° |
∠В | 30° | 42° | 90° | 20° |
∠С | 100° | 45° |
367. Кут А трикутника ABC дорівнює 40°, а кут С – удвічі більший за кут А. Знайдіть кут B.
368. Кут А трикутника ABC дорівнює 70°, а кут С – на 10° більший за кут А. Знайдіть кут В.
369. За допомогою лінійки і транспортирна побудуйте трикутник ABC, у якого:
1) ∠ А = 60°, ∠В = 6 см, АС = 4 см;
2) ∠ А = 60°, ∠В = 90°, АВ = 5 см.
З’ясуйте вид трикутника.
370. За допомогою лінійки і транспортира побудуйте трикутник ABC, у якого:
1) ∠A = 60°, ∠В = 60°, АВ = 6 см;
2) ∠A = 60°, ∠В = 6 см, АС = 6 см.
З’ясуйте вид трикутника.
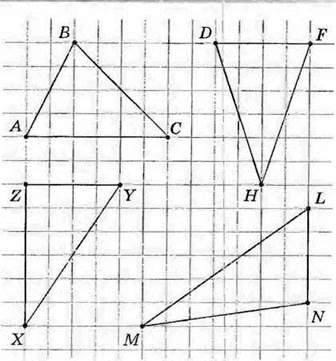
Мал. 138
371. На малюнку 138 зображено трикутники. У зошиті побудуйте трикутники, рівні даним.
372. Сторона АВ трикутника ABC дорівнює 10 см. Сторона АС удвічі більша за АВ і на 6 см менша, ніж ВС. Знайдіть периметр трикутника.
373. Сторона ВС трикутника ABC дорівнює 17 см. Сторона АС на 8 см більша за ВС і на 6 см менша від АВ. Знайдіть периметр трикутника.
374. Основа рівнобедреного трикутника на 10 см більша за бічну сторону. Знайдіть периметр трикутника, якщо його бічна сторона дорівнює 4 дм.
375. Бічна сторона рівнобедреного трикутника на 9 см більша за основу. Знайдіть периметр трикутника, якщо його основа дорівнює 56 см.
376. Чому дорівнює сторона рівностороннього трикутника, периметр якого вдвічі менший за пери, метр квадрата зі стороною 12 см?
377. Кут С трикутника ABC дорівнює 60°. Кут В – на 40° менший від кута А, Знайдіть кут В.
378. У трикутнику ABC ∠ В – прямий ∠ А на 56° більший за LC. Знайдіть кути трикутника.
379. Побудуйте:
1) рівнобедрений гострокутний трикутник;
2) рівнобедрений тупокутний трикутник;
3) рівнобедрений прямокутний трикутник.
380. Сторона АВ трикутника ABC на 7 см більша за сторону АС, яка на 6 см менша від сторони ВС. Знайдіть сторони трикутника, якщо його периметр дорівнює 49 см.
381. У трикутнику ABC АВ + ВС = 25 см, ВС + СА = 26 см, СА+АВ = 27 см. Знайдіть периметр трикутника ABC і кожну його сторону.
382. Периметр рівнобедреного трикутника дорівнює р см, а його бічна сторона – (m + 3) см. Знайдіть основу трикутника.
383. У трикутнику ABC ∠А + ∠B = 90°, ∠B + ∠C= 150°. Знайдіть кути трикутника.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
384. Папір має форму прямокутника, одна сторона якого дорівнює 4 см, а друга – 9 см. Розріжте прямокутник на дві рівні частини так, щоб можна було, склавши їх, отримати трикутник.
385. На уроці трудового навчання Марійка отримала завдання пошити трикутну косинку розмірами 50 см, 50 см, 75 см. Дівчинка вирішила оздобити косинку мереживом. Скільки їй треба купити мережива, щоб обшити косинку?
386. Побудуйте орнамент, використовуючи: 1) різні види трикутників; 2) тільки прямокутні трикутники.
ЗАДАЧІ НА ПОВТОРЕННЯ
387. Обчисліть:
1) 25 ∙ 8 – 4 ∙ 90 + 2 ∙ (424 + 26);
2) 240:4 + 560:7+121 : (321 -240 – 70).
388. Запишіть у міліметрах:
1) 25 см 4 мм; 2)8м2мм.
389. Запишіть у секундах:
1) 2 год 15 хв; 2) 1 год 20 хв 5 с.
390. У зимових Олімпійських іграх у Ванкувері брали участь спортсмени з 83 країн, що на 123 країни менше, ніж у літній Олімпіаді в Пекіні. Скільки країн взяло участь у літніх іграх?
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Що називається буквеним виразом? Наведіть приклад.
2. Поясніть, як обчислити значення буквеного виразу.
3. Що таке формула? Наведіть приклад формули.
4. Назвіть компоненти і результат дії додавання.
5. Запишіть переставний закон додавання.
6. Поясніть, як додають багатоцифрові числа. Наведіть приклад.
7. Запишіть сполучний закон додавання. Наведіть приклад його застосування,
8. Назвіть компоненти і результат дії віднімання.
9. Що означає відняти від одного числа друге?
10. Поясніть, як віднімають багатоцифрові числа. Наведіть приклад.
11. Що називається многокутником?
12. Який многокутник називається прямокутником? Квадратом?
13. Які фігури називаються рівними?
14. Що називається периметром многокутника?
15. Запишіть формулу периметра n-кутника, кожна сторона якого дорівнює а.
16. Як знайти периметр квадрата? Прямокутника?
17. Який многокутник називається трикутником?
18. Який трикутник називається рівностороннім? Різностороннім? Рівнобедреним?
19. Який трикутник називається гострокутним? Прямокутним? Тупокутним?
20. Як знайти периметр трикутника?
21. Запишіть формулу периметра Рівностороннього трикутника.
22. Чому дорівнює сума кутів трикутника?
ТЕСТОВІ ЗАВДАННЯ.
Уважно прочитайте задачі і знайдіть серед запропонованих відповідей правильну. Для виконання тестового і завдання потрібно 10-15 хв.
1. Знайдіть суму чисел 114 і 938.
A. 1142.
Б. 1042.
B. 1052.
Г. 1152.
2. Число а збільшили на 15, потім збільшили в 3 рази, а потім зменшили на 15. Який вираз отримали?
A. За.
Б. а + 15 ∙ 3-15.
B. (а + 15) ∙ (3 – 15).
Г. (а+15) -3- 15.
3. У трикутнику ABC ∠ А = 80°, ∠ В = 20°, ∠ С = 80°. Якого виду трикутник ABC?
A. Рівносторонній.
Б. Прямокутний.
B. Гострокутний.
Г. Тупокутний.
4. Бічна сторона рівнобедреного трикутника дорівнює 9 см, а його основа – на 5 см більша. Знайдіть периметр трикутника.
A. 23 см.
Б. 37 см.
B. 32 см.
Г. 14 см.
6. Сторона АВ чотирикутника ABCD дорівнює стороні квадрата, периметр якого дорівнює 24 см. Сторона CD – на 4 см більша за АВ і на 3 см менша від СВ. Сторона AD – на 20 мм більша за суму сторін АВ і CD. Знайдіть периметр чотирикутника.
A. 49 см.
Б. 37 см.
B. 47 см.
Г. 41 см.