Усні обчислення на основі нумерації багатоцифрових чисел
Усні обчислення на основі нумерації багатоцифрових чисел
268. Обчисліть.
6789 – 700 6789 – 80 6 789 – 9 6789 – 789
73 859 + 1 86 749 – 1 70 000 + 500 + 30 + 9
8 429 – 8 000 6 419 – 400 6 379 – 70 3 759 – 9
269. Проведіть на аркуші паперу два промені ВА і ВС зі спільним початком у точці В. Розгляньте фігуру, яку ви накреслили.
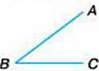
– Розгляньте малюнки, що подані внизу. Про що ви з них дізналися?
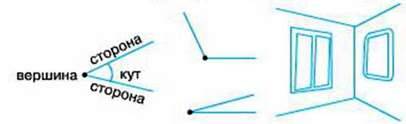
Порівняйте свій висновок із поданим поясненням.
Фігуру, утворену двома променями, які виходять
Точка В, із якої проводили промені, називається вершиною кута. А промені ВА і ВС – це сторони кута. Кути можна побачити скрізь, наприклад, у будь-якій кімнаті.
Кут – геометрична фігура, утворена двома променями (сторонами кута), які виходять із однієї точки, що називається вершиною кута. Кут позначають однією великою або трьома великими буквами латинського алфавіту. Для позначення кута замість слова “кут” використовують позначку “∠”, наприклад: ∠ASC.
270. Для заготівок на зиму мама купила на базарі 12 кг огірків по 8 грн і 15 кг помідорів по 6 грн. Скільки грошей витратила
– Що означають вирази: 12 ∙ 8; 15 ∙ 6; 15 + 12; 8 + 6; 15 – 12; 8 – 6?
– Накресліть таблицю до умови задачі.
– Розв’яжіть задачу, склавши вираз до неї.
Сергій склав схеми розв’язків до задачі.
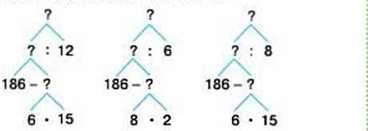
– Подумайте, чи можуть це бути обернені схеми до попередньої задачі. Якщо так, тоді складіть і розв’яжіть свою задачу до однієї з поданих схем.
271. Розв’яжіть рівняння.
10 000 – х = 9 998.
Виконайте вдома
272. Виконайте зазначені дії:
1. зменшіть найбільше п’ятицифрове число на 9; 90; 900;
2. зменшіть найменше п’ятицифрове число на 1; 10; 100; 1000.
273. Присадибна ділянка має форму прямокутника. Довжина садиби – 70 м, а ширина 42 м.  Площі садиби займають будівлі, двір і сад, а решту площі – город. Яку площу займає город?
Площі садиби займають будівлі, двір і сад, а решту площі – город. Яку площу займає город?
274. Виконайте обчислення за поданим зразком.
56 000 + 32 000 = 56 тис. + 32 тис. = 88 тис. = 88 000
7 000 – 49 000
52 000 + 16 000
275. Обчисліть вирази.
300 : 10 : 10
500: 100 ∙ 566 – 6 ∙ 9 + 1
120 – 20 + 4 ∙ 5
– За допомогою дужок змініть порядок дій і знайдіть значення виразів.
276. У трьох класах навчається 94 учні. Скільки учнів у кожному класі, якщо відомо, що у другому класі на 8 учнів більше, ніж у першому класі, а в третьому класі на 6 учнів більше, ніж у другому класі?
– Оберіть відповідну схему до задачі.
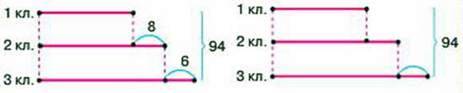
– Чи можна загальну кількість дітей, які навчаються в трьох класах, розділити на кількість класів?
Віка запропонувала скористатися способом урівнювання відрізків: обравши найкоротший відрізок, треба всі відрізки прирівняти до його довжини. Тоді число 94 зменшиться на суму чисел: 8 + 8 + 6.
Роман, продовжуючи міркування Віки, записав такий вираз: (94 + 8 + 6 + 6): 3. Чи можете ви погодитися з думкою хлопчика? Чому?
– Внесіть числа в дані схеми, яку ви обрали, і розв’яжіть задачу.
277. Поставте на сторінці зошита точку О. Проведіть від неї в рамі сторони промені так, щоб утворилась пряма лінія Розгляньте фігуру, що у вас вийшла. Зробіть висновки. Порівняйте свої міркування з поданим нижче поясненням
Кут, промені якого утворюють пряму, називають розгорнутим
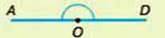
∠ AOD – розгорнутий
– Проведіть вертикальну лінію до точки О. Чи правильне твердження, що утворилися два рівні кути? Порівняйте свої міркування з поданим нижче поясненням.

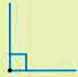
Кут, який становить половину розгорнутого кута, називається прямим.
Прямий кут можна побудувати за допомогою косинця. Кути сторінки книги, яку ми тримаємо в руках, – прямі, кути сторінок зошита – також прямі, кути письмового стола чи парти – прямі.
– Розгляньте малюнки. Чи відрізняються подані кути від прямого? Як саме? Порівняйте свої міркування з поданим нижче поясненням.
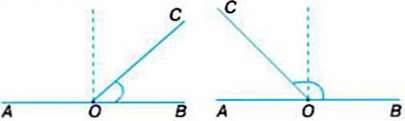
Кут, який менший за прямий, називається гострим.
Кут, який більший за прямий, але менший за розгорнутий, називається тупим.
Виконайте вдома
278. Першого дня літак пролетів 3000 км. другого – на 800 км більше, а третього дня пролетів на 500 км менше, ніж другого. Скільки кілометрів літак пролетів за 3 дні?
279. Чи можна порівняти числа, не відновлюючи цифри, замість яких стоять зірочки?
1. 63** і 61 **; 2. 28* і 1 **; 3. *1*і99*.
280. Чи можна, не обчислюючи, знайти значення виразів кожної пари нижнього рядка, використовуючи значення виразів верхнього рядка?
1.1000 + 1524; 5 431 – 4000; 10 000 – 9 700.
2.998 + 1524; 5 431 – 3996; 10 013 – 9 700.
Маша міркувала так:
998 + 1524 = 1000 + 1524 – 2 = 2522.
Катя записала такий вираз:
5431 – 3996 = 5431 – 4000 + 4 =1435.
Роман міркував так:
10 013 – 9 700 = 10 000 – 9 700 + 13 = 300 + 13 = 313.
– Поясніть, як міркували діти. Чи можна стверджувати, що вони використали спосіб округлення?
281. Обчисліть.
1300 + 499 1500 + 299 102 – 39 506 – 198
12 002 + 2999 10 309 + 498 401 – 19 506 – 297
282. У двох шафах зберігаються 154 книжки. Якщо з однієї шафи забрати 12 книжок, тоді в обох шафах книжок стане порівну. Скільки книжок стане у кожній шафі? Скільки книжок було в шафах спочатку?

– Розгляньте схеми до задач. Оберіть потрібну.
– Використайте спосіб урівнювання відрізків і розв’яжіть задачу.
– Подумайте, як іще можна урівняти число книг у шафах, не змінюючи їх загальної кількості. Накресліть схему. Запишіть розв’язок.
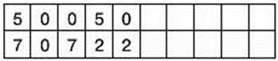
283. Як, маючи лише 2 посудини місткістю 5 л та 7 л, набрати з водопровідного крану 4 л води?
– Накресліть таблицю та виконайте такі дії:
1 крок – наповніть посудину місткістю 7 л;
2 крок – перелийте воду в посудину місткістю 5 л;
3 крок – вилийте з 5 л і т. д. – продовжте самостійно.
Виконайте вдома
284. До кіоска завезли 2520 примірників газет. До обіду продали 1340 примірників. На скільки більше примірників газет продали, ніж залишилось?
285. Накресліть кути: а) розгорнутий; б) прямий; в) гострий; г) тупий. Порівняйте їх. Запишіть за допомогою знаків “>”, “<“, “=”.
286. Діти обмислювали вирази. Розгляньте записи, які вони зробили, та поясніть їхні міркування.
Віка: 700 ∙ 7
7 сот. ∙ 7 = 49 сот.
700 ∙ 7 = (7 ∙ 100) ∙ 7 = 100 ∙ (7 ∙ 7) = 4900
700 ∙ 7 = 4900
Денне:
8 000 ∙ 4
8 тис. ∙ 4 = 32 сот.
8 000 ∙ 4 = 32 000
Сашко:
8 000 : 4
8 тис. : 4 = 2 тис.
8 000 : 4 = (8 ∙ 1000) : 4 = 8 : 4 ∙ 1000
8 000 : 4 = 2000
Максим:
64 000 : 4
64 тис. : 4 = 16 тис.
64 000 : 4 = 16000
287. За 3 хв автомат на молочному заводі закриває 3600 банок. Скільки таких банок автомат закриє за 9 хв?
288. У залі кінотеатру 510 місць. Коли школярі зайняли 8 повних рядів, у залі залишилось 270 вільних місць. Скільки всього рядів у залі кінотеатру, якщо всі ряди однакові?
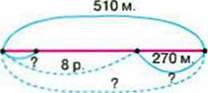
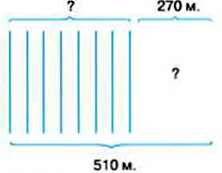
– Розгляньте схеми до задачі. Поясніть їх.
– Зробіть аналіз розв’язку задачі. Розв’яжіть її.
– Змініть запитання задачі так. щоб остання дія була дією віднімання.
289. Знайдіть значення виразу.
(21 000 – 3000) : 6 + 360 000 : З
– Перевірте дію віднімання додаванням.
290. Розгляньте малюнок. На площині розміщені у клітинках об’єкти. Запишіть їх розміщення.
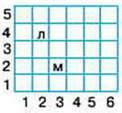
Катя записала так: лялька знаходиться в перетині четвертого ряду та другого стовпчика, а м’яч – у третьому ряду другого стовпчика.
Артем записав так: Л (2, 4); М (3, 2) і пояснив, що місце кожної клітинки записано за допомогою елементів, де перша цифра вказує на горизонтальне розташування, а друга – на вертикальне.
– Поміркуйте, чиє з пояснень дітей більш зручне.
291. Позначте в зошиті розміщення об’єктів на площині за їх елементами: Д (5, 4); К (4. 5).
Виконайте вдома
292. Накресліть прямокутник площею 35 см2. Поділіть його на квадрати. Покажіть, де розміщені об’єкти А (2, 4); В (3, 6).
293. Обчисліть.
4500 : 3 500 ∙ 4
4500 : 5 700 ∙ 8
2100 : 7 2400 ∙ 42
294. Розгляньте вирази у стовпчиках. Що означають вирази другого й третього рядків кожного стовпчика щодо виразів першого рядка?
84 : 12 48 : 12 42 : 14
84 : (6 ∙ 2) 48 : (6 ∙ 2) 42 : (7 ∙ 2)
84 = 12 ∙ 7 48 = 12 ∙ 4 42 = 14 ∙ 3
295. Діти розв’язували вираз: 6400 : 16.
Олена записала так:
6400 : (8 ∙ 2) = (6400 : 8): 2 = 800 : 2 = 400.
Сергій зробив такий запис:
64 сот. : 16 = 4 сот. = 400.
– Поясніть, як міркували діти.
296. Виконайте дії зручним для вас способом.
3600 : 12 72 000 : 24
4500 : 15 42 000 : 14
297. Часткою яких виразів можуть бути числа 9, 8, 7, 6? Запишіть ці вирази.
81 : 9 72 : 8 63 : 7 54 : 6 45 : 5 36 : 4
27 : 3 18 : 2 9 : 1 9 : 9 0 : 10
298. Сім’я фермера засолювала на зиму огірки. У перший день у 4 діжках засолили 24 кг огірків. У другий день огірків засолили на 12 кг більше, ніж у перший день. На скільки більше діжок огірків засолила сім’я в другий день?
– Учні накресли схеми до задачі та розв’язали їх. Микита записав 4 дії, а Наталка – лише 2 дії. Визначте, де чия схема. Поясніть, як міркували діти. Хто з дітей правильно розв’язав задачу?
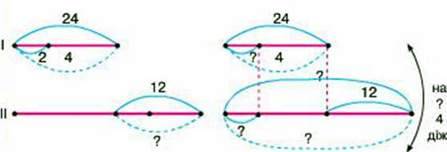
– Запишіть розв’язок до кожної задачі по діях.
Виконайте вдома
299. Обчисліть.
(285+ 15) : 3 ∙ 5 + 280 5 100 : 17 4800 : 12
400 – (60 + 30) : 10 ∙ 1 6 800 : 17 8 700 : 29
300. Накресліть прямокутник. Покажіть розміщення об’єкта за його елементами.
А (3, 6); В (4, 3); Д (2, 4); К (2, 3).
301. Розгляньте таблицю. Знайдіть значення зі змінною в.
В | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
840 : в |
302. Поясніть, як виконували дію ділення.
1. 3600 : 40 = 3600 : (10 ∙ 4) = 3600 : 10 : 4 = 90
Або: 360 дес.: 4 дес. = 90
2. 72 000 : 900 = 72 000 : (100 ∙ 9) = 72 000 : 100 : 9 = 80
Або: 720 сот. : 9 сот. = 80
303. Виконайте обчислення зручним для вас способом.
30 000 : 300 960 000 : 800 12 000 : 800
72 000 : 900 18 000 : 600 150 000 : 300
8 000 : 4000 9 000 : 300 24 000 : 600
304. Рон Уїзлі та Гаррі Поттер протягом дня разом прочитали стільки сторінок, скільки й Герміона. Рон прочитав 50 сторінок, що на 120 сторінок менше, ніж Гаррі. Скільки сторінок прочитав кожен із хлопчаків протягом тижня?
– Накресліть схему до умови задачі та розв’яжіть її.
– Що означає вираз: 120 ∙ 7?

305. Галині та Олені разом 26 років, а три роки тому Олена була старша від Галини в 4 рази. Скільки років Олені тепер?

– Розгляньте схеми. Обчисліть, скільки разом було років Галині й Олені 3 роки тому.
– Розв’яжіть задачу.
306. Розв’яжіть рівняння.
45 000 : х = 15 24 000 : х = 2
307. На площині розміщені об’єкти: А (5, 3); Д (2, 4); К (3, 5).
– Розгляньте малюнки. Який спосіб правильний? Яким способом якнайшвидше можна встановити місце розташування об’єктів? Який спосіб зручніший?
1 варіант
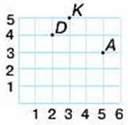
2 варіант
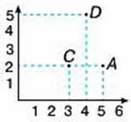
– Виконайте завдання другим способом. А (5, 2); Д (4,5); С (3, 2).
Виконайте вдома
308. У альбомі 100 аркушів. Скільки таких альбомів вийде із 15 000 аркушів? Скільки аркушів у 1000 таких альбомів?
309. Порівняйте числа.

310. Із чисел 2, 6, 0, 18 виберіть такі значення букви b, для яких буде правильною нерівність: 180 : b < 50.
311. У 14 бочок і 17 однакових банок розлили 503 л олії. У бочки наливали по 25 л олії. Скільки олії налили в банку?
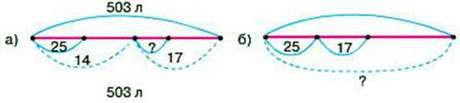
– Оберіть правильну схему. Розв’яжіть задачу.
312. Якими можуть бути сторони прямокутника, якщо його периметр 22 дм; 48 см; 40 мм?
313. Виконайте дії.
1. (1800 : 2 : 30 + 18) : 6 + (70 ∙ 7 – 140 : 2) : 60;
2. (60 – 16 : 4) : 8 ∙ 40 – (80 ∙ 8 – 20 ∙ 5): 6.
Виконайте вдома
314. Обчисліть.
340 + 80 ∙ 3 580 – 30 ∙ 4 7500 : 15
(260 + 380) : 4 (402 – 20) : 2 6400 : 16
315. Із чисел 2. 4, 10, 16 виберіть такі значення букви а, для яких буде правильною нерівність: 160 : а < 40.
316. Розгляньте, як учні виконували дію додавання.
– Катя знайшла суму чисел. Який закон вона використала?
237 + 190 = 190 + 237
А + b = b + а
– Який закон додавання використав Ілля?
(467 + 280) + 20 = 467 + (280 + 20)
(а + b) + с = а + (b + с)
– Ліза обчислила свій вираз так:
123 + 44 + 77 = (123 + 77) + 44 = 200 + 44 = 244.
– Чи можна стверджувати, що Ліза:
А) використала одночасно і переставний, і сполучний закони додавання;
Б) обрала зручний спосіб обчислення.
317. На скільки потрібно збільшити число 507 654, щоб змінилися цифри у розряді одиниць та десятків, а цифри в других розрядах залишилися без змін?

– На скільки збільшили число 507 654 у 1 варіанті та в 2 варіанті? Зробіть висновки. Чи можна дати інші варіанти відповіді на запитання?
318. Знайдіть значення суми.
4602 + 395 436
Денис записав так:

Маша записала так:

– Хто з дітей виконав задания правильно?
При додаванні багатоцифрових чисел користуйтеся способом порозрядного додавання, наприклад:

319. Виконайте обчислення в стовпчик. Визначте, скільки переходів через розряд треба виконати (покажіть стрілками).
38 204 + 41 893 453 278 + 43 721
352 406 + 46 292 507 843 + 9 235
320. Блокнот, підставка під книги й ручка коштують разом 90 грн. Блокнот і підставка під книги разом коштують 55 грн, а підставка під книги та ручка – 45 грн. Скільки коштує кожна річ окремо?
– Розгляньте схеми. Поясніть, як міркували, коли їх складали.
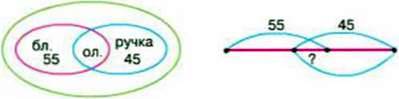
– Вартість якого предмета врахували 2 рази?
– Що означає вираз: 55 + 45?
321. Обчисліть.
260 529 + 392 271; 101 704 + 250 296.
322. За 3 дні зібрали 900 кг моркви. Першого дня зібрали третину всієї моркви, другого дня зібрали 110 кг моркви, а третього дня зібрали решту. Скільки кілограмів моркви зібрали третього дня?
323. Розгляньте, як учні Роман і Віка виконували дію додавання.
– Яким законом віднімання користувався Роман?
1. (247 + 159) – 147 = (247 – 147) + 159 = 100 + 159 = 259;
2. (247 + 159) – 59 = (159 – 59) + 247 = 100 + 247 = 347.
A – (b + c) = a – b – c – закон віднімання суми від числа.
– Яким законом віднімання користувалася Віка?
2567 – (299 + 567) = 2567 – 567 – 299 = 2000 – 299 = 1701
(a + b) – c = (a – c) + b = a + (b – c) – закон віднімання числа від суми.
При відніманні багатоцифрових чисел користуйтеся способом порозрядного віднімання.
– Чи можна скористатися цим способом, виконуючи віднімання поданих чисел?
1. 325 676 – 27 325;
2. 462 834 – 2944.
324. Обчисліть різницю.
1. 4 ∙ m-n, якщо m = 500, n = 648;
2. 6 ∙ а + b, якщо а = 480? b = 1240.
325. Розв’яжіть рівняння.
8 810 + 30 ∙ х= 13 880 23 860 – х : 13 = 23 660
326. Визначте, на скільки:
1. число 42 001 більше від числа 40 689;
2. число 2092 менше від числа 21 067?
– Перевірте дію віднімання додаванням.
327. На пасіці було 5 повних бочок меду, 5 порожніх і 5 наповнених наполовину. Троє покупців розділили між собою мед так, що кожному дісталась однакова кількість і меду й бочок. Як вони поділили між собою покупку? (Мед не можна перекладати з однієї бочки в іншу).
– Намалюйте малюнок. Розв’яжіть задачу.
Виконайте вдома
328. Знайдіть і запишіть парами вирази з однаковим значенням
780 – (190 + 480) (1426 – 326) – 118
1426 – (326 + 118) 953 – (856 + 44)
329. Яке число позначає кожна буква в квадраті, якщо:
1. А в 2 рази більше, ніж В;
2. В на 25 більше, ніж С;
3. С на 40 менше, ніж Д;
4. Д в 3 рази більше, ніж Е;
5. 1000 в 4 рази більше, ніж Е.

– Зі значення якої букви треба розпочинати пошук?
330. Із 9 м дроту можна виготовити 5 задач-головоломок. Скільки задач-головоломок можна виготовити з 72 дроту?
331. Розгляньте малюнок. Порахуйте трикутники Знайдіть кути: прямий, тупий та гострий. Запишіть їх назви.
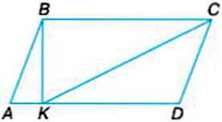
332. Розгляньте таблицю. Кожний рядок – це короткий запис до завдання.
Доданок | Доданок | Сума |
+ 360 | ? | |
-245 | ? | |
+ 321 | ? | |
-570 | ? |
– Що станеться зі значенням суми, якщо перший доданок збільшити на 360, а другий доданок залишити без змін?
– Прочитайте інші запитання. Складіть чотири суми:
600 + 400 = 1000.
– Перевірте свої відповіді.
333. Знайдіть рівності, що відповідають формулі: а + в = с.
A↑ + b = c↑ a + b↓ = c↓
А + b↑ = с↑ a↓ + b = c↓
334. Відомо, що грейпфрут коштує а грн, а ананас на b грн дорожчий. Визначте, у скільки разів грейпфрут дешевше за ананас.
– Розв’яжіть задачу, якщо а = 12 грн, b = 24 грн.
335. Учень купив 3 пензлика та 10 олівців, а учениця – З пензлика і 5 олівців. Учень заплатив за свою покупку 129 грн, а учениця – 99 грн. Яка ціна пензлика?
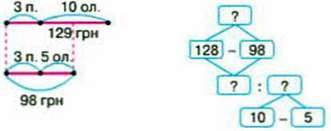
– Розгляньте схеми до умови задачі та й аналізу.
– Поясніть, як міркували, коли їх складали?
– Розв’яжіть задачу.
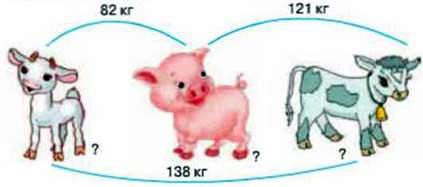
336. Маса козеняти, поросяти й теляти дорівнює 138 кг. Маса козеняти і поросяти – 82 кг, а маса теляти й поросяти дорівнює 121 кг. Визначте масу кожної тварини окремо.
Виконайте вдома
337. Виконайте дії у стовпчик і перевірте їх значення.
36 085 + 14 995 35 306 – 47 539
60 365 + 31 644 587 149 – 89 359
338. Знайдіть змінні величини. Які вони можуть мати значення? Запишіть їх.
1. Час початку занять у школі.
2. Тривалість уроків.
3. Тривалість тижня.
4. Число уроків на день.
5. Число відсутніх.
339. Розгляньте таблицю. Кожний рядок – це короткий запис до завдання.
Зменшуване | Від’ємник | Різниця |
+ 240 | ? | |
-165 | ? | |
+ 150 | ? | |
-130 | ? |
– Що станеться зі значенням різниці, якщо зменшуване збільшити на 240. а від’ємник залишити без змін?
– Прочитайте інші запитання. Складіть чотири різниці:
750 – 200 = 550.
– Перевірте свої відповіді
340. Знайдіть рівності, що відповідають формулі а – b = с:
А↑- b = с↑ а – b↑ = с↓
А – b↓ = с↑ а↓ – b = с↓
341. Поясніть, як знайшли значення змінної.
13 658 + 26 = а
А – 34 = b
B + 82 = с
Перевірка: с – 32 = b + 50.
342. Для екскурсії в театр для учнів замовили 6 автобусів, по 56 місць у кожному автобусі. До театру поїхало 157 хлопчиків. Скільки дівчаток поїхало до театру, якщо всі місця в автобусах були заповнені?
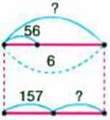
– Розгляньте схему до задачі та записи дітей. Поясніть, як міркували діти.
Соня записала такий вираз:
56 ∙ 6 = 157.
Віка записала свій вираз:
56 ∙ 6 = 157+ х
Виконайте вдома
343. Перевірте дію віднімання додаванням.
9 548 – 3183 5 896 – 3724
344. Обчисліть.
Х + 34 013 = 706 345
345. Довжина огорожі стадіону прямокутної форми становить 960 м. Його ширина на 80 м менша за довжину. Знайдіть довжину та ширину стадіону.
346. Оберіть порядок дій та обчисліть вирази.
1. 31 100 – (4180 ∙ 3 + 2368);
2. 800 ∙ 4 : 20 + 1 ∙ (20 ∙ 7 – 50) + 0 : (33 025 – 25).
347. Першого дня на молокозаводі зварили а кг сиру, а другого – у 4 рази більше. Скільки кілограмів сиру зварили за два дні?
– Складіть вираз до задачі й обчисліть його значення, якщо а = 210.
348. Знайдіть значення букви для кожної нерівності.
23 + r < 25 d – 127 < 130 64 : m < 8
349. До бібліотеки школи № 1 завезли 400 підручників, а в бібліотеку школи № 2 привезли 300 підручників.
– Діти зобразили за допомогою стовпчиків та відрізків кількість підручників у кожній школі.
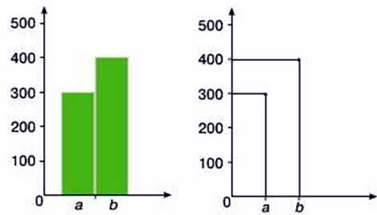
Стовпчаста та лінійна діаграми показують відношення між значенням величин за допомогою висоти стовпчиків чи відрізків. Алгоритм побудови діаграм:
1. дібрати мірку, зручну для зображення значення величин;
2. побудувати шкалу;
3. провести стовпчики (відрізки), довжини яких дорівнюють значенням цих величин.
350. Розгляньте стовпчасту діаграму.
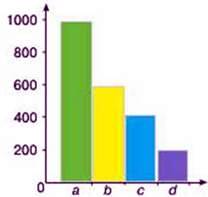
– Визначте вік кожного дерева, а саме: липа – а; клен – b; вишня – с; яблуня – d, де мірка – шкала = 200 років.
– Порівняйте, на скільки довший чи коротший вік кожного з дерев.
351. Побудуйте діаграму кількості відмінників по класах за поданими даними.
4-А кл. – 12 уч. 4-В кл. – 8 уч.
4-Б кл. – 10 уч. 4-Д кл. – 14 уч.
Виконайте вдома
352. Перевірте дію віднімання додаванням.
652 064 – 31 023 83 562 – 21 431
353. Знайдіть значення змінної. Перевірте, чи є ваша відповідь серед чисел, написаних праворуч?
А – 3256 = 93 313
B – а = 27965 b = 124 534; 124 472
354. Сума чисел а + b = 65 968, різниця а – b = 2630.
– Накресліть схеми до рівностей.
– Знайдіть кожне число.
355. Обчисліть і виконайте перевірку.
1001 – 789 359 004 – 27 532 2000 – 1876
4004 – 3999 60 026 – 9 254 7 000 – 1111
356. Виконайте дії: 932 ∙ 79 + (571 – 263) ∙ 64
357. Розгляньте координатний промінь. Назвіть координати точки А Запишіть, де буде місцезнаходження точки А, якщо вона буде рухатися уздовж координатного променя:
1. ліворуч – на 3 мірки;
2. праворуч – на 4 мірки.

358. На координатному промені позначені точки розміщення об’єктів: готель, лікарня, їдальня. 1 мірка на промені становить 8 км.

– Визначте відстань:
1. від готелю до їдальні;
2. від готелю до лікарні;
3. від лікарні до їдальні.
359. Розгляньте таблицю. Кожний рядок – це короткий запис до завдання.
Множник | Множник | Добуток |
+ 3 | ? | |
-6 | ? | |
+ 4 | ? | |
-6 | ? |
– Що станеться зі значенням добутку, якщо перший множник збільшити на 3, а другий залишити без змін?
– Прочитайте інші запитання. Складіть чотири добутки: 10 ∙ 7 = 70 Перевірте свої відповіді.
– Знайдіть рівності, що відповідають формулі а ∙ b = с
A↑ ∙ to = c↑ a↓ ∙ b = c↓
A ∙ b↓ = c↓ a ∙ b↑ = c↑
Виконайте вдома
360. Виконайте дії.
906 ∙ 52 + 568 ∙ 64
361. Накресліть координатний промінь із точками А (5), В (4). Знайдіть відстань між точками, якщо 1 мірка дорівнює 2 см.
362. Розгляньте вирази.
13 258 + 6 239 77 ∙ 20
17 536 – 1243 150 : 3
– Назвіть ознаки, за якими ці вирази об’єднали.
– Знайдіть значення виразів.
– До кожного виразу запишіть обернену дію.
363. Оберіть порядок дій та обчисліть значення виразу.
800 ∙ 4 : 20 + 1 ∙ (20 ∙ 7 – 50) + 0 : (33 025 – 25)
– Поміркуйте Один учень виконав 9 дій. а другий – 6 дій. Результати учні отримали однакові. Чи можливо таке?
364. Розв’яжіть рівняння.
(х – 348) + 5 159 = 12 601 24 957 – (х + 336) = 11 428
365. У вагоні трамвая було х пасажирів. На зупинці з нього вийшло 24 людини, а зайшло у людей. Скільки пасажирів стало у вагоні?
– Знайдіть значення отриманого виразу, якщо х = 62, у = 13
366. Розгляньте таблицю. Кожний рядок – це короткий запис до завдання.
Ділене | Дільник | Частка |
+ 40 | ? | |
-2 | ? | |
+ 2 | ? | |
-20 | ? |
– Що станеться зі значенням частки, якщо ділене збільшити на 40, а дільник залишити без змін?
– Прочитайте інші запитання. Складіть чотири частки: 60 : 4 = 15. Перевірте свої відповіді.
367. Знайдіть рівності, які відповідають формулі а : b = с :
A↑ : b = c↑ а : b↓ = с↑
A↓ : b = с↓ а : b↑ = c↓
368. Побудуйте координатний промінь, 1 мірка якого складає 70 км. Покажіть на ньому рух автомобіля.
– Автомобіль проїхав 5 мірок і зупинився у точці А (11). З якої точки повинен рухатися автомобіль, щоб дістатися в точку А (11)? Скільки кілометрів проїхав автомобіль від початку руху?
Виконайте вдома
369. Оберіть порядок дій та обчисліть вирази.
31 100 – (4180 ∙ 3 + 2368)
370. Знайдіть відстань між точками, які розміщені на координатному промені, 1 мірка якого складає 20 дм.
N і А$ N i В; N i С; В i А, В і С; А i С.

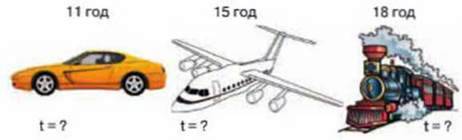
371. Автомобіль, потяг і літак почали рух о 10-00 з міста А до міста Б Літак прибув у місто 6 об 11 годині, потяг – о 15 годині, а автомобіль – о 18годині. Скільки годин кожний об’єкт був у дорозі? Який із об’єктів рухався швидше?
372. Пішохід і велосипедист рухались з міста А в місто Є. Через 1 годину велосипедист дістався пункту Б, а пішохід пройшов лише частину дороги. Скільки часу в дорозі був велосипедист, а скільки – пішохід? Хто з них рухався швидше?
– У такому разі кажуть, що швидкість велосипедиста більша від швидкості пішохода.
Швидкість це відстань, пройдена за одиницю часу.
373. Подумайте й скажіть, чи істинні твердження:
1. що велосипедист проїхав 12 км/год;
2. що пішоход пройшов 5 км/год;
3. що це є їх швидкість, адже кожний із них був у дорозі 1 год.
Швидкість – величина, яка вимірюється такими одиницями:
Кілометр за годину км/год метр за хвилину м/хв
Метр за годину м/год метр за секунду м/с
Позначення одиниць швидкості:
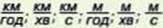
374. Подруги каталися на роликах. Саша пробігла відстань 90 м за 15 с, а Олена – 60 м за 12 с. Хто з дівчат рухався швидше?
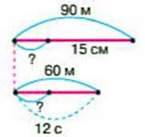
Маша міркувала так: щоб зрозуміти, хто з них рухався швидше, треба порівняти відстань, яку здолали дівчата за 1 с (тобто знайти для кожного мірки).
Розв’язання:
90 : 15 = 6 м за 1 с – швидкість Саші;
60 : 12 = 5 м за 1 с – швидкість Олени.
Відповідь: Саша рухалася швидше.
Запам’ятайте!
У задачах на рух припускаємо, що швидкість (це – мірка) під час руху протягом усього часу не змінюється, а рух відбувається по прямій лінії.
Такий рух називають рівномірним і прямолінійним.
У математиці величини руху позначають латинськими буквами: швидкість – v; відстань – s; час – t.
Формула: v =  установлює взаємозв’язок між величинами, які відображують рух.
установлює взаємозв’язок між величинами, які відображують рух.
S = v ∙ t; t = s : v; v = s : t.
375. Горобець за 1 год пролітає відстань 40 км, а орел за такий ж час пролітає 160 км. Який із птахів швидше здолає шлях 480 км?
Виконайте дома
376. Знайдіть значення виразів зручним способом.
(148 + 245) – 45 894 – (394 + 148)
(473 + 132) – 173 756 + (354 – 256)
843 – (154 + 243) 983 – (787 – 249)
377. Туристи пройшли 15 км за 3 год. З якою швидкістю рухалися туристи?
– Накресліть схему до задачі. Покажіть відстань, швидкість (мірку), час.
– Яка мірка (швидкість) поміститься в числі 15 км 3 рази?
– Оберіть формулу до задачі, запишіть її. Підставте значення букв. Знайдіть відповідь.
378. Виконайте обчислення за діями
(90+5) ∙ 10 + 6325 – 1245
60 + 2 ∙ (100 – 13) ∙ 3
379. Прочитайте одиниці вимірювання. На які множини вони розділені? Виконайте об’єднання цих множин. Дайте назву новій множині.
Година кілометри
Хвилина метри
Секунда сантиметри
Запам’ятайте!
Рух об’єктів можна показати за допомогою таблиць.
Рухомий об’єкт | Швидкість (V) | Час (t) | Відстань (s) |
380. Розв’яжіть задачі, склавши таблицю.
1. Потяг проїхав 336 км за 6 годин. Яка швидкість потяга?
2. Літак пролетів 6400 км за 8 год Яка швидкість літака?
381. Швидкість автомобіля становить 60 км за годину; а швидкість мотоцикла – 40 км за годину. Скільки годин буде в дорозі автомобіль, а скільки мотоцикл, якщо їм потрібно подолати шлях 360 км?
382. Невідоме число збільшили на 189 і отримали число 4206.
– Як зміниться сума, якщо один із доданків збільшити або зменшити на 1205?
– Запишіть ці рівняння та розв’яжіть їх.
383. Один відрізок має довжину 3 м, а другий – довший. Знайдіть довжину другого відрізка, якщо подвоєна сума відрізків дорівнює 14 м.
384. Обчисліть вирази та зробіть перевірку.
25 138 + 26 249
312 514 + 4345
Виконайте вдома
385. Складіть задачу за таблицею. Розв’яжіть її.
Рухомий об’єкт | Швидкість (V) | Час (t) | Відстань (s) |
Велосипедист | 18 км/год | ? | 72 км |
Трактор | 8 км/год | ? | 48 км |
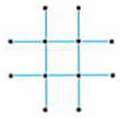
386. Перекладіть 3 палички так, щоб утворилося 3 квадрати.
387. Складіть діаграму швидкостей польоту птахів, якщо відомо, що швидкість польоту:
1. озерної чайки – 50 км/год;
2. сірої ворони – 43 км/год;
3. білого лелеки – 40 км/год;
4. сойки – 35 км/год.
– У якого птаха швидкість найменша?
– На скільки швидкість білого лелеки більша від швидкості сойки?
388. Автомобіль рухався зі швидкістю 70 км/год, а в дорозі був 8 год. Який шлях автомобіль подолав за цей час?
– Складіть таблицю. Розв’яжіть задачу.
– Складіть обернену задачу.
389. Турист проїхав 363 км. Спочатку він плив на катері 6 год зі швидкістю 23 км/год, а залишок шляху пересувався на автобусі зі швидкістю 45 км/год. Скільки годин турист їхав на автобусі?
– Накресліть таблицю.
– Розв’яжіть задачу. Виконайте дії.
390. Напишіть назви всіх трикутників.
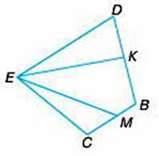
391. Обчисліть.
(300 – 74 ∙ 3) + 76 : 38 998 + (62 403 – 6509)
Виконайте дома
392. Гусениця повзе по стеблу рослини, висота якої 1 м. Удень гусениця піднімається на 4 дм, а вночі опускається на 3 дм. Якого дня гусениця дістанеться вершини стебла?
393. Обчисліть.
837 + 51 : 17 + 6 027
329 ∙ 3 + 85: 17-607
394. Побудуйте діаграму швидкостей руху комах.
1. Кімнатна муха рухається зі швидкістю 6 км/год.
2. Малярійний комар рухається зі швидкістю 4 км/год.
3. Джміль рухається зі швидкістю 3 км/год.
4. Коник рухається зі швидкістю 2 км/год.
– Складіть запитання до побудованої діаграми.
395. Складіть і розв’яжіть пряму й обернені задачі за таблицею.
Рухомий об’єкт | Швидкість (V) | Час (t) | Відстань (s) |
Поїзд | 70 км/год | 72 км |
396. Поїзд проїхав 8 год зі швидкістю 62 км/год. Після цього йому залишилося проїхати до місця призначення у 3 рази більшу відстань, ніж він уже подолав. Яку відстань повинен проїхати поїзд?
397. Напишіть найбільше й найменше п’ятицифрові числа, усі цифри в яких різні. Знайдіть їх суму та різницю.
398. Навесні мама купила 3 порції морозива за 24 грн. Улітку ціна морозива збільшилася на 3 грн. Скільки треба заплатити влітку за 6 порцій такого морозива?
– Зробіть короткий запис до умови задачі, склавши таблицю.
399. Обчисліть
764 + 7 039 – 803 (31 ∙ 2 – 28 ∙ 2) + 296
Виконайте вдома
400. Із поданих фігур побудуйте прямокутник Обчисліть його площу та периметр.

401. Відновіть цифри замість зірочок.
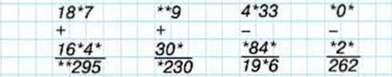
402. Складіть три задачі за даними таблиці.
Швидкість (v) | Чаc (t) | Відстань (s) |
? | 5 год | 400 км |
80 км/год | ? | 240 км |
12 км/год | 4 год | ? |
403. Якщо відома відстань і час руху, то як знайти швидкість?
– Використовуючи дані, складіть задачу. s = 360 км, t = 4, год v=?
– Як зміниться відстань, якщо збільшити час або швидкість?
404. Поїзд проїхав 432 км за 9 год. На скільки треба збільшити швидкість, щоб подолати ту ж саму відстань за 6 год?
– Накресліть таблицю.
– Розв’яжіть задачу
405. Напишіть усі числові значення букв, при яких істинна нерівність.
А ∙ 6 > 42
406. Сторони одного прямокутника – 18 см і 16см. Другий прямокутник має сторони у 2 рази довші. У скільки разів площа другого прямокутника більша за площу першого?
407. Обчисліть.
(5 269 – 4887 + 1609) – (18 001 – 117 993) + 2319.
Виконайте вдома
408. Обчисліть.
1. 527 435 + 11 665 – 57 327;
2. 42 731 – 15 931 – 16 572.
409. Розв’яжіть рівняння, х ∙ 8 + 120 = 280
410. У кошик із грушами поклали 10 яблук. Потім узяли половину всіх фруктів. Після цього в кошику залишилося 17 фруктів. Скільки груш лежало в кошику?
411. Перший автомобіль подолав відстань 560 км за 8 годин, а другий – 560 км за 7 годин. На скільки більша швидкість другого автомобіля, ніж першого?