Головна ⇒ 📌Математика ⇒ Уявлення про десяткові дроби

Уявлення про десяткові дроби

Розділ II ДРОБОВІ ЧИСЛА І ДІЇ З НИМИ

§ 5. ДЕСЯТКОВІ ДРОБИ

Вивчивши матеріал цього параграфа, ви дізнаєтеся, що називають десятковими дробами, що таке відсотки, яке число називають середнім арифметичним кількох чисел. Ви навчитеся порівнювати десяткові дроби, а також виконувати арифметичні дії з десятковими дробами.

30. Уявлення про десяткові дроби

Мабуть, ви помічали, що в буденному житті нерідко доводиться стикатися з величинами, які відрізняються одна від одної в 10, 100, 1000, 10 000 і т. д. разів. Наприклад,

src="/pictures/image538_0.jpg" class=""/>

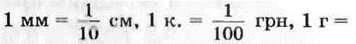
Для дробів, знаменники яких дорівнюють 10, 100, 1000, 10 000 і т. д., придумали зручну, “одноповерхову” форму запису. Пишуть:

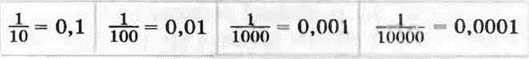
Наведемо ще кілька прикладів:

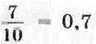(запис 0,7 читають: “нуль цілих сім десятих”);

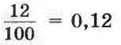(запис 0,12 читають: “нуль цілих дванадцять сотих”);

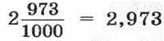(запис 2,973 читають: “дві цілих дев’ятсот сімдесят три тисячних”);

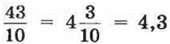(запис 4,3 читають: “чотири цілих три десятих”);

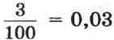(запис 0,03 читають: “нуль цілих

три сотих”);

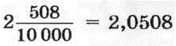(запис 2,0508 читають: “дві цілих п’ятсот вісім десятитисячних”).

Таку форму запису дробів називають десятковою. Дроби, записані в такій формі, називають десятковими дробами. Числа 0,7; 0,12; 2,973; 4,3; 0,03; 2,0508 – приклади десяткових дробів.

У записі десяткового дробу кома відокремлює цілу частину від дробової. Вважають, що ціла частина правильного дробу дорівнює 0. Зверніть увагу на те, що в записі звичайного правильного дробу цілу частину, яка дорівнює нулю, не пишуть, а в записі десяткового дробу – пишуть.

Запис дробової частини десяткового дробу містить стільки цифр, скільки нулів у записі знаменника відповідного звичайного дробу.

Тому, наприклад,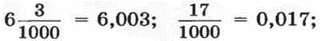

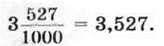
Іноді виникає потреба розглядати натуральне число як десятковий дріб, у якого дробова частина дорівнює нулю. Домовились, наприклад, що 3 = 3,0; 171 = 171,0 і т. д.

Нагадаємо, що десятковий запис натурального числа має таку властивість: одиниця молодшого розряду в 10 разів менша від одиниці сусіднього старшого розряду. Така властивість притаманна й запису десяткових дробів. Отже, одразу після коми йде розряд десятих, далі розряд сотих, потім розряд тисячних і т. д.

Наприклад, наведемо назви розрядів числа 23,70549:

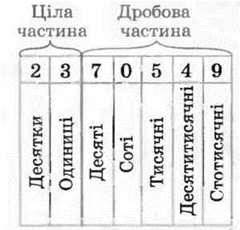
При читанні десяткового дробу спочатку називають його цілу частину, додаючи слово “цілих”, а потім називають дробову частину, додаючи назву останнього розряду. Наприклад, десятковий дріб 23,70549 читають: “двадцять три цілих сімдесят тисяч п’ятсот сорок дев’ять стотисячних”.

ПРИКЛАД 1 Запишіть у вигляді десяткового дробу частку 347 : 100.

Розв’язання. Маємо:

ПРИКЛАД 2 Виразіть у метрах і запишіть у вигляді десяткового дробу: 1) 24 см; 2) 350 см; 3) 5 см; 4) 7 см 2 мм.

Розв’язання. Маємо:

Розв’язуємо усно

1. Яку частину:

1) метра становить: 1 см; 3 дм; 4 мм;

2) тонни становить: 1 кг; 5 ц; 346 кг;

3) квадратного метра становить: 1 дм2; 8 см2?

2. У скільки разів:

1) 1 см менше від їм; 3) 9 м більше за 9 дм;

2) 10 г менше від 1 кг; 4) 4 ц більше за 20 кг?

3. До суми чисел 28 і 6 додайте суму чисел 12 і 14.

4. Від різниці чисел 30 і 16 відніміть різницю чисел 42 і 29.

5. Добуток чисел 12 і 5 помножте на добуток чисел 15 і 4.

6. Частку чисел 90 і 15 поділіть на частку чисел 84 і 14.

7. У саду ростуть 10 яблунь. З першої яблуні Одарка зірвала 1 яблуко, з другої – 2 яблука, з третьої – 3 яблука й т. д., аз десятої – 10 яблук. Скільки всього яблук зірвала Одарка?

Вправи

800.° Запишіть у вигляді десяткового дробу:

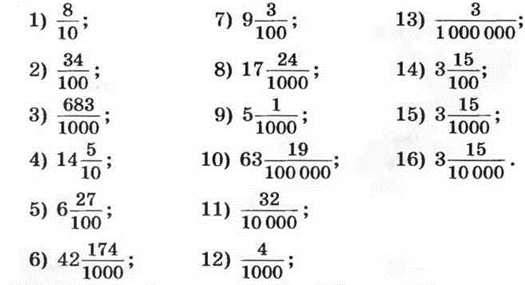
801.° Прочитайте десятковий дріб:

1) 1,6; 4) 6,325; 7) 0,05; 10) 0,0304;

2)12,8; 5)17,4192; 8)0,005; 11) 12,098;

3)5,24; 6) 0,5; 9) 3,04; 12) 0,01012.

802.°Запишіть у вигляді десяткового дробу:

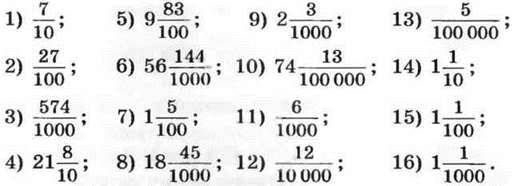
803.° Виділіть цілу та дробову частини числа й запишіть дане число у вигляді десяткового дробу:

804.° Виділіть цілу та дробову частини числа й запишіть дане число у вигляді десяткового дробу:

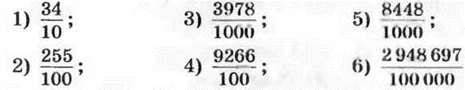
805.° Запишіть число у вигляді звичайного дробу або мішаного числа:

1) 2,4; 4) 1,06; 7) 0,04; 10) 0,001;

2)3,18; 5) 9,074; 8)0,30; 11) 0,072;

3)46,52; 6) 0,9; 9) 0,68; 12) 0,234.

806.° Запишіть число у вигляді звичайного дробу або мішаного числа:

1) 4,9; 3) 1,567; 5) 0,043; 7) 5,06;

2) 8,95; 4) 0,2; 6) 0,008; 8) 12,018.

807.° Запишіть у вигляді десяткового дробу число, у якому:

1) три одиниці, чотири десятих, п’ять сотих;

2) два десятки, вісім одиниць, одна сота, дев’ять тисячних;

3) вісім сотень, дев’ять одиниць, сім десятих, шість тисячних;

4) одна тисяча, одна десятитисячна.

808.° Запишіть у вигляді десяткового дробу число, у якому:

1) дві одиниці, сім десятих;

2) три десятки, дві десятих, вісім сотих;

3) одна сота, три тисячних.

809.° Виразіть у гривнях і запишіть у вигляді десяткового дробу:

1) 64 к.; 2) 5 к.; 3) 4 грн 25 к.; 4) 208 к.

810.° Виразіть у дециметрах і запишіть у вигляді десяткового дробу:

1) 48 см; 3) 8 см 6 мм; 5) 6 мм;

2) 424 см; 4) 64 см 5 мм; 6) 3 см.

811.° Виразіть у кілограмах і запишіть у вигляді десяткового дробу:

1) 1347 г; 3) 382 г; 5) 9 г; 7) 10 кг 6 г;

2) 4256 г; 4) 48 г; 6) 5 кг 24 г; 8) 2 ц 358 г.

812.° Виразіть у метрах і запишіть у вигляді десяткового дробу:

1) 125 см; 3) 4 дм 4 см; 5) 2 см;

2) 18 см; 4) 58 дм 6 см; 6) 4 м 6 дм 5 см.

813.° Запишіть у вигляді десяткового дробу частку:

1) 28 : 10; 4) 2648 : 100; 7) 674 : 1000;

2) 7 : 10; 5) 8351 : 1000; 8) 74 : 1000;

3) 456 : 100; 6) 3590 : 1000; 9) 4 : 1000.

814.° Запишіть у вигляді десяткового дробу частку:

1) 42 : 10; 3) 2484 : 100; 5) 26 435 : 10 000;

2) 35 : 100; 4) 5876 : 10 000; 6) 58 : 1000.

815.° Які числа на координатному промені відповідають:

1) точкам А, В, С, D, Е, F (рис. 202);

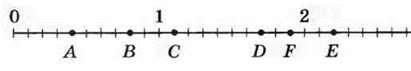
Рис. 202

2) точкам М, N, К, Р, R, S (рис. 203)?

Відповідь запишіть у вигляді десяткових дробів.

Рис. 203

816. Накресліть координатний промінь, узявши за одиничний відрізок, довжина якого в 10 разів більша за сторону клітинки зошита. Позначте на промені точки, що відповідають числам 0,3; 0,7; 0,9; 1,1; 1,5; 2,1.

817. Накресліть координатний промінь, узявши за одиничний відрізок, довжина якого в 10 разів більша за сторону клітинки зошита. Позначте па промені точки, що відповідають числам 0,1; 0,6; 0,8; 1,4; 1,9; 2,2.

Вправи для повторення

818. Мати доручила синові купити продукти. На хліб він витратив 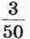усіх грошей, на молоко – 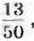на овочі – 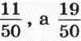усіх грошей – па фрукти. На яку покупку було витрачено найбільше грошей? найменше грошей? Чи залишилися гроші у хлопчика після покупок?

819. У скільки разів 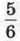хв менше, ніж 1 хв 10 с?

820. У скільки разів 5 год 50 хв більше, ніж 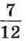год?

821. Які цифри можна підставити замість зірочки, щоб утворилася правильна нерівність:

1) 346* < 3463; 2) 4*40 > 4735?

822. У числах стерли кілька цифр і замість них поставили зірочки. Порівняйте ці числа:

1) 35 ** і 32 **; 2) 98* і *52.

Задана від Мудрої Сови

823. Як розділити порівну 7 яблук між 12 друзями, якщо кожне яблуко можна розрізати не більше ніж на 4 частини?

Коли зроблено уроки

Від шістдесяткових до десяткових дробів

Від виникнення звичайних дробів до винаходу десяткових минули тисячоліття. Винахід десяткових дробів заслужено вважають одним з найважливіших досягнень математичної думки епохи Відродження.

Вам може здатися, що головною властивістю десяткових дробів є їх “одноповерхова” форма запису. Однак річ не стільки в зручній формі запису, скільки у визначній ідеї записувати всі дроби так, щоб їхні знаменники були степенями одного й того самого числа. Ви оціните, наскільки корисною є ця ідея, коли почнете виконувати арифметичні дії з десятковими дробами.

Уже в III тисячолітті до н. е. вавилоняни користувалися дробами, знаменники яких були степенями числа 60. Пізніше шістдесятковими дробами користувалися грецькі та арабські математики. Однак виконувати обчислення, коли натуральні числа записані в десятковій системі, а дроби – у шістдесятковій, було дуже незручно.

Уперше вчення про десяткові дроби виклав у XV ст. самаркандський математик і астроном Джемшид ібн Масуд аль-Каши. Замість коми він використовував вертикальну риску або записував дробову і цілу частини чорнилами різних кольорів.

У 1585 р. фламандський учений Сімон Стевін видав невелику, обсягом усього 7 сторінок, книжку під назвою “Десята”, у якій виклав правила дій з десятковими дробами.

Дещо пізніше (1592 р.) цілу і дробову частини числа стали відокремлювати комою.

Нині в деяких країнах, наприклад у США, замість коми використовують крапку. Звідси походить і використання крапки в комп’ютерних науках та інформаційних технологіях.