Головна ⇒ 📌Математика ⇒ ВІДНОШЕННЯ ТА ЙОГО ВЛАСТИВОСТІ

ВІДНОШЕННЯ ТА ЙОГО ВЛАСТИВОСТІ

Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ

У розділі дізнаєтесь:

Ü про відношення та його властивості;

Ü що таке пропорція;

Ü які є пропорційні залежності величин;

Ü як поділити число в даному відношенні;

Ü що таке масштаб;

Ü про коло, круг, круговий сектор та просторові фігури обертання;

Ü які є види діаграм та як будувати діаграми;

Ü як проводити відсоткові розрахунки;

Ü що таке ймовірність випадкової події та як її знаходити;

Ü як застосувати вивчений матеріал на практиці

§ 12. ВІДНОШЕННЯ

ТА ЙОГО ВЛАСТИВОСТІ

Вам, напевне, доводилося чути фрази: “Шанс перемогти у грі 50 на 50”, “Для приготування гречаної каші крупу і воду треба взяти у відношенні 1 до 2”, “Прибуток поділили, як 3 до 2”. Кожна з цих фраз підводить до порівняння двох чисел: 50 і 50, 1 і 2,

3 і 2. Для цього треба скласти вираз, що є часткою даних чисел, та обчислити його значення. Отже, з першої фрази дістанемо вираз 50 : 50, значення якого дорівнює 1. Це означає, що шанс виграти – такий самий, як і програти. Із другої фрази дістанемо вираз 1 : 2, значення якого становить 0,5. Отже, крупи треба взяти вдвічі менше, ніж води. Поміркуйте

самостійно, як пояснити третю фразу.

Запам’ятайте!

Вираз, що є часткою чисел а і b, відмінних від нуля, називається відношенням чисел а і b.

Записують: а : b або 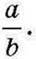Читають: “а відноситься до b”.

Числа а і b називають членами відношення. Якщо виконати ділення першого члена відношення на друге, то дістанемо число, що є значенням відношення. Наприклад, 25 : 2 – відношення чисел 25 і 2, а 12,5 – значення цього відношення.

Відношення показує, які числа порівнюють. Значення відношення показує, у скільки разів перше число більше за друге, або яку частину другого числа становить перше число. Наприклад, значення відношення 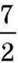показує, що число 7 більше за число 2 у 3,5 раза. А значення відношення 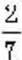Показує частину, яку число 2 становить від числа 7. Відношення 7 до 2 і 2 до 7, які дроби 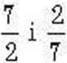, називають взаємно оберненими.

Зверніть увагу:

1) якщо а > b, то значення відношення а до b показує, у скільки разів число а більше за число b:

2) якщо а < b, то значення відношення а до b показує, яку частину числа b становить число а.

Для відношення, як і для будь-якої частки двох чисел, виконуються всі властивості ділення.

Запам’ятайте!

Основна властивість відношення Значення відношення не зміниться, якщо його члени помножити або поділити на одне й те саме число, відмінне від нуля:

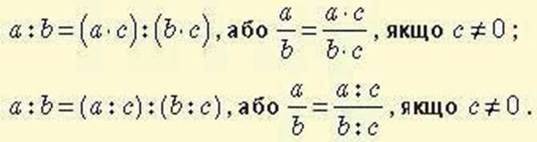
Під час розв’язування задач складають відношення і знаходять їх значення як для однойменних величин, такі для величин з різними найменуваннями.

3адача 1 . Довжина найбільшої риби – луни-риби – становить близько 3 м, а довжина найменшої риби гобі – близько : 16мм. Порівняйте довжини цих риб.

Розв’язання. 1. Можна знайти, у скільки разів довжина луни-риби більш а за довжину риби гобі. Для цього складем о відношення довжини більшої риби до довжини меншої, виразимо ці величини в одних найменуваннях та знайдемо значення відношення:

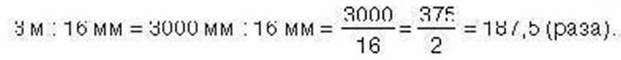
2. Можна знайти, яку частину довжини луни-риби становить довжина риби гобі. Для цього складемо обернене відношення довжин та з найдем о його значення:

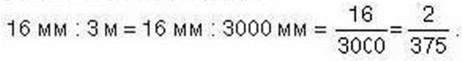
Зверніть увагу:

Значення відношення однойменних величин е числом без найменування.

Задача 2. Знайдіть швидкість гепарда, якщо за 2 с він долає близько 55 м.

Розв’язання. Для знаходження швидкості руху потрібно cкласти відношення відстані до часу руху та обчислити його значення: 55 м : 2 с = 27,5 м/с.

Зверніть увагу:

Значення відношення різнойменних величин є новою величиною, найменування якої відрізняється від найменувань даних величин.

Дізнайтеся більше

Пентаграма (мал. 11) завжди привертала увагу досконалістю форми. Особливість даної фігури полягає в тому, що відношення відрізків, з яких вона складається, мають рівні значення:

AD : АС = АС : CD = АВ : ВС =АD : АЕ = АЕ : ЕС тощо. Давньогрецький математик Піфагор (570-490 pp. до н. е.) та його учні обрали пентаграму символом свого союзу. У наші дні така п’ятикутна зірка прикрашає прапори й герби багатьох країн.

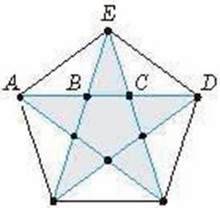
Мал. 11

ПРИГАДАЙМО ГОЛОВНЕ

1. Що називається відношенням двох чисел? значенням відношення?

2. Що показує відношення двох чисел?

3. Які відношення називають взаємно оберненими? Наведіть приклади.

4. Сформулюйте основну властивість відношення.

5. Чому дорівнює значення відношення однойменних величин? різнойменних величин?

РОЗВ’ЯЖІТЬ ЗАДАЧІ

521′. Чи правильно, що відношенням є:

1) число; 2) вираз; 3) рівність; 4) нерівність?

522′. Чи правильно, що значенням відношення є:

1) число; 2) вираз; 3) рівність; 4) нерівність?

523′. Прочитайте відношення:

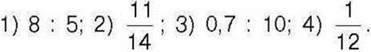
Назвіть члени відношення. Що показує відношення цих чисел?

524′. Чи правильно, що значення відношення не зміниться, якщо його члени;

1) помножити на 2; 4) поділити на 3;

2) збільшити на 2; 5) зменшити на 3;

3) збільшити у 2 рази; 6) зменшити у 2 рази?

525°. Сергійко стверджує, що значенням відношення 15: 10 є число 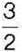, а Петрик – що число 1,5. Хто із хлопців правий?

526°. Чи є число 0,5 значенням відношення:

527°. Знайдіть значення відношення:

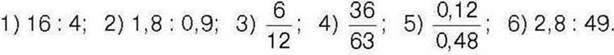
528°. Знайдіть значення відношення:

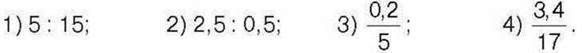
529°. Чи є взаємно оберненими відношення:

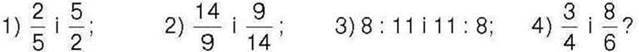
530°. Чи є взаємно оберненими відношення:

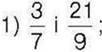2) 5 : 0,2 і 2 : 0,5?

531°. Яке відношення треба вставити замість*, щоб отримати пару взаємно обернених відношень:

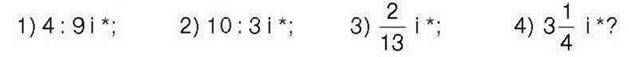
532°. Складіть кілька відношень, значення яких дорівнюють значенню відношення 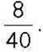Яку властивість ви використали?

533°. Складіть кілька відношень, значення яких дорівнюють значенню відношення 5:15. Яку властивість ви використали?

534°. Чому дорівнює значення відношення:

1)12см:6см; 2)0,2м:5м; 3)4км:60хв; 4)20м:5с?

535°. Чому дорівнює значення відношення:

1)30дм : 5дм; 2) 10м : 2с?

536°. У 6-А класі – 32 учні. Із них – 14 хлопців. У скільки разів дівчат у 6-А класі більше, ніж хлопців? Яку частину учнів класу становлять хлопці, а яку – дівчата?

537°. Мотузку завдовжки 14 м розрізали на дві частини. Довжина першої частини дорівнює 8 м. У скільки разів довжина першої частини більша за довжину другої? Яку частину довжини мотузки становить довжина її першої частини, а яку – довжина другої?

538. Знайдіть значення відношення:

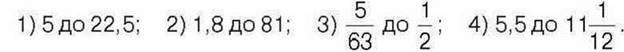
539. Знайдіть значення відношення:

1)45 до 1,5;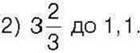

540. Знайдіть швидкість автомобіля, якщо відстань 100 км він проїжджає за: 1) 1 год; 2) 0,8 год; 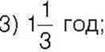4) 30 хв.

541. Перша бригада малярів за 5 год пофарбувала 52 м2 стіни, а друга бригада за 4 год – 43 м2. У якої бригади продуктивність праці вища?

542. Перша бригада кравчинь за 4 дні може пошити 42 костюми, а друга бригада за 6 днів – 63 костюми. У якої бригади продуктивність праці вища?

543. Яке число треба вставити замість а, якщо значення відношення дорівнює 5:

1) а : 2,5;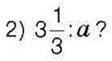

544. Яке число треба вставити замість и, якщо значення відношення дорівнює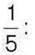

1) 0,8:6;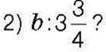

545*. Від мотузки відрізали частину завдовжки 15 м. Знайдіть довжину мотузки, якщо відношення довжини відрізаної частини до довжини мотузки дорівнює 1 : 5.

546*. Два числа відносяться, як 2 : 5. На яке число треба поділити друге число, щоб отримати відношення 2 : З?

547*. Ціна книги знизилась на 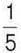її вартості. Чи можна оцінити, у скільки разів попередня ціна вища за нову?

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

548. Поясніть такі фрази: 1) для приготування варення ягід і цукру треба взяти у відношенні 1 до 2; 2) сторони паркану прямокутної форми перебувають у відношенні 1 до 3.

549. Поміряйте довжину і ширину двох кімнату своїй домівці. Знайдіть значення відношення площі підлоги однієї кімнати до площі підлоги іншої кімнати. Який висновок можна зробити за отриманим результатом?

ЗАДАЧІ НА ПОВТОРЕННЯ

550. Складіть числовий вираз і знайдіть його значення: потроїти різницю подвоєної суми чисел 10,5 і 11,4 та добутку чисел 3,5 і 2,8.

551. Сума двох чисел дорівнює 10,5, а їх різниця – 2,5. Знайдіть ці числа.