ВІДОМОСТІ З КУРСУ МАТЕМАТИКИ 5-6 КЛАСІВ
ВІДОМОСТІ З КУРСУ МАТЕМАТИКИ 5-6 КЛАСІВ
Натуральні числа
Числа 1, 2, 3, 4, 5, … , які використовують для лічби предметів, називають натуральними числами. Найменше натуральне число дорівнює 1, найбільше не існує.
При округленні натурального числа до повного розряду всі наступні за цим розрядом цифри замінюють нулями. Якщо перша наступна за цим розрядом цифра 5, 6, 7, 8 або 9, то останню цифру, що залишилася, збільшують на одиницю. Якщо перша наступна за цим розрядом цифра 0, 1, 2, 3 або 4, то останню цифру, яка залишилася, не змінюють.
Наприклад,
4520 ≈ 4500, 17 287 ≈ 17 300, 12 950 ≈ 13 000.
Подільність натуральних чисел
Якщо кажуть, що одне натуральне число дичиться на інше, то мають на увазі ділення без остачі.
Якщо натуральне число а ділиться на натуральне число b, то а називають кратним b, а b – дільником а. Наприклад, число 20 кратне числу 5; число 7 с дільником числа 28.
Ознаки подільності:
1) на 10 діляться всі натуральні числа, запис яких закінчується цифрою 0;
2) на 5 діляться всі натуральні числа, запис яких закінчується цифрою 0 або цифрою 5;
3) на 2 діляться всі натуральні числа, запис яких закінчується парною цифрою;
4)
5) па 9 діляться всі натуральні числа, сума цифр яких ділиться на 9.
Натуральне число називають простим, якщо воно має тільки два дільники: одиницю і саме це число. Натуральне число називають складеним, якщо воно має більше двох дільників.
Наприклад, числа 2, 3, 5, 7, 11 – прості, а числа 4, 6, 15, 108 – складені. Число 1 не є ані простим, ані складеним.
Будь-яке складене число можна розкласти на прості множники. Наприклад:
24 = 2 ∙ 2 ∙ 2 ∙ 3; 120 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 5; 693 = 3 ∙ 3 ∙ 7 ∙ 11.
Найбільше натуральне число, на яке діляться числа а і b, називають найбільшим спільним дільником (НСД) цих чисел.
Щоб знайти НСД двох (або більшої кількості) чисел, треба розкласти ці числа на прості множники і знайти добуток спільних простих множників:

Наприклад, НСД(180; 450) = 2 ∙ 3 ∙ 3 ∙ 5 = 90. Якщо НСД(а; b) = 1, то числа а і b називають взаємно простими.
Найменше натуральне число, яке ділиться на числа а і b, називають найменшим спільним кратним (НСК) цих чисел. Щоб знайти НСК двох (або більшої кількості) чисел, треба розкласти ці числа на прості множники і доповнити розклад одного з них тими множниками інших чисел, яких не вистачає в його розкладі, після чого знайти добуток отриманих множників.
Наприклад,
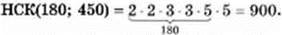
Якщо під час ділення натурального числа а на натуральне число b одержали неповну частку q і остачу r, то а = bq + r, де r < b. Наприклад:

Отже, 108 = 13 ∙ 8 + 4.
Десяткові дроби
З двох десяткових дробів більшим є той, що має більшу цілу частину. Якщо цілі частини дробів рівні, то більший той, у якого більше десятих, і т. д.
Наприклад: 18,7 > 16,92; 12,37 < 12,41; 5,32 > 5,319.
При округленні десяткового дробу до певного розряду всі наступні за цим розрядом цифри замінюють нулями або відкидають (якщо вони стоять після коми). Якщо першою наступною за цим розрядом цифрою є 5, 6, 7, 8 або 9, то останню цифру, що залишилася, збільшують на одиницю. Якщо першою наступною за цим розрядом цифрою є 0, 1, 2, 3 або 4, то останню цифру, що залишилася, не змінюють.
Наприклад, при округленні до сотих маємо:
4,783 ≈ 4,78; 5,925 ≈ 5,93; 4,798 ≈ 4,80.
Додавання і віднімання десяткових дробів викопують порозрядно, записуючи їх один під одним так, щоб кома розташовувалася під комою. Наприклад:
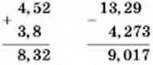
Щоб помножити два десяткових дроби, треба виконати множення, не звертаючи уваги на коми, а потім у добутку відокремити комою праворуч стільки цифр, скільки їх стоїть після коми в обох множниках ралом.
Наприклад:

Щоб помножити десятковий дріб на 10n, де n – натуральне число, треба в цьому дробі перенести кому на n цифр праворуч.
Наприклад: 4,17 ∙ 10 = 41,7; 0,29 ∙ 100 = 29; 4,8 ∙ 1000 = 4800.
Щоб помножити десятковий дріб на 0,1; 0,01; 0,001; … , треба в цьому дробі перенести кому ліворуч на стільки знаків, скільки їх у другому множнику після коми. Наприклад: 7,2 ∙ 0,1 = 1,72; 293 ∙ 0,01 – 2,93; 1,45 ∙ 0,001 = 0,00145.
Щоб поділити десятковий дріб на натуральне число, треба викопати ділення, не звертаючи уваги на кому, але після закінчення ділення цілої частини дробу позначити кому в частці. Наприклад:

Щоб поділити десятковий дріб на 10n, треба в цьому дробі перенести кому на n цифр ліворуч.
Наприклад: 14,5 : 10 = 1,45; 2,37 : 100 = 0,0237.
Щоб поділити десятковий дріб на десятковий, треба в діленому і дільнику перенести коми на стільки цифр праворуч, скільки їх стоїть після коми в дільнику, а потім виконати ділення на натуральне число.
Наприклад: 12,1088 : 2,56 = 1210,88 : 256 = 4,73.
Щоб поділити десятковий дріб на 0,1; 0,01; 0,001, …, треба в цьому дробі перенести кому праворуч на стільки знаків, скільки їх стоїть у діленому після коми.
Наприклад: 4,73 : 0,1 = 47,3; 2,5 : 0,01 = 250; 0,0427 : 0,001 = 42,7.
Звичайні дроби
Частку від ділення числа а на число b можна записати у вигляді звичайного дробу  , дe а – чисельник дробу, b – його знаменник.
, дe а – чисельник дробу, b – його знаменник.
Правильним дробом називають дріб, у якого чисельник менший від знаменника.
Неправильним дробом називають дріб, у якого чисельник більший від знаменника або дорівнює йому.
Значення правильного дробу є меншим за 1, а неправильного – не меншим від 1.
З неправильного дробу можна виділити цілу і дробову частини, тобто перетворити його па мішане число.
Наприклад: 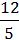 = 2
= 2  ;
; 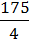 = 43
= 43  .
.
Мішане число можна подати у вигляді неправильного дробу. Наприклад: 4  =
= 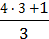 =
= 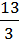 .
.
Основна властивість дробу, значення дробу не зміниться, якщо чисельник і знаменник дробу помножити або поділити на одне й те саме відмінне від нуля число.
Наприклад: 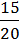 =
= 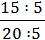 =
=  (скоротили дріб – на 5),
(скоротили дріб – на 5),  =
= 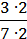 =
= 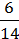 (звели дріб до знаменника 14).
(звели дріб до знаменника 14).
Дроби з однаковими знаменниками додають і віднімають за правилами:
 +
+  =
= 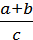 і
і  –
–  =
= 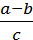 .
.
Наприклад:  +
+  =
=  ;
; 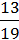 –
– 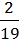 =
= 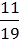 .
.
Щоб додати або відняти дроби з різними знаменниками, їх спочатку зводять до спільного знаменника, а потім виконують дію за правилом додавання або віднімання дробів з однаковими знаменниками.
Наприклад:
5/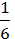 + 3/
+ 3/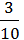 =
= 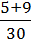 =
= 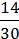 =
= 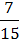 ;
;
3/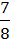 – 2/
– 2/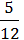 =
= 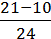 =
= 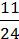 ;
;
Як виконують додавання і віднімання мішаних чисел, показано на прикладах:
55/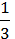 + 23/
+ 23/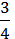 = 7
= 7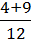 = 7
= 7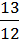 = 8
= 8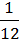 ;
;
74/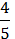 – 65/
– 65/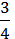 = 1
= 1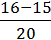 = 1
= 1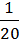 ;
;
54/ – 23/
– 23/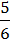 = 3
= 3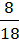 –
– 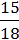 = 2
= 2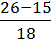 = 2
= 2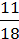 .
.
Добутком двох дробів є дріб, чисельником якого є добуток чисельників цих дробів, а знаменником – добуток знаменників цих дробів:
 ∙
∙  =
= 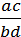
Наприклад:
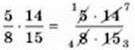 =
= 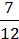 ; 7 ∙
; 7 ∙  =
=  ∙
∙  =
= ∙
∙  =
= 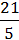 = 4
= 4 = 2
= 2 ∙ 4
∙ 4  =
=  ∙
∙ 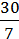 =
= 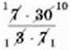 =
=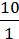 = 10.
= 10.
Два дроби називають взаємно оберненими, якщо їх добуток дорівнює одиниці.
Щоб поділити один дріб на другий, треба ділене помножити на дріб, обернений до дільника:
 :
:  =
=  ∙
∙  =
= 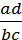 .
.
Наприклад:
 :
: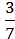 =
=  ∙
∙  =
=  ∙
∙  =
= 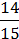 ;2
;2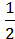 : 1
: 1  =
=  :
:  =
=  ∙
∙ 
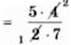 =
= 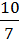 = 1
= 1 .
.
Відношення і пропорції
Частку двох чисел називають відношенням цих чисел.
Приклади відношень: 2 : 7; 0,3 :  Тощо.
Тощо.
Рівність двох відношень називають пропорцією. Наприклад: 8 : 2 = 10 : 2,5 – пропорція.
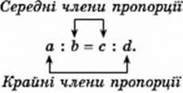
Основна властивість пропорції: добуток крайніх членів пропорції дорівнює добутку її середніх членів, тобто якщо
А : b = с : d (або  =
=  ), то ad = bc.
), то ad = bc.
Дві змінні величини, відношення відповідних значень яких є сталим, називають прямо пропорційними. Якщо дві величини прямо пропорційні, то із збільшенням (зменшенням) значення однієї з них у кілька разів, значення другої величини збільшується (зменшується) у стільки ж разів.
Дві змінні величини, добуток відповідних значень яких є сталим, називають обернено пропорційними. Якщо дві величини обернено пропорційні, то із збільшенням (зменшенням) у кілька разів значення однієї з них у стільки ж разів зменшується (збільшується) відповідне їй значення другої величини.
Додатні і від’ємні числа
Два числа, що різняться лише знаком, називають протилежними числами.
Наприклад: числа 5 і -5 – протилежні.
Модулем числа називають відстань від початку відліку до точки, якою зображено це число на координатній прямій.
Модулем додатного числа і числа нуль є саме це число, а модулем від’ємного числа – протилежне йому число:
Будь-яке від’ємне число є меншим за нуль і меншим за будь-яке додатне число. З двох від’ємних чисел більшим є те, модуль якого менший, і меншим є те, модуль якого більший.
Наприклад: 2 > -10; -5 < 0; -3 < -1; -4 > -15.
Щоб додати два від’ємних числа, треба додати їх модулі і перед одержаним результатом записати знак “-“.
Наприклад: -2 + (-7) = -9.
Щоб додати два числа з різними знаками, треба від більшого з модулів доданків відняти менший модуль і перед результатом записати знак того доданка, модуль якого є більшим.
Наприклад: -7 + 7 = 0; 5 + (-3) = 2; -8 + 1 = -7.
Щоб від одного числа відняти інше, треба до зменшуваного додати число, протилежне від’ємнику:
А – b = а + (-b).
Наприклад: 5 – 9 = 5 + (-9) = -4; -2 – 5 = -2 + (- 5) = -7; -3 – (-7) = – 3 + 7 = 4.
Добуток двох чисел з однаковими знаками дорівнює добутку їх модулів. Добуток двох чисел з різними знаками дорівнює добутку їх модулів, записаному зі знаком “-“. Наприклад: -4 ∙ (-3) =12; 2 ∙ (-5) = -10.
Частка двох чисел з однаковими знаками дорівнює частці їх модулів. Частка двох чисел з різними знаками дорівнює частці їх модулів, записаній зі знаком “-“.
Наприклад: -8 : (-2) = 4; 6 : ( 3) = -2; – 18 : 6 = -3.
Усі цілі числа, усі дробові числа та число 0 називають раціональними числами.
Будь-які раціональні числа мають такі властивості: а + b = b + а – переставна властивість додавання;
(а + b) + с = а + (b + с) – сполучна властивість додавання;
Аb = bа – переставна властивість множення;
(ab)c = а(bс) – сполучна властивість множення;
(а + b)с = ас + bс – розподільна властивість множення.
Перетворення виразів
Щоб звести подібні доданки, треба додати їх коефіцієнти і знайдений результат помножити па спільну буквену частину. Наприклад: 5х + 2х – 7х; 9а – а = 8а; 4b + 7b – 2b = 9b. Щоб розкрити дужки, перед якими стоїть знак “4”, треба не писати дужки і знак “4”, що стоїть перед ними, та записати всі доданки зі своїми знаками.
Наприклад: 4x + (2m – 5р) = 4х + 2m – 5р.
Щоб розкрити дужки, перед якими стоїть знак “-” , треба не писати дужки і знак “-“, що стоїть перед ними, та записати всі доданки з протилежними знаками.
Наприклад: 7х – (5а – 2b) = 7х – 5а + 2b.