Випадкові події та їх імовірності
724.
А) Подія А – випаде 2 очка.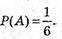 
Б) Подія В – випаде парне число очок: 2, 4, 6,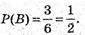 
В) Подія С – випаде число очок, кратне 3: 3, 6.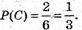 
725.
А) Подія А – 2 очка, це можливо, якщо випаде кісточка доміно
З цифрами 0/2, 1/1. Всього – 28.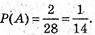 
Б) Подія В: 5 очок: 0/5, 1/4, 2/3 – 3 шт.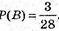 
В) Подія С: 12 очок – це 6/6 – одна подія.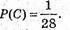 
726.
Подія А – 6 очок на частині кісточки доміно можливо,
6/0, 6/1, 6/2, …,
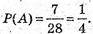
727.
А) Подія А – навмання вибране натуральне одноцифрове число є 7.
Всі можливі результати: 1, 2, 3, 4, 5, 6, 7, 8, 9. Всього 9.
Сприятливих – 1.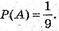 
Б) Подія В – вибране число ділиться на 3; це 3, 6, 9.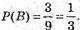 
728.
А) Подія А – зафарбована одна грань.
Всіх кубиків – 8, із зафарбованою одною гранню – 0. Р(А) = 0.
Б) Подія В – зафарбовано 2 грані, таких кубиків немає. Р(В) = 0.
В) Подія С – зафарбовано не менше 3 граней.
Всі 8 кубиків зафарбовано 3 грані, тому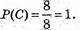 
729.
Якщо пофарбований кубик
То з трьома по фарбованими гранями буде 8 кубиків,
З двома – 24 кубики, з однією 24 кубики і не зафарбованих – 8.
Тому, якщо:
А) подія А – тільки одна зафарбована грань, то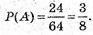 
Б) подія В – рівно 2 грані,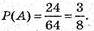 
В) подія С – не менше трьох граней,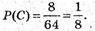 
730.
Якщо пофарбований кубик розрізати на 125 рівних кубиків, то:
З 3 пофарбованими гранями – 8 кубиків
З 2 пофарбованими, гранями – 36 кубиків
З 1 пофарбованою гранню -54 кубики
З 0 пофарбованою гранню – 27 кубиків, тому:
А) подія А – одна пофарбована грань.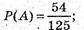 
Б) подія В – 2 пофарбовані грані.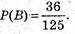 
731.
МАТЕМАТИКА
Всього букв – 10
Буква А – З
Буква М – 2, тому
А) подія А – витягнута буква “А”,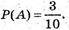 
Б) подія В – витягнута буква “М”,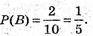 
732.
Простір елементарних подій складається з 8 елементів:
Поява однієї з цифр: 1, 2, З, 4, 5, 6, 7, 8.
А) Подія A – випаде цифра 7.
Цій події сприяє одна елементарна подія.
Тому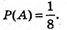 
Б) Подія В – випаде цифра 8, аналогічно.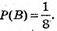 
В) Подія С – цифра 9.
Такої цифри немає на жодній грані октаедра,
Тому Р(С) = 0.
733.
А) Подія А – біла куля.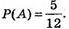 
Б) Подія В – чорна куля.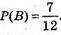 
734.
Подія А – комплект: борщ, котлети, морозиво.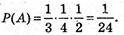 
735.
Подія А – поява числа – “секрету” замка.
Простір елементарних подій: чотирицифрові числа, складені
Із цифр 1, 2, 3, 4, 5, 6. Таких чисел 64 – 1296.
Події А сприяє одне число – “секрет” замка,
Тому імовірність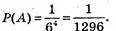
736.
Подія А – книги поставлено в належній послідовності.
Всіх можливих послідовностей 4! – 24.
Тому імовірність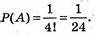
737.
Розв’язання аналогічне № 736.
А – вибрана належна послідовність
Всіх можливих послідовностей 7!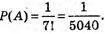 
738.
А) Подія А – перша картка – О; друга – Р; третя – Т.
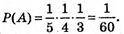
Б) Подія А – з трьох узятих навмання карток можна скласти слово “орт”.
Всіх можливих результатів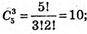
сприятливих – 1;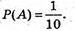 
739.
Подія А – слово “ромб”.
Всіх можливих результатів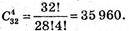
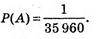
740.
Подія А – із 5-ти конструкцій одна – високої якості.
Всіх можливих результатів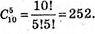
Сприятливих подій А: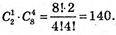 
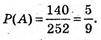
741.
А) Подія А: усі 3 учня – різні мови.
Всіх учнів – 10 + 8 + 6 = 24.
Простір елементарних подій складає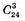 
елементів.
Сприятливих подій 10 × 8 × 6 (по одному учню з кожної групи).
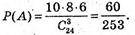
Б) Подія В: уci 3 учні – англійська мова.
Сприятливих подій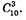
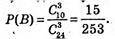
В) Подія С: усі 3 учні вивчають одну з названих мов:
Англійську, німецьку або французьку.
С1 – англійська, С2 – німецька, С3 – французька.
Р(С) = Р(С1) + Р(С2) + Р(С3), оскільки С1, С2, С3 – несумісні події,
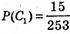(див. б);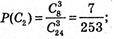 
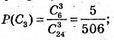
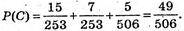
742.
Подія А – із 6 деталей 2 браковані.
6 деталей із 100 можна вибрати способами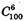
.
Сприятливі результати –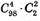
(із 100 деталей – 2 браковані, інші 98 – доброякісні),
Тому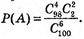 
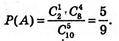
747.
Подія А. – учасник вгадав 3 числа із 49 чисел.
6 чисел – виграшних, 43 – невиграшні.
Будь-які 6 чисел із 49 можна вибрати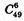
способами.
Це всі можливі результати.
Сприятливі: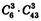 
(3 – виграшних числа, 3 – ні).
Тому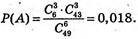 
Подія В – учасник вгадав 4 числа,
Аналогічно,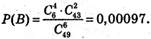 
Подія С – учасник вгадав 5 чисел,
Аналогічно,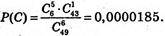 
Подія D – учасник вгадав всі 6 чисел,
Тоді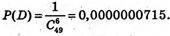 
748.
А)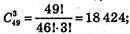 
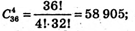
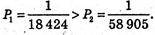3 числа з 49.
Б)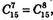 
ймовірності рівні.
В)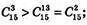 
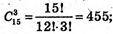
Тому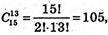 
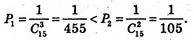
Ймовірність вгадати 3 числа з 15 менша,
Ніж ймовірність вгадати 13 чисел із 15.
(1 votes, average: 5.00 out of 5)
Loading...