Вирази. Числові вирази
Урок № 12
Тема. Вирази. Числові вирази
Мета: систематизувати та узагальнити знання про числові й буквені вирази, набуті учнями в 5-6 класах.
Тип уроку: систематизація та узагальнення знань.
Хід уроку
І. Аналіз тематичної контрольної роботи
Про результати попереднього уроку (тематична контрольна робота № 1) учні дізнаються до уроку (учитель може роздати зошити із тематичної контрольної роботи № 1); аналіз тематичної контрольної роботи учні зробили вдома (отримавши розв’язання роботи у вигляді роздавального матеріалу),
II. Організаційний момент
Учитель інструктує учнів щодо напрямків подальшої роботи (починаємо вивчати нову тему “Вирази”), повідомляє учням термін наступної тематичної контрольної роботи й нагадує, що підготовка до неї починається вже на цьому уроці – повідомляє тему й мету уроку.
III. Актуалізація опорних знань
Виконання усних вправ
1. Виконайте дії: 1) 1,6 + 3,4; 2) 5 – 6,5; 3) 4,2 – 6,2; 4)
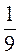 ; 5) 18 :
; 5) 18 : 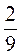 ; 6) (-4) –
; 6) (-4) – 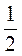 ; 7) (-20) –
; 7) (-20) – 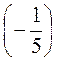 ; 8) 6 :
; 8) 6 : 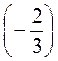 ; 9) 0,52.
; 9) 0,52.2. Серед записів (див. нижче) один зайвий. Знайдіть його й поясніть, чого ви вважаєте його зайвим:
1) 17 – 2 + 8; 2) (14,2 – 11,4) : 4; 3) 42 – 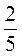 ; 4) (42 – b) – 0,4.
; 4) (42 – b) – 0,4.
3. Розгляньте записи. Встановіть порядок дій і виконайте дії:
1) 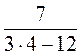 ; 2)
; 2) 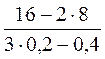 ; 3)
; 3) 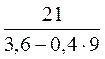 .
.
Яке протиріччя з умовою завдання ви дістали? Чому?
IV. Систематизація та узагальнення знань
Варіант 1. Фронтальна робота з учнями
@ Теоретичні відомості про числові вирази, що повідомляються учням у цій темі, в основному вже відомі їм. З поняттями “числовий вираз”, “значення числового виразу” учні зустрічалися в курсі математики 5-6 класів. Принципово новим для них є поняття числового виразу, що не має змісту. Це поняття буде використано пізніше під час вивчення виразів зі змінними, що не мають змісту при деяких значеннях змінних.
Не зайвим буде пригадати про існування 5-ї арифметичної дії (піднесення до степеня, з яким учні познайомилися ще в 5 класі) та про порядок виконання дій у числовому виразі; не забуваємо про використання властивостей дій в обчисленні значень числових виразів.
Записи в конспектах учнів можуть мати такий вигляд:
Конспект 3 |
Числові вирази |
1. Числові вирази утворюються із чисел, дужок і знаків дій. |
Приклад: 17 – 2 + 8, (14,2 – 11,4) – 4, |
Зауваження. Одне число також вважають числовим виразом. |
Приклад: 7,5; 1 |
2. Значення числового виразу – число, що здобувається після виконання всіх |
Дій у числовому виразі |
Приклад: значенням виразу 17 – 2 + 8 є число 42. |
Зауваження. Не для всіх числових виразів існує їх значення; у цьому випадку кажуть, що вираз не має змісту. |
Приклад: |
|
Варіант 2. Робота із випереджальним домашнім завданням
Враховуючи умову випереджального домашнього завдання, роботу можна організувати так:
На дошці записано таблицю, яку заповнюємо під час фронтальної роботи або після самостійної роботи учнів, коментуючи записи в зошитах:
Відоме | Невідоме |
Після заповнення таблиці повторюємо зміст відомих понять і, використовуючи прийоми роботи з текстом, домагаємось свідомого сприйняття змісту нових понять.
У будь-якому разі після проведеної роботи виконуємо записи в зошитах (конспект 3).
V. Систематизація знань, засвоєння навичок
@ У системі вправ основну увагу приділяємо повторенню алгоритмів дій з раціональними числами; використанню законів дій у ході обчислення значень виразів та вправи, в яких продовжується робота над формуванням важливого математичного вміння переходити від запису числового виразу або виразу зі змінними до його формулювання за допомогою слів і навпаки. Додаткові задачі (№ 4* і 5*) передбачають засвоєння навичок складання числового виразу за певними умовами.
Виконання письмових вправ
1. Знайдіть значення виразів:
1) 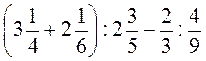 ;
;
2) (-31,7 : 63,4 – 23,4 : (-1,7)) – (-2,4);
3) 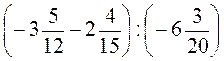 ;
;
4) 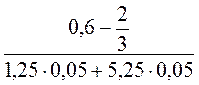 .
.
2. Запишіть числовий вираз і знайдіть значення кожного з них:
1) добуток суми чисел 15 і -22 і числа 2,1;
2) частка різниці чисел 10 і 6,4 і числа -1,2;
3) частка числа 27 і добутку чисел -0,06 і 0,5;
4) добуток суми й різниці чисел 2,7 і 0,3;
5) різниця квадратів чисел 5 і -9;
6) квадрат різниці чисел 1,2 і -0,8.
3. Використовуючи терміни “сума”, “різниця”, “добуток” і “частка”, прочитайте вираз:
1) 8,5 – 7,3; 2) 4,7 – 12,3; 3) 65 : 1,3; 4) 5,6 + 0,9; 5) 2 – 9,5 + 14;
6) (10 – 2,7) : 5; 7) 2,5 – (3,2 + 1,8); 8) 6,1 – (8,4 : 4).
4. Чи мають зміст вирази: 1) 6,3 : (2,5 – 9 – 22,5); 2) (15 – 2,5 – 6) : 4,2?
5*. Використовуючи три рази цифру 2, складіть вираз, значення якого дорівнює: 1) 6; 2) 8; 3) 3; 4) 1.
6*. Складіть числовий вираз для розв’язування задачі:
1) З двох міст, відстань між якими 40 км, вийшли одночасно назустріч один одному два пішоходи. Яка відстань буде між ними через 3 години після виходу, якщо відомо, що швидкість одного пішохода 4 км/год., а другого 5 км/год.?
2) Один робітник виготовляє за годину 7 деталей, а другий – 9 деталей. Скільки деталей вони виготовляють разом за 4 год.?
VI. Рефлексія. Контрольні запитання
1. Наведіть приклад числового виразу і вкажіть, в якому порядку треба виконати дії, щоб знайти його значення?
2. Наведіть приклад числового виразу, що не має змісту.
3. Встановіть відповідність між записами лівого та правого стовпчиків.
1) 3 + 2; 1) сума 3 та 2;
2) 3 – 2; 2) різниця 3 та 2;
3) 3 – 2; 3) квадрат числа 3;
4) 3 : 2; 4) квадрат суми 3 та 2;
5) 32; 5) частка 3 та 2;
6) 23; 6) добуток 3 та 2;
7) (3 + 2)2; 7) сума квадратів 3 та 2;
8) 32 + 22. 8) куб числа 2.
VII. Домашнє завдання
№ 1. Знайдіть значення виразу: 1) 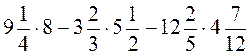 ;
;
2) (-1,2 + 4,32 : (-1,8)) : (-0,001) – (-0,3).
№ 2. Запишіть числові вирази й відшукайте значення кожного з них:
1) частка числа -16 й добутку чисел -0,8 та -0,05;
2) добуток суми й різниці чисел 1,2 і 0,8;
3) різниця квадратів чисел -7 і 8;
4) число, обернене сумі чисел 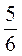 та
та 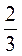 ;
;
5) число, протилежне сумі чисел 2,86 і -4,3.
№ 3. Чи мають зміст вирази: 1) 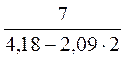 ; 2)
; 2) 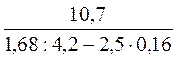 ?
?
№ 4. Випереджальне домашнє завдання.
Порівняйте умови задач (за алгоритмом порівняння).
1) Довжина прямокутної ділянки 42 м, а ширина на 10 м менша. Запишіть вираз для знаходження площі ділянки.
2) Довжина прямокутної ділянки 42 м, а ширина най м менша. Запишіть
Вираз для знаходження площі ділянки.
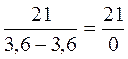 , що обчислити неможливо, тому вираз
, що обчислити неможливо, тому вираз