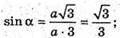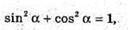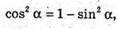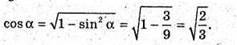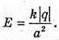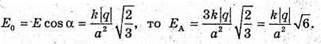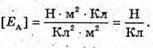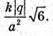Вправа 2
Вправа 2
1. Дано:
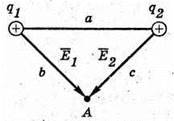
| Розв’язання: “ А) згідно з принципом суперпозиції полів: Оскільки силові лінії спрямовані в один бік, то модуль напруженості результуючого поля: Е = Е1 + Е2 Перевіримо одиниці фізичних величин: Підставимо числові значення: Б) згідно з принципом суперпозиції полів: Оскільки силові лінії протилежно Перевіримо одиниці фізичних величин: Підставимо числові значення: Знак “-” означає, що силові лінії результуючого поля спрямовані в один бік з силовими: лініями другого поля. Отже, В) згідно з принципом суперпозиції полів: Оскільки силові лінії взаємно перпендикулярні, то модуль напруженості результуючого поля знайдемо з паралелограма векторів напруженості Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: а) |
Е – ? |
2. Дано
Q1= 2 ? 10-9 Кл Q2 = -4 ? 10-9 Кл А = 10 см = 0,2 м | Розв’язання: Згідно з принципом суперпозиції полів: Оскільки заряди мають протилежні знаки, то силові лінії спрямовані в один бік. Отже, модуль напруженості результуючого поля дорівнює Е= Е12 + Е2. В точці, що розміщена на відстані Модуль напруженості поля першого заряду: А модуль напруженості поля другого заряду: Отже, Перевіримо одиниці фізичних величин:
Підставимо числові значення:
Відповідь: напруженість поля |
Е – ? |
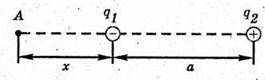
3. Дано: Q1 = -3 ? 10-6 Кл Q2 = 1,2 ? 10-7 Кл A = 12 cm = 0,12 м | Розв’язання: Згідно з принципом суперпозиції полів: Оскільки заряди мають протилежні знаки, то силові лінії спрямовані в один бік. Напруженість результуючого поля буде дорівнювати нулю в точці А, що лежить на лінії, яка проходить через заряди за меншим по модулю зарядом.
Отже, Е1 = – Ег. Модуль напруженості поля першого заряду в точці А:
2х = х + а; 2х – х = а; х = а: х = 0,12 (м). Відповідь: на відстані 12 см за першим зарядом. |
Х – ? |
4 . Дано: Q1 = 2 ? 10-6 Кл Q2 = 1,6 ? 10-7Кл
A = 5 см = 0,05 м B = 3 см = 0,03 м C = 4 см = 0,04 м | Розв’язання:
Згідно з принципом суперпозиції полів: В точці А силові лінії взаємно перпендикулярні. Отже, модуль напруженості результуючого поля в цій точці знайдемо з паралелограма векторів напруженості: Модуль напруженості поля першого заряду в точці А:
Отже, Перевіримо одиниці фізичних величин: Підставимо числові значення:
Відповідь: напруженість електричного поля |
E – ? |
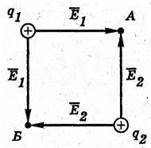
5. Дано: А = 30 см = 0,3 м
Q1 = q2 = 2 ? 10-7 Кл | Розв’язання:
Оскільки заряди кульок однакові, а точки А і Б знаходяться на однаковій відстані, то ЕА = ЕБ = Е. Згідно з принципом суперпозиції полів В точках А і Б силові лінії взаємно перпендикулярні. Отже, модуль напруженості результуючого поля знайдемо з паралелограма векторів Модуль напруженості поля першої кульки А другої Перевіримо одиниці фізичних величин:
Підставимо числові значення:
Відповідь: напруженість поля у вершинах квадрата |
ЕА – ? ЕБ – ? |
6. Дано: Q1 = 16 ? 10-6 Кл Q2 = -24 ? 10-6 Кл А = 10 см = 0,1 м B = 4 см = 0,04 м
| Розв’язання: Точка може знаходитися або між тілами, або за першим тілом. Згідно з принципом суперпозиції полів:
А) Якщо точка знаходиться між тілами, то силові лінії напрямлені в один бік. Отже, модуль напруженості результуючого поля дорівнює: Е = Е1 + Е2. Модуль напруженості поля першого тіла А другого тіла Перевіримо одиниці фізичних величин:
Підставимо числові значення:
Б) Якщо точка знаходиться за першим тілом, то силові лінії напрямлені в різні боки. Отже, модуль напруженості результуючого поля дорівнює Е = Е1 + Е2. Модуль напруженості поля першого тіла
Підставимо числові значення:
Відповідь: якщо точка знаходиться між тілами, то напруженість поля |
E -? |
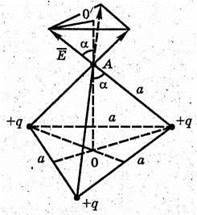
7. Дано: Q1 = q2 = q3 = q | Розв’язання:
Згідно з принципом суперпозиції полів: Спроектуємо вектори напруженості полів кожного із зарядів на вісь ОО1: Знайдемо кут α. Радіус описаного навколо основи кола дорівнює
Модуль напруженості поля одного заряду: Оскільки заряди однакові та знаходяться на однаковій відстані, то модуль напруженості результуючого поля в точці А: ЕА= Е0+ Е0+ Е0=3 Е0 Оскільки Перевіримо одиниці фізичних величин: Відповідь: напруженість поля у вершині тетраедра |
ЕА-? |
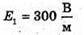
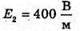
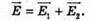
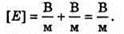
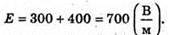
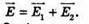
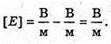
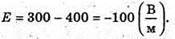
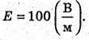
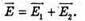
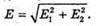
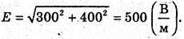
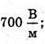 б)
б) 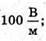 В)
В) 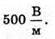
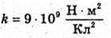
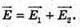
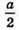 Від зарядів,
Від зарядів,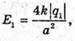
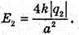
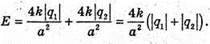
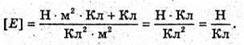
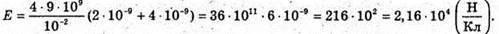
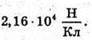
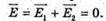
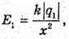 А другого заряду:
А другого заряду: 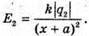
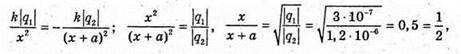
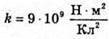
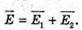
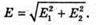
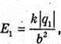 а другого заряду:
а другого заряду: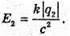
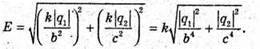
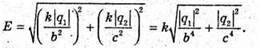
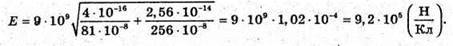
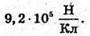
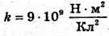
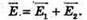
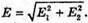
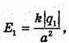
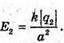 Тоді
Тоді 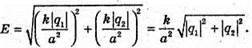
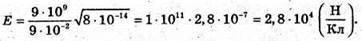
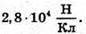
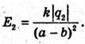
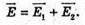
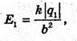
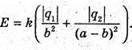
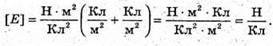
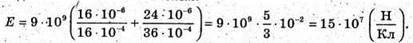
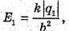 а другого
а другого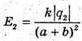 Тоді
Тоді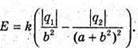
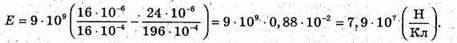
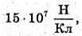 а якщо за першим тілом, то
а якщо за першим тілом, то 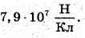
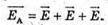
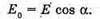
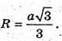 Тоді
Тоді