Головна ⇒ 📌ГДЗ з математики ⇒ Вправи 176-224

Вправи 176-224

176. Якщо три точки лежать на прямій, вони не можуть бути вершинами трикутника.

177.

Вправи 176 224

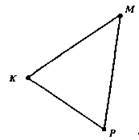
А) Кути прилеглі до сторони МР: ∠KMP і ∠KPM;

Б) ∠KMP – протилежний стороні KP;

В) сторона протилежна куту K – МР;

В) сторони прилеглі до кута Р – KP і РМ.

178. Якщо два трикутники рівні, то їх периметри рівні.

179. Якщо периметри рівні, то трикутники не обов’язково рівні.

180.

Вправи 176 224

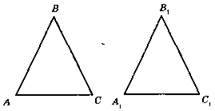
?АВС = ?А1В1С1.

А) ?САВ = ?С1А1В1, так; б) ?АВС = ?А1С1В1, ні, не обов’язково.

181. ?АВС = ?DEF.

1) 3 кутом Е суміститься

∠B;

2) зі стороною АС суміститься сторона DF;

3) ∠C = ∠F;

4) DE = AB.

184.

Вправи 176 224

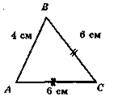
АС = 6 см, AB менша ВС на 2 см, АС = ВС, АС = ВС = 6 см; AB = 6 см – 2 см = 4 см. P? ABC = AB + ВС + АС = 4 см + 6 см + 6 см = 16 см.

Відповідь: 16 см.

185.

Вправи 176 224

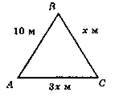
Р? ABC = 24 м; АВ = 10 м; ВС = х м, АС = 3х м;

X + 3х + 10 = 24; 4х = 24 – 10; 4х = 14; х = 3,5; ВС = 3,5 м, АС = 10,5 м. АС – найбільша сторона. Протилежний стороні АС – кут ∠ABC.

186. ?АВС = ?KMN. 1) N = ∠C = 125°;

2) АВ = КМ = 11 см;

3) АВ = 11 см, MN = 8 см, KN = 7 см;

Р? КМN = КМ + MN + KN; КМ = АВ = 11 см;

Р? KMN = 11 см + 8 см + 7 см = 26 (см).

187. ?BAC = ?EFK.

1) EF = AB; ∠K = ∠C; ∠C – найбільший

кут;

2) АВ > ВС > АС; АС – найменша сторона; AC = FK; FK – найбільша сторона? EFK;

3) ?АВС = ?FEK.

188. ?ABC = ?QPR; ∠A = ∠Q, ∠B = ∠P, ∠C = ∠R.

189. ?АВС = ?YZX;AB = YZ, ВС = ZX, AC = YX.

190. ?ABD, ?BDC, ?ADC.

Вправи 176 224

191. ?ABC; AB : ВС : AC = 3 : 5 : 7; BC = 5 мм.

Нехай АВ = 3x, BC = 5x, AC = 7x; 5x = 15; x = 3. AB = 9 мм, BC = 15 мм, AC = 21 мм.

А) P? ABC = 9 + 15 + 21 = 45 (мм);

Б) 3x + 5x + 7x = 60; 15x = 60; x = 4; найменша сторона AB = 3 x 4 = 12 мм;

В) BC – AB = 4 мм; 5х – 3х = 4 мм; 2x = 4 мм; x = 2 мм; найбільша сторона AB = 7x; АС = 7 x 2 = 14 мм.

192.

Вправи 176 224

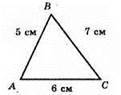
Р? ABC = 18 см; AB + ВС = 12 см, ВС + АС = 13 см;

АВ + ВС + АС = 18; AB + ВС + ВС + АС = 25 см; ВС = 25 – 18 = 7 см; AB = 12 – 7 = 5 см; АС = 18 – 7 – 5 = 6 (см). ВС – найбільша сторона? ABC. Прилеглі кути: ∠B і ∠C.

193. ?АВС = ?DEF = ?KMN; ∠A = ∠D = ∠K = 45°, ∠F = ∠C = ∠N = 80°, ∠M = ∠B = ∠E = 55°.

194. ?АВС = ?DEF = ?KMN; AB = DE = KM = 9 CM; MN = EF = ВС = 8 см; AC = DF = KN = 7 CM; P? DEF = 24; DE + DF + EF = 24; 9 + DF + 8 = 24; DF = 24 – 9 – 8 = 7 (см).

196. У рівних трикутників усі відповідні сторони рівні, отже, і периметри рівних трикутників – рівні.

197. ?АВС = ?KMN; ∠A = ∠N, ∠A = ∠K, ∠C = ∠K, отже, ∠A = ∠C.

198.

Вправи 176 224

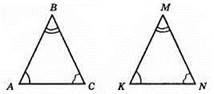
?ABC = ?KMN, ∠K > ∠N; ∠N > ∠M; ∠M – найменший кут; ∠B = ∠M, отже, в? АВС ∠B – найменший кут.

199. ?АВС = ?YXZ.

Вправи 176 224

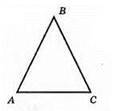
200. ?ABC = ?ZYX.

201.

Вправи 176 224

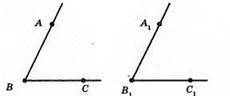
ZB = ZB1, BA = B1A1, BC = B1C1. Відрізки ВС і B1C1 при накладанні сумістяться.

202.

Вправи 176 224

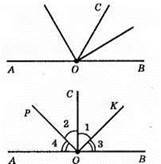
ОР і ОК – бісектриси суміжних кутів ∠AOC і ∠COB. ∠POK – кут між бісектрисами кутів ∠COB і ∠AOC.

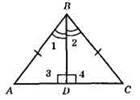
∠1 = ∠2, ∠1 = ∠3, ∠2 = ∠4, отже, ∠1 = ∠2 = ∠3 = ∠4; ∠1 + ∠2 + ∠3 + ∠4 = 180°; ∠1 + ∠3 = ∠2 + ∠4 = 90°. Отже, дані кути – прямі.

203.

Вправи 176 224

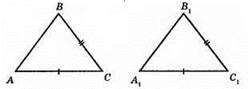
АС = A1C1, ВС = B1C1, ∠BCA = ∠B1C1A1.

204. BC = B1C1.

205.

Вправи 176 224

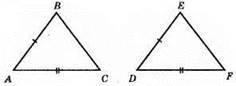
AB = DE, AC = DF, ∠A = ∠E. Що? ABC = ?DEF – не можна стверджувати.

206.

Вправи 176 224

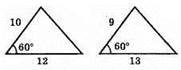
Це твердження неправильне. 10 + 12 = 9 + 13. Суми рівні, а сторони – ні.

207.

Вправи 176 224

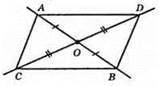
ОА = ОВ, ОС = OD. ?AOC = ?BOD, ∠AOD = ∠BOC за І ознакою рівності трикутників; ∠AOD = ∠COD, ∠AOC = ∠BOD.

208.

Вправи 176 224

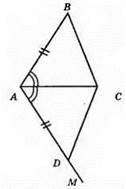
1) AB = AD; 2) ∠CAD = ∠CAB; 3) AC – спільна сторона.

?ABC = ?ADC за першою ознакою рівності трикутників.

209. АВ = А1В1 = 3 см; АС =А1С1 = 8 см; ∠A = ∠A1; ?ABC = ?А1В1С1 за першою ознакою рівності трикутників.

210. 1) AB = AD; 2) ∠BAC = ∠DAC; 3) АС – спільна сторона. ?АВС = ?АDC.

211.

Вправи 176 224

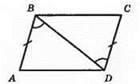
∠ABD = ∠CBD; AB = CD; BD – спільна сторона. ?ABD = ?CBD за першою ознакою рівності трикутників.

212.

Вправи 176 224

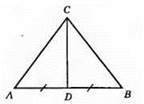
CD ⊥ AB; AD = BD; AD = BD, D – середина відрізка AB; ∠CDA = ∠CDB = 90°; CD – спільна сторона. ?ADC = ?BDC за першою ознакою рівності трикутників.

213.

Вправи 176 224

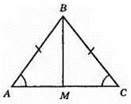
AB = CB; ∠A = ∠C; M – середина AC.

А) AM = MC. ?ABM = ?CBM за першою ознакою рівності трикутників;

Б) ∠CBM = ∠ABM = 25°.

214.

Вправи 176 224

А) Точка С не лежить між точками А і В.

Вправи 176 224

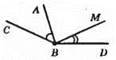
Б) ∠ABC і ∠MBD мають спільну вершину В.

215. а)

Вправи 176 224

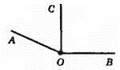
Промінь ОС поділив тупий кут на прямий кут ∠COB і гострий кут ∠AOC.

Б)

Вправи 176 224

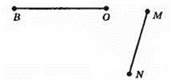
Промені OB і MN не перетинаються і не паралельні.

216.

Вправи 176 224

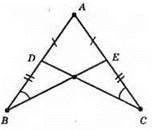
AD = AE; BD = СЕ. Довести: ∠B = ∠C. Доведемо, що? ADC = ?АЕВ.

1) AD = АЕ; 2) AB = АС, AB = AD + BD, АС = АЕ + ЕС; 3) ∠A – спільний кут.

?АDС = ?АЕВ за першою ознакою рівності трикутників.

З рівності трикутників маємо, що всі відповідні елементи рівні, отже, ∠B = ∠C.

217.

Вправи 176 224

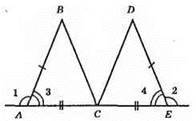
C – середина відрізка AE; AB = DE; ∠1 = ∠2. Доведемо, що BC = DC.

1) AB = DE; 2) AC = CE; 3) ∠3 = ∠4 (кути суміжні рівним кутам ∠1 і ∠2).

?АВС = ?EDC за першою ознакою рівності трикутників. З їхньої рівності маємо: ВС = DС.

218.

Вправи 176 224

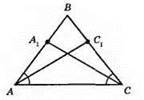
?АВС; ∠A = ∠C; AA1 = СС1; СA1 = 14 см. ?АС1С = СA1A.

1) AС – спільна сторона; 2) AA1 = СС1; 3) ∠A = ∠С. ?AC1С = ?СA1A за першою ознакою рівності трикутників. З їхньої рівності маємо: AC1= СA1 = 14 см.

219.

Вправи 176 224

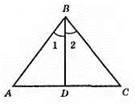
АВ = СВ; ∠ABD = ∠CBD; АС = 8 см. ?ABD = ?CBD (за першою ознакою рівності трикутників). AВ = BC; BD – спільна сторона; ∠1 = ∠2. З рівності трикутників маємо: AD = DC = 4 см.

220.

Вправи 176 224

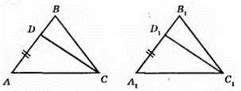
?АВС = ?A1В1С1 (за першою ознакою рівності трикутників). AD = A1D1.

1) AС = AС1; 2) AD = A1D1; 3) ∠A = ∠A1. ?ACD = ?A1С1D1 (за першою ознакою рівності трикутників).

221.

Вправи 176 224

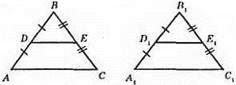
?AВС = ?A1В1С1; BD = A1D1; B1D1 = D1A1; ВЕ = В1Е1; ЕС = Е1С1.

1) BD = B1D1; 2) ВE = В1Е1; ∠В = ∠В1.

?DBE = ∠D1В1E1, за першою ознакою рівності трикутників. Отже, DE = D1Е1.

222. а) МN || AВ;

Вправи 176 224

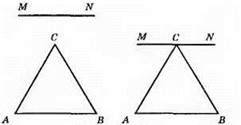
Б) ∠COD + ∠MON = 180°.

Вправи 176 224

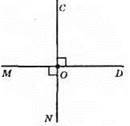
223. а)

Вправи 176 224

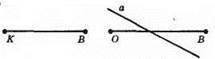
OB || ВK; а перетинає OB, але не перетинає ВК;

Б)

Вправи 176 224

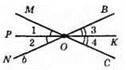
∠1 = ∠2, ∠3 = ∠4, ∠MON ≠ ∠BOC.

224. ?АВС; AB = ВС; ∠1 = ∠2; ?ABD = ?CBD за першою ознакою рівності трикутників.

1) АВ = ВС; 2) BD – спільна сторона; 3) ∠1 = ∠2. 3 цієї рівності маємо: ∠3 = ∠4, а це суміжні кути, ∠3 = ∠4 = 90°. Отже, BD ⊥ AC.

Вправи 176 224


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Вправи 225-273 225. L ⊥ AB; X – точка прямої l; О – середина AB. ?АОХ = ?BOX (за першою ознакою рівності трикутників). 1) АО = OB; 2) ∠3 = ∠4 = 90°; 3) ОХ – спільна сторона. З цього випливає АХ = ВХ, отже, точка X рівновіддалена від кінців відрізка А і В. 226. Три прямі […]...

  2. Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...

  3. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  4. Рівність геометричних фігур Розділ 1. Найпростіші геометричні фігури та їх властивості § 11. Рівність геометричних фігур 397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F. 398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину. 399. Кути ABC і MON сумістити не можна, […]...

  5. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  6. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  7. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  8. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  9. Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ­ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...

  10. Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...

  11. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  12. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  13. Вправи 425-474 425. АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°. Відповідь: 20°, 20°, 140°. 426. […]...

  14. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  15. Перша ознака рівності трикутників Урок № 18 Тема. Перша ознака рівності трикутників Мета: закріпити знання учнями формулювання першої ознаки Рівності трикутників та алгоритму її застосування; формувати навички застосування теореми для розв’язування задач. Тип уроку: засвоєння вмінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Ознаки рівності трикутників”. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Математичний […]...

  16. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  17. Вправи 575-624 575. АВ і АС дотикаються до кола з центром О у точках В і С. ∠CBO = 40°. ?АBО – прямокутний, OB ⊥ AB (OB – радіус, проведений в точку дотику). ?АСО – прямокутний (ОС – радіус, проведений в точку дотику). ∠ABO = 90°; ∠ACO = 90°; ?ВОС – рівнобедрений, OB = ОС; ∠OBC = […]...

  18. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

  19. Вправи для повторення розділу 4 Розділ 4. Коло і круг. Геометричні побудови Вправи для повторення розділу 4 До § 21. 756. AB – діаметр, ОС – радіус. AD – хорда. 757. 1) Коло з променем ОК має одну спільну точку. 2) Коло з прямою ОК має дві спільні точки. 758. ?АОВ = ?ВОС за двома сторонами і кутом між ними […]...

  20. Друга ознака рівності трикутника Урок № 20 Тема. Друга ознака рівності трикутника Мета: домогтися розуміння учнями другої ознаки рівності трикутників та поняття “сторона і прилеглі до неї кути трикутника”. Сформувати в учнів первинні уміння: – знаходити на готових рисунках та в трикутниках, заданих назвою своїх вершин, відповідні сторони і прилеглі до неї кути; – робити висновки щодо рівності трикутників […]...

  21. Вправи 625-682 625. Геометричним місцем центрів кіл радіуса R, що проходить через дану точку А, є коло із центром в точці А і радіусом R. 626. Геометричним місцем центрів кіл, що дотикаються до сторін даного нерозгорнутого кута, є бісектриса даного кута без його вершини О. ОК – бісектриса. 627. Геометричним місцем точок С, які є вершинами трикутників […]...

  22. Коло і круг Розділ 1. Найпростіші геометричні фігури та їх властивості § 15. Коло і круг 588. 1) Хордами є відрізки: KB, NC, KN, CB, LD. 2) Діаметрами є відрізки: LD, NC, КВ. 3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON. 589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK […]...

  23. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  24. Третя ознака рівності трикутників Урок № 26 Тема. Третя ознака рівності трикутників Мета: домогтися розуміння учнями змісту третьої ознаки рівності трикутників та ідеї її доведення; формувати первинні вміння застосовувати третю ознаку рівності трикутників для розв’язування задач. Тип уроку: засвоєння знань. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Ознаки рівності трикутників” (див. урок № 17). ХІД УРОКУ I. Організаційний […]...

  25. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  26. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  27. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  28. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  29. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  30. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ РОЗДІЛ 3 ТРИКУТНИКИ & 12. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ Якщо трикутники ABC і А1В1С1 дорівнюють один одному, то їх можна сумістити. При цьому якщо сумістяться вершини А і А1, В і В1, С і C1, то сумістяться й сторони: АВ з A1B1, ВС з В1С1, СА з C1A1 і кути: ∠A з ∠A1∠B з∠B1, ∠C, ∠C1. […]...

  31. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  32. РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...

  33. Найпростіші задачі па побудову Розділ 1. Найпростіші геометричні фігури та їх властивості § 18. Найпростіші задачі па побудову 708. Щоб побудувати трикутник, що дорівнює трикутнику ABC, треба провести три кола радіусами 5 см, 6 см і 9 см. 709. 710. 1) AС = 5 см; 2) AС = 0,35 дм; 3) AС = 43 мм. 711. 1) Будуємо відрізок […]...

  34. Друга ознака рівності трикутника та її застосування Урок № 21 Тема. Друга ознака рівності трикутників та її застосування Мета: домогтися від учнів свідомого розуміння синтетичної схеми міркувань як одного з основних способів пошуку розв’язання геометричної (і не тільки) задачі; формувати вміння, використовуючи другу та першу ознаки рівності трикутників, застосовувати синтетичний спосіб розв’язування задач на доведення рівності трикутників та задач, що передбачають знаходження […]...

  35. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  36. ТРЕТЯ ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ РОЗДІЛ 3 ТРИКУТНИКИ & 14. ТРЕТЯ ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ Вам уже відомі дві ознаки рівності трикутників. Знаючи властивості рівнобедреного трикутника, можна довести ще одну ознаку. Теорема 18 (третя ознака рівності трикутників). Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам іншого трикутника, то такі трикутники – рівні. Доведення. Нехай у трикутниках ABC і А1В1С1 АВ […]...

  37. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  38. Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...

  39. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  40. Вправи на визначення відмінка прикметника у реченні за відмінком іменника. Контрольна робота: списування. (Вправи 179-181) Тема. Вправи на визначення відмінка прикметника у реченні за відмінком іменника. Контрольна робота: списування. (Вправи 179-181). Мета. Вчити учнів за допомогою відмінкової форми іменників визначати відмінок прикметників у реченнях, виховувати шанобливе ставлення до Батьківщини. Обладнання: вірші, прислів’я про Батьківщину, запис “Пісні про рушник” на сл. А. Малишка, індивідуальні картки з текстом пісні. Хід уроку I. […]...

Ви зараз читаєте: Вправи 176-224
«
»