Вправи 225-273
225.
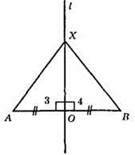
L ⊥ AB; X – точка прямої l; О – середина AB.
?АОХ = ?BOX (за першою ознакою рівності трикутників).
1) АО = OB; 2) ∠3 = ∠4 = 90°; 3) ОХ – спільна сторона.
З цього випливає АХ = ВХ, отже, точка X рівновіддалена від кінців відрізка А і В.
226.
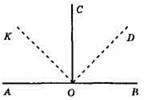
Три прямі кути: ∠AOC, ∠COB, ∠KOD.
227.
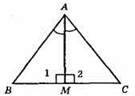
∠AMB = ∠AMC = 90°; ?АМВ = ?АМС; ∠1 = ∠2, ∠1 i ∠2 – суміжні рівні кути.
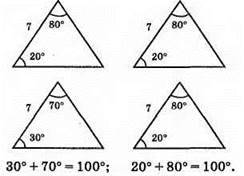
228. Два кути трикутника не можуть бути прямими.
229.
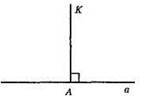
А) Одна
230. а) 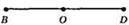
OB і OD – доповняльні промені;
Б) 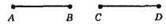
В)
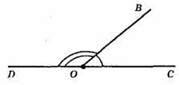
Г)
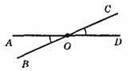
231. а) а || b; 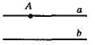
Б) 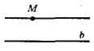
В) 
Г) 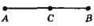
232. AC > AB.
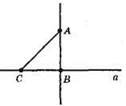
233.
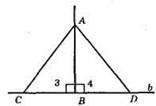
?ABC = ?ABD, AB – спільна, ∠3 = ∠4, BC = BD.
234.
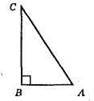
?АВС; ∠В = 90°.
А) Відстань від т. С до прямої AB – ВС;
Б) відстань від т. А до прямої ВС – AB.
235.
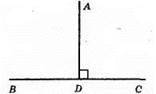
AD –
236. a)
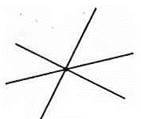
Б)
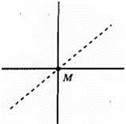
Чотири кути (б) або жодного кута (а).
237.
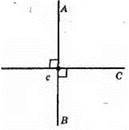
Точки А, В, С лежать на одній прямій. АС – відстань від точки А до прямої с. АС ⊥ с; ВС – відстань від точки В до прямої с. ВС ⊥ с.
238.
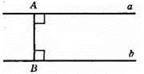
А лежить на прямій а, В лежить на прямій b. AB – відстань відточки А до прямої b і відстань від точки В до прямої а. а || b.
239.
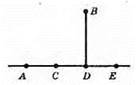
ВD ⊥ AC, ED ⊥ BD.
240.
?ABC = ?KMN.
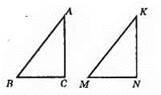
А) Відстань від точки М до прямої MN – це відрізок KN.
Б) Відстань від точки М до прямої KN – це відрізок MN.
241.
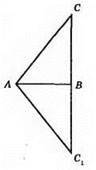
?ABC = ?ABC1.
А) Відстань від точки А до прямої СС1 є відрізок AB.
Б) Відстань від точки С до прямої AB є відрізок ВС.
242.
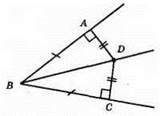
DA – відстань від точки D до сторони AB, DA ⊥ АВ; DC – відстань від точки D до сторони ВС, DC ⊥ ВС.
1) ВА = ВС за умовою; 2) DA = DC; 3) ∠BAD = ∠BCD = 90°.
?ABD = ?CBD, з їх рівності маємо: ∠ABD = ∠CBD, отже, BD – промінь є бісектрисою ∠АВС.
243.
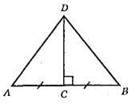
Точка С – середина відрізка AB; DC – відстань від точки D до відрізка AB; DC ⊥ AB.
2) АС = ВС; 2) ∠ACD = ∠BCD = 90°; 3) DC – спільна сторона.
?ADC = ?BDC (за першою ознакою рівності трикутників). З цього маємо: ∠ADC = ∠BDC, DC – бісектриса ∠ADB.
244.
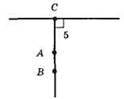
АС = 5 км, ВС = 7 км, ВС – АС = 2 км.
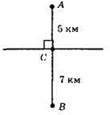
AB =АС + ВС = 5 + 7 = 12 (км).
Відповідь: AB = 2 км або 12 км.
245.
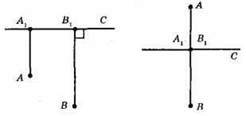
Якщо точки A1 і В1 збігаються, AB ⊥ с. Тобто AA1 ⊥ АС і BB1 ⊥ AC, перпендикуляри мають спільну основу.
246.
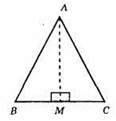
?АВС; М – середина ВС; ∠AMB = ∠AMC; MB = MC; AM – спільна сторона.
?ABM = ?АСМ (за першою ознакою рівності трикутників). Отже, ∠AMB ≠ ∠ACM, бо ∠AMB = ∠AMC; AB = АС; AB і АС – сумістяться, ∠AMB і ∠ACM не сумістяться.
247.
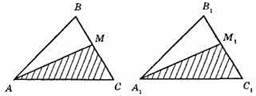
?ABC = ?A1B1C1 = ?АВМ = ?А1В1М1.
1) АС = А1С1; 2) ∠C = ∠C1; 3) ВМ = B1M1 ⇒ CM = C1M1.
Отже, ?AМС = ?A1M1C1 за першою ознакою рівності трикутників.
248.
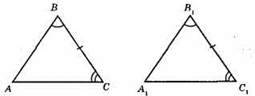
∠B = ∠B1, ∠C = ∠C1, необхідно, щоб BC = B1C1.
249.
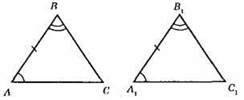
AB = A1B1, ∠A = ∠A1, необхідно, щоб ∠B = ∠B1.
250.
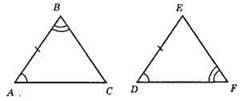
AB = DE, ∠A = ∠D, ∠B = ∠F. Що? ABC = ?DEF не можна стверджувати.
251. Це твердження не зовсім правильне.
252.
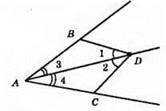
AD – бісектриса, ∠3 = ∠4, ∠1 = ∠2. AD – спільна сторона.
?ABD = ?ACD за другою ознакою рівності трикутників.
253.
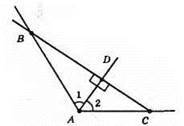
?ABD = ?ACD; ∠1 = ∠2, ∠ADB = ∠ADC = 90°, AD – спільна сторона.
Трикутники рівні за другою ознакою рівності трикутників.
254. АС = А1С1 = 6 см; ∠A = ∠A1; ∠C = ∠C1; ?ABC = ?А1В1С1.
255.
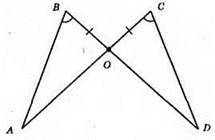
∠B = ∠C; BO = CO; ∠BOA = ∠COA (вертикальні кути).
?АОВ = ?DОС за другою ознакою рівності трикутників.
256.
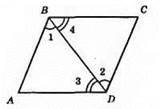
∠ABD = ∠CDB; ∠ADB = ∠CBD; BD – спільна сторона.
?ABD = ?CDB за другою ознакою рівності трикутників.
257.
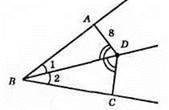
∠ABC; BD – бісектриса; ∠ADB = ∠CDB; ∠ABD = ∠CBD за умовою; BD – спільна сторона.
?ABD = ?CDB за другою ознакою рівності трикутників. З цієї рівності маємо; AD = DC, DC = 8 см.
258.
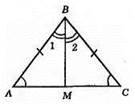
А) ?АВМ = ?CBM. 1) AB = ВС; 2) ∠A = ∠C; 3) ∠ABM = ∠CBM, ВМ – бісектриса кута В.
Б) AM = MC з рівності трикутників? АВМ і? СВМ. ∠BMA = ∠BMC, а це суміжні кути, отже, ∠BMA = ∠BMC = 90°, тому ВМ ⊥ АС.
260.
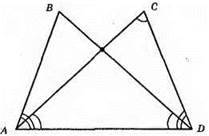
1) ∠BAD = ∠CDA; 2) ∠CAD = ∠BDA; 3) AD – спільна сторона.
?ABD = ?DCA за другою ознакою рівності трикутників.
261.
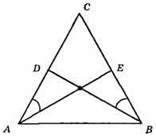
Дано: ?ABC; ∠CAE = ∠CBD; АС = BC. ?BDC = ?АЕС.
1) ∠CAE = ∠CBD; 2) ВС = АС; 3) ∠C – спільний кут.
Трикутники рівні за другою ознакою рівності трикутників. АE = BD – з рівності трикутників.
262.
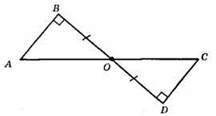
1) BO = OD; 2) ∠B = ∠D = 90°, AB ⊥ BD, DC ⊥ BD; 3) ∠AOB = ∠COD – вертикальні кути.
?AOВ = ?COD за другою ознакою рівності трикутників. АО = 4 см, АО = ОС = 4 см, АС = 8 дм.
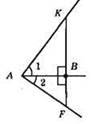
263. АВ – бісектриса ∠A, ∠1 = ∠3, AK = AF, ВК ⊥ AB, ∠KBA = ∠FBA = 90°. ?АВК = ?ABF за стороною Aß (спільна сторона) і двома прилеглими кутами. З рівності трикутників маємо: AK = AF.
264.
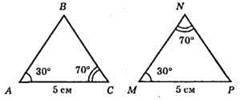
Кути, прилеглі до сторони, повинні бути рівними, тоді трикутники рівні.
Ці трикутники не рівні.
266.
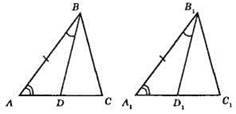
?АВС = ?A1B1C1; ∠ABD = ∠ABD1; 1) AB = A1B1; 2) ∠ABD = ∠A1D1; 3) ∠A = ∠A1.
?ABD = ?A1B1D1 за другою ознакою рівності трикутників. З рівності трикутників маємо: BD = В1D1.
267.
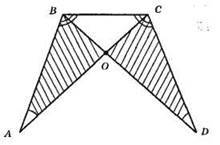
?ABC = ?DCB.
1) AB = CD з рівності трикутників? АВС і? DCB; 2) ∠A = ∠D; 3) ∠ABO = ∠DCO, ці кути доповнюють рівні кути ABC і DCВ. ?ABO = ?DCO за другою ознакою рівності трикутників.
268. ?AOD = ?COF. Доведемо, що? ABE = ?CBD.
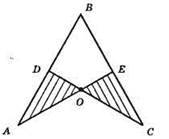
З рівності? AOD і? СОЕ маємо: ∠A = ∠C; EC = AD; OE = OD; AO = OC.
?АВЕ = ?CBD за другою ознакою рівності.
1) ∠A = ∠С; 2) ∠B – спільний кут; 3) АВ = ВС.
269. ?ABC = ?MNK; AB = BC; NK = MK; ∠A = ∠M; ∠B = ∠N; ∠C = ∠K; AB = MN; BC = NK; AC = KM. Із рівності трикутників випливає, що всі сторони рівні.
270. ?ACD, ?BCD.
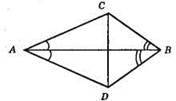
271. Будь – який рівносторонній трикутник є рівнобедреним.
Будь-який рівнобедрений трикутник не завжди є рівностороннім.
272.
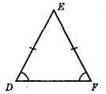
?DEF; DE = EF. Рівні кути: ∠D = ∠F.
273.
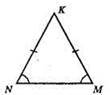
?KMN; ∠M = ∠N. Рівні сторони? KMN; NK = МК.