Вправи для повторення розділу 3
До § 22.
1116. 1) х + 3 = 2; -5 + 3 = 2; -2 ≠ 2; ні;
2) 2 – х = 7; 2 – (-5) = 7; 7 = 7; -5 є коренем рівняння;
3) х : 5 = 1; -5 : 5 = 1; -1 ≠ 1; ні;
4) 4х = -20; х = -20 : 4; х = -5; -5 є коренем рівняння.
1117. 1) х = 2; 2 • (2 – 2) • (2 + 3) = 0; 0 = 0;
2) х = -3; -3 • (-3 – 2) • (-3 + 3) = 0; 0 = 0;
3) х = 0; 0 • (0 – 2) • (0 + 3) = 0; 0 = 0.
Числа 2, -3 і 0 є коренями рівняння.
1118. 1) |х| = 2; х = 2 або х = -2 – корені рівняння;
2) х(х + 2) = 0; х = 0; х + 2 = 0; х = 0; х = -2 – корені рівняння.
Відповідь: рівняння не рівносильні.
2) |x| = 4; х1 = 4 або х2 = -4; 4 і -4 – корені рівняння;
Х2 – 16 = 0; (х – 4)(х + 4) = 0; x = 4; x = -4; 4 і -4 –
Відповідь: рівняння рівносильні.
1119. Це твердження не є правильним.
Х(х – 2) = 0; x = 0 або х = 2;
Х(х2 – 4) = 0; x = 0; x = 2; х = -2.
До § 23.
1120. 1) 7х = -12; х = -12/7; 1 корінь;
2) 0 • x = 0; безліч коренів;
3) -3x = -17; х = 17/3; 1 корінь;
4) 0 • x = 8; немає коренів.
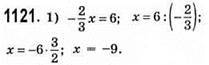
Відповідь: -9.
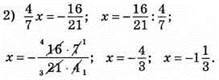
Відповідь: 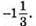
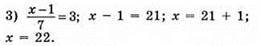
Відповідь: 22.
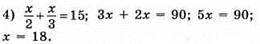
Відповідь: 18.
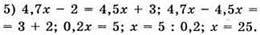
Відповідь: 25.
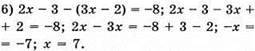
Відповідь: 7.
1122. 1) 10(2x – 7) – 5(4х – 2) = -60; 20x – 70 – 20х + 10
2) 3(5х – 4) – (15х – 2) = 9; 15х – 12 – 15х + 2 = 9; 15х – 15х = 9 – 2 + 12; 0 • х = 19; рівняння не має коренів;
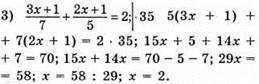
Відповідь: 2.
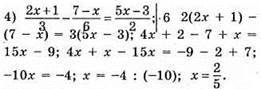
Відповідь: 2/5.
1123. 1) ах = 8. Якщо а = 0, то рівняння 0 • х = 8 не має коренів.
2) (а + 3) • х = а + 3. Коренем цього рівняння є будь-яке число.
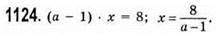
Якщо а = 1, то рівняння не має коренів. Якщо а ≠ 1, то рівняння має один корінь.
До § 24.
1125. x/3 автомобілів відремонтували за день.
1126. Нехай ширина прямокутника х см, тоді його довжина 2х см. Периметр прямокутника становить: 2х + 2 • 2х = 36; 6х = 36; х = 36 : 6; х = 6.
6 см – периметр прямокутника, 12 см – довжина прямокутника. Площа: S = а • b. S = 6 • 12 = 72 (см2).
Відповідь: 6 см; 12 см; 72 (см2).
1127. Нехай один олівець коштує х коп, тоді одна ручка коштує (х + 165) коп.
7х + 3(х + 165) = 1965; 7х + 3х + 495 = 1695; 10х = 1200; х = 1200 : 10; х = 120.
Олівець коштує 1 грн 20 коп; ручка коштує 1 грн 20 коп + 1 грн 65 коп = 2 грн 85 коп.
1128.
Було | Стало | ||
Кошик | X кг. | (х + 1,5) кг | Стало в 3 рази менше |
Ящик | X кг. | (4х – 1,5) кг |
Нехай спочатку у кошику було х кг винограду, а у ящику 4х кг винограду.
(х + 1,5) • 3 = 4х – 1,5; 3х + 4,5 = 4х – 1,5; 3х – 4х = -4,5 – 1,5; – х = -6; х = 6.
У кошику було 6 кг винограду, у ящику було 6 • 4 = 24 (кг) винограду.
1129. Нехай швидкість течії х км/год, швидкість за течією річки (х + 14) км/год, швидкість проти течії річки (14 – х) км/год.
Відстань за течією річки 4,5(х + 14) км, а відстань проти течії 6(14 – х) км. Рівняння:
4,5 • (х + 14) = 6 • (14 – х); 4,5х + 63 = 84 – 6х; 4,5х + 6х = 84 – 63; 10,5х = 21; х = 21 : 10,5; х = 2.
Відповідь: 2 км/год.
1130. Нехай швидкість потяга була х км/год, (х + 15) км/год – швидкість після затримання потягу.
2,5х км поїзд мав пройти відстань за розкладом, а він пройшов цю відстань: 2 • (х + 15) км. Рівняння:
2,5х = 2 • (х + 15); 2,5х = 2х + 30; 2,5х – 2х = 30; 0,5х = 30; х = 30 : 0,5; х = 60.
Відповідь: 60 км/год.
1131.
Було | Забрали | Стало | ||
На першій тарілці | 60 в. | 3х в. | 60 – 3x | У 2 рази менше |
На другій тарілці | 60 в. | Х в. | 60 – x |
Нехай з першої тарілки забрали 3х вареників, а з другої х вареників. Рівняння:
(60 – 3х) • 2 = 60 – х; 120 – 6х = 60 – х; -6х + х = 60 – 120; -5х = -60; х = -60 : (-5); х = 12.
12 вареників забрали з другої тарілки, залишилося 48 вареників; 36 вареників забрали з першої тарілки, залишилося 24 вареники.
Відповідь: 36 вареників, 24 вареники.
1132. Нехай в офісі х працівників. Рівняння:
1100х + 200 = 1200х – 600; 1100х – 1200х = -600 – 200; -100х = -800; х = -800 : (-100); х = 8.
В офісі 8 працівників.
1100 • 8 + 200 = 8800 + 200 = 9000 (грн) – сума премії.
1133.
Було | Продали | Залишилось | ||
І овочева база | 95 кг | 7х кг | 95 – 7х | У 2 рази більше |
II овочева база | 60 кг | 6х кг | 60 – 6x |
Нехай лимони продавали х днів, з першої бази продали 7х кг, з другої 6х кг. Рівняння:
95 – 7х = (60 – 6х) • 2; 95 – 7х = 120 – 12х; -7х + 12х = 120 – 95; 5х = 25; х = 5.
Відповідь: 5 днів.
1134. Нехай першого розчину взяли х г, а другого розчину у т. х + у = 180. У першому розчині було 0,15х г добрива, а в другому – 0,05у г добрива. Всього було 180 • 0,075 = 13,5 г добрива. 0,15х + 0,05 у = 13,5.
Система рівнянь: 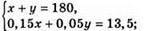
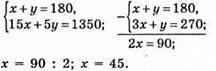
45 г було першого розчину, 180 – 45 = 135 г було другого розчину.
До § 25.
1135. х – у = 6; 7 – 1 = 6. Пара чисел (7; 1) є розв’язком рівняння.
Розв’язки цього рівняння: (10; 4), (6; 0), (8; 2), (0; -6).
1136. 1) 2x + у = 4; у = 4 – 2x.
Розв’язки: (0; 4), (2; 0).
2) х – 3у = 7; x = 7 + 3y.
Розв’язки: (10; 1), (7; 0).
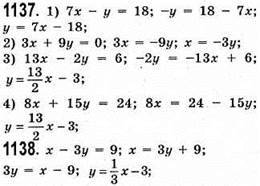
(18; 3), (6; -1), (0; -3), (18; 3) – розв’язки рівняння.
1139. 1) x2 + у2 = -4; x2 + у2 набуває невід’ємних значень;
2) |x| + у2 + 1 = 0; |x| ≥ 0; у2 ≥ 0; |x| + у2 + 1 – додатній вираз при х = 0, у = 0, 1 > 0.
3) -|x| – |у| = 5; -(|x| + |у|) – недодатній вираз;
4) 2×4 + 3|у| = -2; 2×4 + 3|у| – набуває лише невід’ємних значень.
1140. |x| + |у| = 2; (0; 2), (2; 0), (1; 1), (1; -1), (0; -2), (-2; 0), (-1; -1), (-1; 1) – пари чисел є розв’язками рівняння.
1141. 1) x – у = 1; – у = 1 – x; у = x – 1.
X | 0 | 1 |
Y | -1 | 0 |
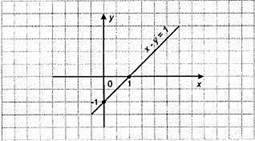
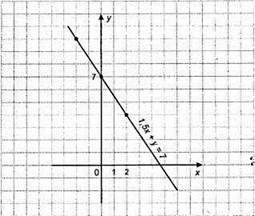
2) 1,5x + у = 7; у = -1,5x + 7;
X | 0 | 2 | -2 |
Y | 7 | 4 | 10 |
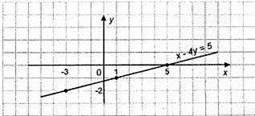
3) х – 4у = 5; -4у = – x + 5; 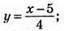
X | 1 | -3 |
Y | -1 | 2 |
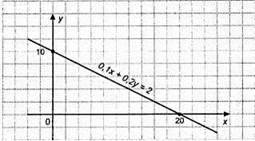
4) 0,1x + 0,2у = 2; x + 2у = 20; 2у = 20 – х; 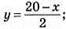
X | 0 | 10 |
Y | 10 | 5 |
1142. х + у = 5;
X | 0 | 5 |
Y | 5 | 0 |
7х – 4у = 2; -4у = 2 – 7х; 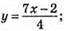
X | 2 | -2 |
Y | 3 | -4 |
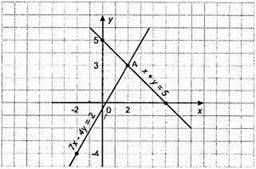
(2; 3) – розв’язок рівнянь; 2 + 3 = 5; 7 • 2 – 4 • 3 = 14 – 12 = 2.
1143. -9х + 5у = 27; у = 0; -9х = 27; х = 27 : (-9) = -3. Абсциса точки: -3.
1144. 1) |x| + y = 0; у = -|x|.
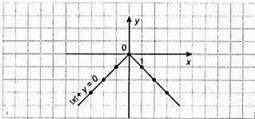
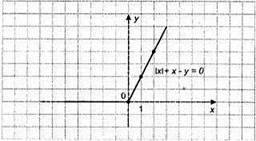
2) |x| + x – у = 0; y = |х| + х;
1) якщо х ≥ 0, у = 2х;
2) якщо х < 0, у = 0.
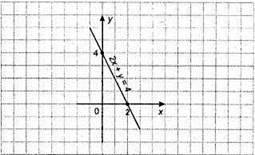
1145. 2х + у = 4; у = -2х + 4;
X | 0 | 1 | 2 |
Y | 4 | 2 | 0 |
До § 27.
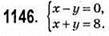 1) х = 5; у = 5;
1) х = 5; у = 5;
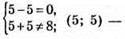 не є розв’язок;
не є розв’язок;
2) х = 4; у = 4;
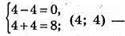 є розв’язок.
є розв’язок.
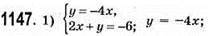
X | 0 | 1 |
Y | 0 | -4 |
2х + у = -6; у = -2х – 6;
X | 0 | -1 |
Y | -6 | -4 |
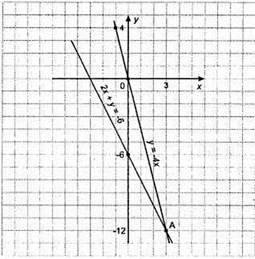
Відповідь: (3; -12).
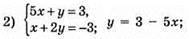
X | 0 | 1 |
Y | 3 | -2 |
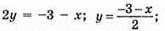
X | 1 | 3 |
Y | -2 | -3 |
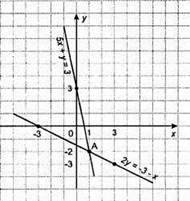
Відповідь: (1; -2).
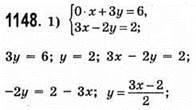
X | 0 | 2 |
Y | -1 | 2 |
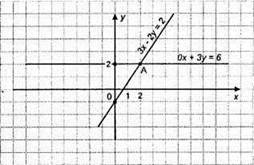
Відповідь: (2; 2).
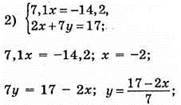
X | -2 | 5 |
Y | 3 | 1 |
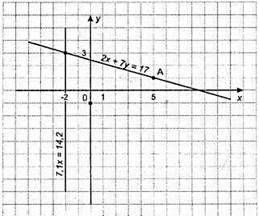
Відповідь: (-2; 3).
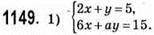
Якщо а = 3, то система має безліч розв’язків.
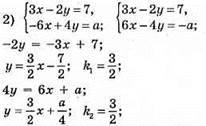
K1 = k2. Система не має розв’язків, якщо а = 14.
До § 28.
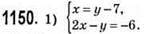
Підставимо х = y – 7 у друге рівняння: 2(у – 7) – y = -6; 2у -14 – у = -6; 2у – у = -6 + 14; у= 8; х = 8 – 7 = 1.
Відповідь: (1; 8).
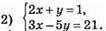
Виразимо з першого рівняння у через х: у = 1 – 2х. Підставимо у друге рівняння:
3х – 5(1 – 2х) = 21; 3х – 5 + 10х = 21; 3х + 10х = 21 + 5; 13х = 26; х = 26 : 13; х = 2.
У = 1 – 2 • 2 = 1 – 4 = -3.
Відповідь: (2; -3).
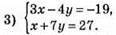
Виразимо із другого рівняння х через у: х = 27 – 7у. Підставимо у перше рівняння:
3 • (27 – 7у) – 4у = -19; 81 – 21у – 4у = -19; -25y = -19 – 81; -25у = -100; у = 4; х = 27 – 7 • 4 = 27 – 28; х = -1.
Відповідь: (1; -4).
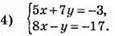
Виразимо у через х: у = 8х + 17. Підставимо в перше рівняння у = 8х + 17.
5х + 7(8х + 17) = -3; 5х + 56х + 119 = -3; 61х = -3,- 119; 61х = -122; х = -122 : 61; х = -2; у = 8 • (-2) + 17 = -16 + 17 = 1.
Відповідь: (-2; 1).
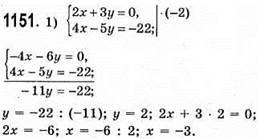
Відповідь: (-3; 2).
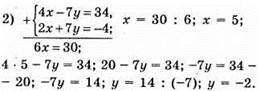
Відповідь: (5; -2).
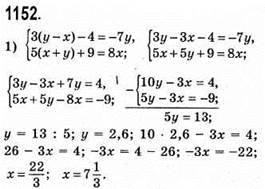
Відповідь: 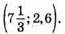
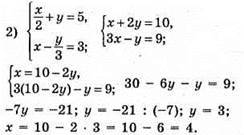
Відповідь: (4; 3).
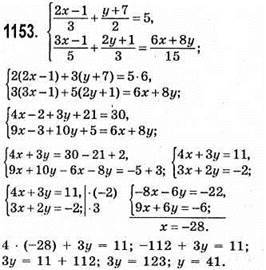
Відповідь: (-28; 41).
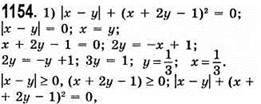
Якщо кожний доданок дорівнює нулю.
Відповідь: (1/3; 1/3).
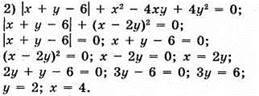
Відповідь: (4; 2).
До § 29.
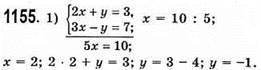
Відповідь: (2; -1).
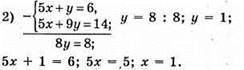
Відповідь: (1; 1).
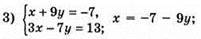
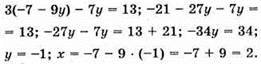
Відповідь: (2; -1).
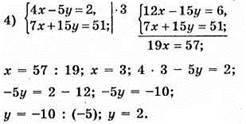
Відповідь: (3; 2).
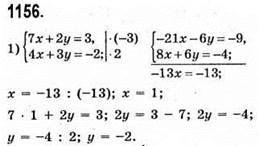
Відповідь: (1; -2).
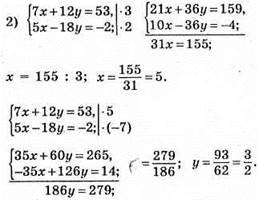
Відповідь: (5; 1,5).
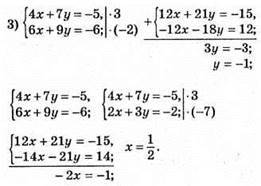
Відповідь: (1/2; -1).
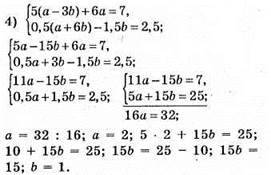
Відповідь: (2; 1).
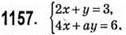
1) Якщо а = 2, система має безліч розв’язків.
2) Якщо а ≠ 2, система має 1 розв’язок.
До §§ 27-29.
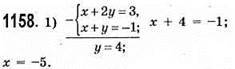
Відповідь: (-5; 4).
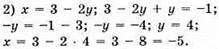
Відповідь: (-5; 4).
У = -1 – х;
X | 0 | -5 |
Y | -1 | 4 |
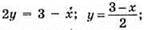
X | 1 | -5 |
Y | 1 | 4 |
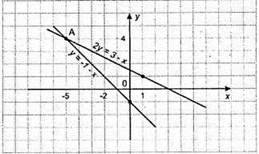
Відповідь: (-5; 4).
2) а) Спосіб підстановки:
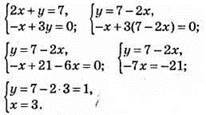
Відповідь: (3; 1).
Б) Спосіб додавання:
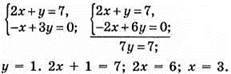
Відповідь: (3; 1).
В) Графічний спосіб: у = 7 – 2х;
X | 0 | 3 |
Y | 7 | 1 |
3у = х; у = 1/3х;
X | 0 | 3 |
Y | 0 | 1 |
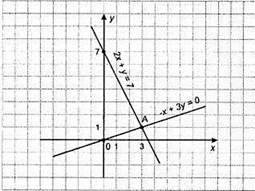
Відповідь: (3; 1).
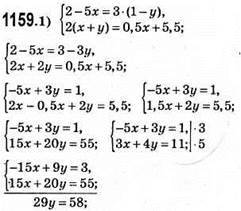

Відповідь: (1; 2).
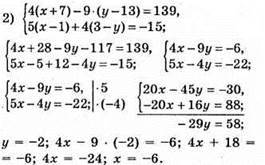
Відповідь: (-6; -2).
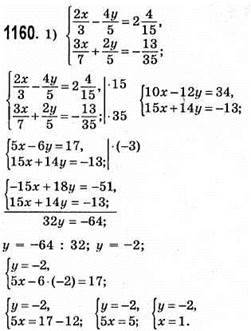
Відповідь: (1; -2).
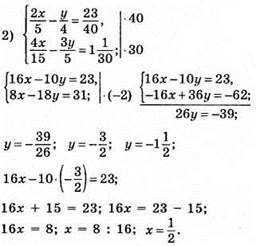
Відповідь: 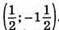
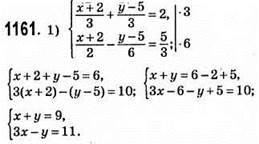
Додамо рівняння: 4х = 20; х = 5; 5 + у = 9; у = 4.
Відповідь: (5; 4).
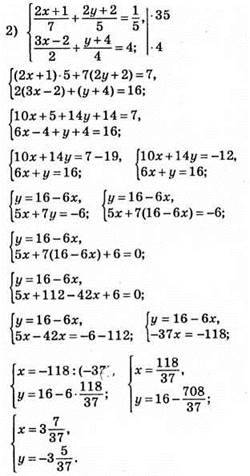
Відповідь: 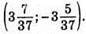
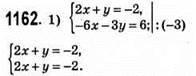
Рівняння має безліч розв’язків.
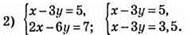
Рівняння не має коренів.
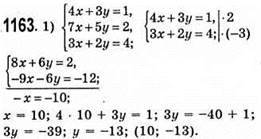
Підставимо пару чисел (10; -13) у рівняння: 7х + 5у = 2;
7 • 10 + 5 • (-13) = 70 – 65 = 5.
Пара чисел (10; -13) не є розв’язком рівняння.
Відповідь: система рівнянь не має розв’язку.
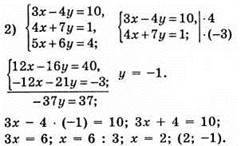
Перевіримо, чи є пара чисел (2; -1) розв’язком рівняння 5х + 6у = 4;
5 • 2 + 6 • (-1) = 10 – 6 = 4.
Відповідь: (2; -1).
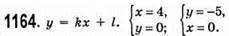
Підставимо координати (4; 0) і (0; -5) у формулу y = kx + l.
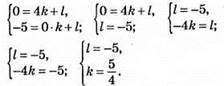
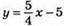 – формула даної функції.
– формула даної функції.
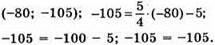
Графік функції 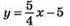 проходить через точку (-80; -105).
проходить через точку (-80; -105).
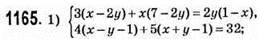
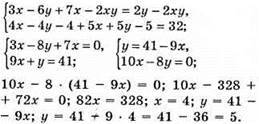
Відповідь: (4; 5).
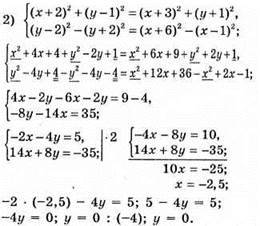
Відповідь: (-2,5; 0).
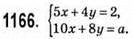
1) Якщо а = 4, то система рівнянь має безліч розв’язків.
2) а ≠ 4, то система рівнянь не має розв’язків.
3) Значення а, при якому система має єдиний розв’язок, не існує.
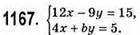
1) b = -3, система має безліч розв’язків.
2) Якщо b ≠ -3, то система має єдиний розв’язок. x = 1,25; у = 0.
До § 30.
1168. Нехай швидкість автобуса x км/год, а швидкість потяга (x + 10) км/год. 3x км турист проїхав на автобусі і 5(х + 10) км проїхав потягом.
3x + 5(x + 10) = 450; 3x + 5x + 50 = 450; 8x = 450 – 50; 8x = 400; x = 400 : 8; x = 50.
50 км/год – швидкість автобуса і 60 км/год – швидкість потяга.
1169. Нехай одна порція млинців коштує x грн, а одна порція салату коштує у грн.
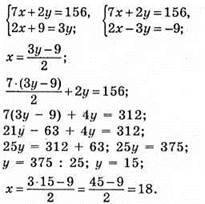
Одна порція млинців коштує 18 грн, а одна порція салату 15 грн.
1170. Нехай власна швидкість x км/ год, а у км/год – швидкість течії; (x + у) км/год – швидкість за течією, (x – у) км/год – швидкість проти течії.
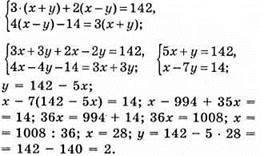
Відповідь: власна швидкість теплохода 28 км/год, швидкість течії 2 км/год.
1171. Нехай майстер за годину виготовляє х деталей, а його учень у деталей.
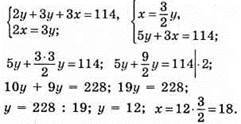
Відповідь: 18 деталей за годину робить майстер, 12 деталей за годину робить учень.
1172. Нехай у першому кошику було х груш, а в другому кошику було у груш.
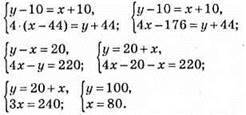
Відповідь: у першому кошику було 80 груш, а в другому кошику було 100 груш.
1173. Нехай одне число х, а друге число у. x/2 – половина числа; 0,75y – частина другого числа.
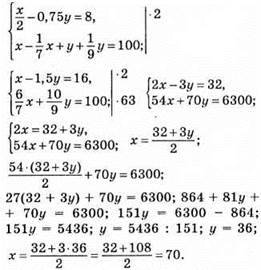
Відповідь: одне число 70, а друге число 36.
1174. Нехай одне число х, а друге 5х, тоді третє число (140 – 6х).
5,75х – стало друге число, а (140 – 6х) • 0,9 – стало третє число.
Рівняння: х + 5,75х + (140 – 6х) • 0,9 = 139,5; х + 5,75х + 126 – 5,4х = 139,5; 5,76x – 5,4х = 139,5 – 126; 1,35х = 13,5; х = 13,5 : 1,35; х = 10.
Одне число 10, друге число 50, а третє число 140 – 60 = 80.
Відповідь: 10, 50, 80.
1175. Нехай х і у – сторони прямокутника, 2(х + у) – периметр прямокутника; х • у – площа прямокутника.
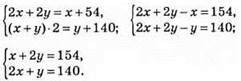
Виразимо з першого рівняння х через у: x = 154 – 2у. Підставимо х у друге рівняння:
2 • (154 – 2у) + у = 140; 308 – 4у + у = 140; -3y = 140 – 308; -3у = -168; у = -168 : (-3); у = 56; х = 154 – 112 = 42.
Площа прямокутника: х • у = 56 • 42 = 2352 (см2).
Відповідь: 2352 см2.
1176. Нехай a i b – цифри двоцифрового числа. 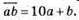
А + b = 8 – сума цифр числа 8. Поміняємо цифри місцями:
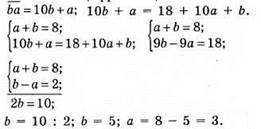
Відповідь: число 35.
1177. Нехай у першому бідоні х л, а у л – у другому бідоні.
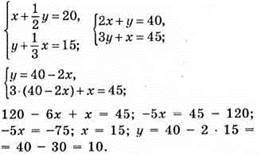
Відповідь: 15 л і 10 л.