ЗАДАЧІ І ВПРАВИ НА ПОВТОРЕННЯ
ПОВТОРЕННЯ
ЗАДАЧІ І ВПРАВИ НА ПОВТОРЕННЯ
Розділ 1. ВИРАЗИ І ТОТОЖНОСТІ
1. Дано числа 4 і 2. Складіть вираз, який є: 1) сумою чисел; 2) різницею чисел; 3) добутком чисел; 4) часткою чисел; 5) степенем, у якого перше число є основою; 6) степенем, у якого перше число є показником. Знайдіть значення цих виразів.
2. Знайдіть значення виразу:
1) 18 – 10 ∙ 1
∙ 1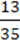 + 6
+ 6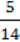 ;
;
2) 5 ∙ 2
∙ 2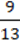 – 1
– 1 : (4
: (4
 );
);3) (3 – 1
– 1 ∙ 5
∙ 5 : (-2,5);
: (-2,5);
4) 0,6 ∙  – (3
– (3 – 2
– 2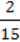 ) : 9,6.
) : 9,6.
3. Обчисліть найбільш раціональним способом:
1) 1,64 ∙ 4,8 + 4,8 ∙ 3,36;
2) 5,32 ∙ 3,1 – 3,32 ∙ 3,1;
3) 3 ∙ 2
∙ 2 ∙ 5 ∙ 7;
∙ 5 ∙ 7;
4)  + 4
+ 4 + 1
+ 1 + 4
+ 4 ;
;
5) (5 +  –
–  ∙ 6;
∙ 6;
6) 5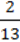 ∙ 5
∙ 5 + 5
+ 5
 .
.4. У 7-А класі навчаються 20 учнів, у 7-Б класі – на 3 учні менше, ніж у 7-А класі, а в 7-В класі – на 5 учнів більше, ніж у 7-Б класі. Скільки учнів навчаються у цих класах разом? Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
5. На першій полиці стоять 15 книг, на другій полиці – на 7 книг менше, ніж на першій полиці, а на третій полиці – стільки книг, як на першій і другій полицях разом. Скільки книг стоять на трьох полицях разом? Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
6. Яке число треба поставити замість зірочки, щоб вираз не мав змісту:
1) 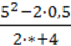 ;
;
2) 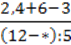 ?
?
7. Знайдіть значення виразу:
1) 12а – 4b + 5, якщо а = -1 , b = 0,25;
, b = 0,25;
2) 0,15c – 14d2 + 4,5, якщо с = -20, d =  .
.
8. Обчисліть значення виразу та заповніть таблицю 30.
Таблиця 30
X | 5 | -10 | 1,2 |
|
Y | 0,2 | 10 | -0,4 | – |
Х + у | ||||
2х + 5 у | ||||
У – x | ||||
|
9. Чи всі значення змінних є допустимими для виразу:
1) 2a – b + 3c;
2) 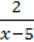 ;
;
3) 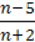 ;
;
4) 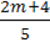 ?
?
10. У числовому виразі 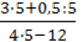 Замініть число 5 на букву а. Чи всі значення змінної а є допустимими для отриманого виразу?
Замініть число 5 на букву а. Чи всі значення змінної а є допустимими для отриманого виразу?
11. Чи є цілим вираз:
1) 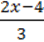 ;
;
2) 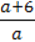 ;
;
3) 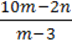 ;
;
4) 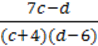 ?
?
12. Одна сторона прямокутника дорівнює а см, а інша – на 4 см більша. Складіть вирази для знаходження периметра і площі прямокутника. Знайдіть значення виразів, якщо:
1) a = 5 см; 2) а = 2,5 см.
13. Складіть вираз для обчислення кількості учнів у 7 класі, в якому навчаються х хлопців та у дівчат. Обчисліть значення цього виразу за даними вашого класу.
14. Спростить вираз і знайдіть його значення:
1) 2,2(а + 5) – 0,4(а – 2,5), якщо а =-5:
2)  (6 – b) + 2(2,5b – 3
(6 – b) + 2(2,5b – 3 ) –
) –  (3,6 – 1,2b), якщо b = 4.
(3,6 – 1,2b), якщо b = 4.
15. Розкрийте дужки і зведіть подібні доданки:
1) 5(3х – 7) –  (10х – 5);
(10х – 5);
2) 4,5x –  8x – 12) – 4 + 2x –
8x – 12) – 4 + 2x –  (x – 6).
(x – 6).
16. За даними значеннями а заповніть таблицю 31.
Таблиця 31
А | 4 | -3,6 |
| – |
А + 1 | ||||
| ||||
4 а | ||||
-3а+ 8 | ||||
|
17. Дано вирази (3х – 4) і (2х + 1). Складіть вираз, який є:
1) сумою виразів; 2) різницею виразів; 3) добутком виразів; 4) часткою виразів. Спростіть отримані вирази та знайдіть їх значення для х = -4.
18. Знайдіть значення виразу 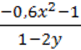 , якщо х = -2, у = -0,4.
, якщо х = -2, у = -0,4.
19. Трицифрове число містить а сотень, b десятків і с одиниць. Складіть і спростіть вираз: 1) сума даного числа і числа, записаного тими самими цифрами в зворотному порядку; 2) різниця даного числа і числа, записаного тими самими цифрами в зворотному порядку.
20. Доведіть, що значення виразу не залежить від х:
1) 5х + (3х – 8(5 + х));
2) 5(х – 12) + 4(6 – х) – (х – 2).
21. Доведіть тотожність за допомогою способу перетворення лівої частини рівності:
1) 10а – (3а – 9b) = 7a + 9b ;
2) (0,5c + d) – 2(0,5d – 0,3c) = 1,1c.
22. Доведіть тотожність за допомогою способу перетворення правої частини рівності:
1) 2y = -1 (x – 9y) + 1
(x – 9y) + 1 X – 9y;
X – 9y;
2) 9m + 1 = 4(m + n) – 5(n – m) + (n + 1).
23. Доведіть тотожність за допомогою способу перетворення обох частин рівності:
1) 10a – 2(3a – 2b) + (2a + b) – (-2a – 3b);
2) (5c + 2) – 0,4(2d + 5) – 0,7d = 7 (c –  D) – 2(c +
D) – 2(c +  D).
D).
24. Доведіть тотожність за допомогою способу різницевого порівняння:
1) 20х – 4(х – 0,5y) = 13х + 3(х – y) + 5у;
2) 5 + (1 N – 2m) –
N – 2m) –  N = (m +
N = (m +  N + 2) – (3m –
N + 2) – (3m –  N – 3).
N – 3).
25. Доведіть тотожність:
1) (а + 1 )(а + 2) – 2 = (а – 3)(а + 4) + 4;
2) 2(3b + 1 )(5 – b) +3 = 50 – 2(b – 1,5)(3b – 1).
Розділ 2. ОДНОЧЛЕНИ
1. Запишіть у вигляді степеня з основою 6:
1)36 ∙ 36; 2)6 ∙ 36 ∙ 216; 3) 36 ∙ 6 ∙ 36 ∙ 36.
2. Запишіть вираз 2 ∙ 4 ∙ 64 ∙ 8 у вигляді степеня з основою:
1)2; 2)4; 3)8; 4) 16; 5) 64.
3. Запишіть вираз 25,6 : 0,25 ∙ 40 у вигляді степеня з основою:
1)2; 2)4; 3)8.
4. Знайдіть:
1) суму квадратів чисел 0,4, -0,3 і -0,5;
2) квадрат суми чисел 0,4, -0,3 і -0,5;
3) різницю квадрата числа 4 і куба числа -2;
4) квадрат різниці кубів чисел 4 і 3.
5. Якими даними треба доповнити порожні клітинки таблиці 32?
Таблиця 32
A | 1 | -1,1 |
| -0,6 |
А2 | ||||
А3 |
6. Знайдіть значення виразу а2 ∙ b3, якщо:
1) а = 15, b = – ; 2) а= –
; 2) а= – , b = -3; 3) а = -0,9, b =
, b = -3; 3) а = -0,9, b =  .
.
7. Порівняйте значення виразів:
1) (-13)13 і 1212; 3) (-1)21 і 112; 5) (-1)22 і 022;
2) (-7)3 і 73; 4) 190 і 199; 6) (-9)7 і (-9)9.
8. Запишіть у вигляді степеня:
1) х4 ∙ х7 ∙ х12;
2) х4 ∙ x6 ∙ х12 ∙ х4 ∙ х;
3) x5 ∙ х7 ∙ х21 : х12 : х4 ∙ х;
4) a ∙ a4∙ a6∙ a ∙ a5;
5) 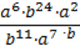 ;
;
6) а6 ∙ a54 : a36 ∙ a : a8.
9. Запишіть у вигляді степеня з основою 8:
1) 168 : 28;
2) 23 ∙ 43;
3)210 ∙ 210 ∙ 210;
4)565 : 75.
10. Запишіть у вигляді степеня:
1) 7 ∙ 0,14 ∙ 72 ∙ 0,16 ∙ 77; 3) 113 ∙ 118 ∙ ( )5 ∙ 0,515 ∙ 119;
)5 ∙ 0,515 ∙ 119;
2) ( )6 ∙ (1
)6 ∙ (1 )8; 4) (1
)8; 4) (1 )12 ∙ (
)12 ∙ ( )5 ∙ 1,26.
)5 ∙ 1,26.
11. Запишіть у вигляді степеня з показником 3:
1) 81 : 33 ∙ 27: 32; 3) 54 ∙ 542 : 183;
2) 99 : 243 ∙ 38; 4) 0,27 ∙ 100 ∙ 93
12. Розв’яжіть рівняння:
1) х6 = 0; 4) (2 – 5х)3 = 0;
2) (х + 8)8 = 0; 5) (6 – х)6 + (х + 4)4 = 0;
3) (-х)7 = 0; 6) (-3 – х)4 + (х + З)4 = 0.
13. Якою цифрою закінчується число:
1) (-555)4 + 651623 + 120125;
2) 1234054 + 1234663 + 521?
14. Обчисліть:
1) (27 ∙ (-9)7 + ( ) ) ∙ (0,2 –
) ) ∙ (0,2 –  )3; 3) – 103 ∙ (-5)2 :((-25)3 ∙ (-22)) ∙ 40;
)3; 3) – 103 ∙ (-5)2 :((-25)3 ∙ (-22)) ∙ 40;
2) (-93)5 : ((-36)3)2; 4) (-304 : ((-6)2)2) : 52.
15. Запишіть у вигляді степеня:
1) (х4)2 ∙ (х5)6 ∙ х3х6 : (х3)10; 6) х4 ∙ ((x6)3)2 – (2х30)3 : (х2)25;
2) (аа5)4 : (a6a4)2; 7) ((-у2)2 ∙ х3)6 ∙ х : (-х4 ∙ y9);
3) (а7)4 ∙ (а6 : а4)2 ∙ (а5 : а4)3; 8) (а2)4 ∙ (а2)6 ∙ (а8)4 : (а11)4;
4) (а44 : а)3 : (а5 : а3)50; 9) 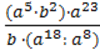
5) (а12а4)3 – (aа5)8; 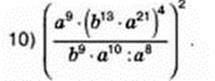
16. За якого натурального значення змінної n виконується нерівність:
1) (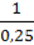 )3 < 4n ≤ -(-2)5 ∙ (-3)4;
)3 < 4n ≤ -(-2)5 ∙ (-3)4;
2)  ≤ 0,5n ≤ 303 : 63 : 500?
≤ 0,5n ≤ 303 : 63 : 500?
17. Обчисліть 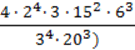
18. Зведіть одночлен до стандартного вигляду:
1) – 0,4 ∙ x15 ∙ 5 ∙ у2 ∙ z ∙ 0,3 ∙ у;
2)  ∙ х3 ∙ у3 ∙ х ∙ у10 ∙ (- 0,12) ∙ х7 ∙ у7 ∙ 10 ∙ х ∙ у2 ∙ у3 ∙ у4.
∙ х3 ∙ у3 ∙ х ∙ у10 ∙ (- 0,12) ∙ х7 ∙ у7 ∙ 10 ∙ х ∙ у2 ∙ у3 ∙ у4.
19. Якими даними треба доповнити порожні клітинки таблиці 33?
Таблиця 33
Одночлен | 1,2ух2 | 4а | 2m | M2n2 | 2,8 | 9а |
Одночлен | 0,5х2 | -3аb | -60m | 3n2 | 5а | 9b |
Сума Одночленів | ||||||
Різниця Одночленів | ||||||
Добуток Одночленів |
20. Якими даними треба доповнити порожні клітинки таблиці 34?
Таблиця 34
Одночлен | У2 | 5,6а | Mnр | -3m2n3 | X3 | -16х2 | 0,02уа |
Одночлен | -уx2 | 4,4а | Рnm | M3n2 | 5х6 | -4х2 | 0,8ух |
Сума одночленів | |||||||
Різниця одночленів | |||||||
Добуток одночленів |
21. Якими даними треба доповнити порожні клітинки таблиці 35?
Таблиця 35
А | -0,3х15у52 | -2а4с9b10 |
| -12p4m12 |
А2 | ||||
А3 |
22. Піднесіть одночлен – а5b4с до степеня, що дорівнює:
1)2; 2)5; 3)100.
23. Зведіть одночлени до стандартного вигляду та знайдіть їх добуток:
1) 0,2х6y15 ∙ (х2)3, -1,5z3 ∙ 6xy5 i -2x15y2;
2) (-у2)6 ∙ (-x4)2, -0,15ху9, – х12у і -0,03(-х)6 ∙ (-у)2.
х12у і -0,03(-х)6 ∙ (-у)2.
24. Зведіть одночлени до стандартного вигляду та знайдіть їх добуток:
1 )-х4n у4 ∙ 5ху2n, 2(хn)2х; 2) (уn+1)8 ∙ (-хn)2, (-ху2)n.
25. Знайдіть натуральні значення n, за яких рівність є правильною:
1) а2n ∙ а5n ∙ (аn)2 = (аа5)3;
2)х2 ∙ х4n ∙ (х2n)3 = х30 : (х ∙ x ∙ (x8)2).
26. З аркуша паперу розмірами 2,4 ∙ 102х2, 4 ∙ 102мм вирізали розгортку куба (мал. 83). Знайдіть об’єм куба.
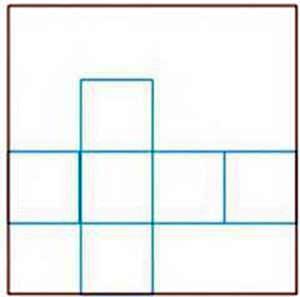
Мал. 83
Розділ 3. МНОГОЧЛЕНИ
1. Спростіть вираз: 1) 2(а6)3 + (а2)9 – (5а5)2 ∙ (-а2)4;
2) b ∙ 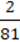 А3 ∙ 93 + аb2 ∙ ас – 18bа3.
А3 ∙ 93 + аb2 ∙ ас – 18bа3.
2. Зведіть подібні члени многочлена:
1) 5,85хy – 8,1х2 – 5 Ху – 0,9х2 – 0,35хy;
Ху – 0,9х2 – 0,35хy;
2) 51ху2 + 13ху – 4ух + 13х2у – 9ху;
3) 7а2 – 26b + 24а – b ∙ 13 – 3а + (-67а) – 5,5а2 – 46а;
4) 14mn – 28mn3 – 3,5nm + (-n)3m.
3. Упорядкуйте за степенями членів многочлен:
1) 7х2 + 3 + х; 2)-4,5 – 2х2 + 67х;
3) 4x + 6×3 + 1 ,8X5 + 3X2 – 2,9; 5) 6ab + 9,7b2a2 + 2b3a + 3,75a;
4) -9,8×4 +  x5 + 5X3 – 0,7X2 – 6; 6)-a22b8 + 6,05b23a25 + 2b15a3 + 3.
x5 + 5X3 – 0,7X2 – 6; 6)-a22b8 + 6,05b23a25 + 2b15a3 + 3.
Який степінь многочлена?
4. Знайдіть суму одночлена і многочлена:
1) – m i m + 5m2; 4) 6х2 і 5х + 0,01;
2) 6k2 i k2 – 3; 5) 0,2х і -5х2 + 15х + 1;
3) – Mn + 4m і 0,2nm; 6) cd і 3 – d + с – 2cd.
Mn + 4m і 0,2nm; 6) cd і 3 – d + с – 2cd.
5. З найдіть добуток двочленів:
1) (12 + х) ∙ (0,2х – 4); 5) (10 + х) ∙ (4х – 1) ∙ (х – 10);
2) (х + 4,5) ∙ (-х – 2); 6) (х2 + 36) ∙ (-х – 6) ∙ (-х + 6);
3) (х2 + х) ∙ (2х + х); 7)(2 – х) ∙ (2х + 1) ∙ (-0,5 + х);
4 (х3 + х2) ∙ (х – 1); 8) (х + 4) ∙ (х – 4) ∙ (х – 5) ∙ (х + 2).
6. Обчисліть значення виразів:
1) (а + 5)5 – а(а + 5), якщо а = 5;
2) ( B + 2) ∙ (3b)2 – (b2 + 10)(-1 + b) – 19(b2 + 1), якщо b = 0,01;
B + 2) ∙ (3b)2 – (b2 + 10)(-1 + b) – 19(b2 + 1), якщо b = 0,01;
3) (х – у)(2х + у) + (у + x)(-x + 2y), якщо х2 + у2 = 16,4.
7. Спростіть вираз і знайдіть його значення:
1) 6а(а + 0,5) – 2(3а2 + а), якщо а = -2,234;
2) (5b2 + b)5 + 10b(b – 0,1) – 4(3b2 + b), якщо b =  ;
;
3) (х – у)(3х + у) – (у + х)(-х + 3у) + 4(у + х)(-х + у), якщо ху = 0,25.
8. Якими даними треба доповнити порожні клітинки таблиці 36?
Таблиця 36
Многочлен | Х – 6 | А + 1 | 0,3 +m2 | A2bc2 – abc2 |
Мночлен | Х + 4 | А2 – а +1 | M – 0,3 | -c2ba – a2bc2 |
Сума | ||||
Різниця | ||||
Добуток |
9. Якими даними треба доповнити порожні клітинки таблиці 37?
Таблиця 37
Многочлен | X3 – y2 | Y3 – 8у2 + 5 | А2 – 2 |
Многочлен | Х3 – х | ||
Сума | 5х3 + 3у2 – 4 | Х3 – х2 + х – 1 | |
Різниця | -y2 + y3 | ||
Добуток | А4 – 4 |
10. Перетворіть вираз у многочлен стандартного вигляду:
1) (1,8а2 + 5,6b2) + (2,09а2- 3b2) – (3,5а2 + 1) – (1 + 0,1b2) – (5а2 – 3,1b2 – 2);
2) (-24а2 + 0,5b2 + 6) – 2(4a2 – 2 B2) + 3(-6a2 + 4 –
B2) + 3(-6a2 + 4 –  B2);
B2);
3) а ∙ а4 – 2 а12 ∙ а5 : а12 + а8 – а2 : а5;
4) (х4)n + (x2n)5 – (х2)3n ∙ х4n + (хn)7 – (-x2)2n.
Знайдіть степінь отриманого многочлена.
11. Перетворіть вираз у многочлен стандартного вигляду:
1) 3(2b +  A)(-b +
A)(-b +  A) – 0,25a(a – 12b); високі дужки
A) – 0,25a(a – 12b); високі дужки
2) ( X – 0,4y) (1
X – 0,4y) (1 X + 9y) – 6y(
X + 9y) – 6y( X – 0,6y);
X – 0,6y);
3) (a2 + ab + b2) (a2 – ab + b2) – (а2 + b2)2 + (ab – 1) (аb + 1);
4) а5n-2 (а2+n)3 – (а2аn)3 : аn+3 – (-a4)2n+1 + а2nа3.
12. Розв’яжіть рівняння:
1) (-x + 8) + (-x – 5) = 21;
2) (9х + 11) – (4х – 8) – (х – 1) = 27;
3) 12 – 3(х – 2) = 4(3 + 2х);
4) 4(4х + 0,5×2) – (2х2 – 5) = 17;
5) (3х + (-x)2 + 2,8) – (x2 + х3) – 12,2 = 2 – х3;
6) (5 + х4 + 6,6 х3) – (х4 – х2 – 3х + 8х3 – 2) = 7 + 3х + х2;
7) (х2 + 5х + 0,25) + (5х2 + 0,75) – (6х2 – 3х) = -1;
8) (4у2 – 5)- (3у2 – 1,25у + 10) – у2 = 2,5.
13. Розв’яжіть рівняння:
1)  Х(0,3х – 2) = 4 + 0,12х2;
Х(0,3х – 2) = 4 + 0,12х2;
2) -0,125х(8х2 – 2) + х(х2 – 6,75) = 0;
3) 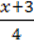 +
+ 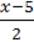 + 0,25(-x + 2) =
+ 0,25(-x + 2) = 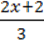 ;
;
4) 2×2 + x – 4 – 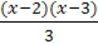 = -6;
= -6;
5) (0,1x –  )(0,6x +
)(0,6x +  ) – (5 + 3x)(
) – (5 + 3x)(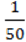 X – 0,4) = 0;
X – 0,4) = 0;
6) (1 X – 0,7)(
X – 0,7)( X – 1) –
X – 1) –  (x2 – x + 2,1) = 0.
(x2 – x + 2,1) = 0.
14. Доведіть, що сума многочленів – 0,125mn2 – 1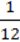 Mn – 1,27,
Mn – 1,27,  Mn2 + 1
Mn2 + 1 Mn – 1,23 і –
Mn – 1,23 і – mn + 4,5 дорівнює 2 не залежно відзначень змінних, що входять до нього.
mn + 4,5 дорівнює 2 не залежно відзначень змінних, що входять до нього.
15. Сума двох двоцифрових чисел, у яких однакове число десятків, дорівнює 90. Знайдіть ці числа, якщо число одиниць першого на 6 більше за число одиниць другого.
16. Двоцифрове число на 18 більше за суму його цифр. Знайдіть це число, якщо число одиниць на 2 менше від числа його десятків.
17. Обчисліть, не користуючись калькулятором:
1) 1112 – 111 – 42 + 212; 2) 8,672 + 3,672 – 3,67 ∙ 17,34;
3) 2462 + 5542 + 246 ∙ 1108; 4) 3,372 + 2,632 + 5,26 ∙ 3,37.
18. Подайте у вигляді многочлена вираз:
1) 5х(-3x + 4y)2; 2) 10аb(а – 0,1b)2;
3) 4x2y2 (3у2 – 2х2)2; 4) 5с2(2 + 0,4с)2.
19. Спростіть вираз:
1) (3 + 2b)2 – 24b; 3) (5 – а)2 – 5(5 – 2a);
2) (5 + 2с)2 – 4с2; 4) (4 + 3у)2 – (3у – 4)2.
20. Розв’яжіть рівняння:
1) (4х – 3)2 = 16х2; 3) (1 + 5х)2 – 5х(2 + 5х) = 0;
2) (3 +2x)2 = (2х – 1 )(2х – 5); 4) (7 + 4х)2 = 2х(8х + 3,5).
21. Доведіть тотожність: (х2 + у2)2 = (х2 – y2)2 + (2хy)2.
22. Задача Діофанта. Доведіть, що для будь-яких чисел a, b, с, d виконуються тотожності:
1) (а2 + b2)(с2 + d2) = (ac + bd)2 + (bc – ad)2;
2) (а2 + b2)(c2 + d2) = (aс – bd)2 + (bc + ad)2.
23. Спростіть вираз: (x2 + у – 4)2 – (x2 + у – 1 )(x2 + у – 8).
24. Знайдіть значення виразу: а2 +  , якщо:
, якщо:
1) а +  = 4,5; 2) а –
= 4,5; 2) а –  = 4,5.
= 4,5.
25. Обчисліть, не користуючись калькулятором:
1)982 – 482; 2) 2,322 – 0,682; 3)67 ∙ 73.
26. Вставте замість * одночлен так, щоб утворилась тотожність:
1) 9а2b2 – 81 = (* – 9)(* + 9);
2) (- m +7n)2 = * + 10mn + 49n2;
m +7n)2 = * + 10mn + 49n2;
3) (1 С – 6d)2= * – 12cd + 36d2;
С – 6d)2= * – 12cd + 36d2;
4) (0,6ab – 0,5x)2 = 0,36а2b2 – * + 0,25×2.
27. Розв’яжіть рівняння:
1) (11 + 5x)2 – (5x – 1)2 = 0; 3) (4x + 5)2 – (4x + 3)2= 0;
2) (3 + x)3 – x3 = 9×2; 4) (2 -3х)3= 9×2 ∙ (6 – 3x).
28. Доведіть, що за будь-якого натурального n значення виразу:
1) (3 + 2n)2 – (2 + 3n)2 ділиться на 5;
2) (4 + 2n)3 – 8n3 ділиться на 4
29. Спростіть вираз двома способами:
1) (х + 3)2 – (x – 3)2; 2)(х + 2)3 – (х – 2)3.
30. Доведіть, що:
1) різниця квадратів двох послідовних натуральних чисел є непарним числом;
2) різниця квадратів двох послідовних парних натуральних чисел ділиться на 4;
3) різниця квадратів двох послідовних непарних натуральних чисел ділиться на 8.
31. Площа квадрата дорівнює площі прямокутника, у якого одна сторона на 3 см менша від сторони квадрата, а інша – на 4 см більша за сторону квадрата. Знайдіть сторони квадрата і прямокутника.
32. Сторону квадрата зменшили на 3 см, при цьому його площа зменшилась на 39 см2. Знайдіть початкову сторону квадрата.
33. Сторону куба зменшили на 2 см, при цьому його об’єм зменшився на 218 см3. Знайдіть початкову сторону куба.
34. Розкладіть на множники многочлен:
1) 2b5 + 6а + 3b4 + 9; 3) х5у2 – 5х3 + 35 – 7х2у2;
2) (5х + 1 )3 – 64х3; 4) (-4а + 3ху)3 + 8х3у3.
35. Дано три послідовні натуральні числа. Доведіть, що добуток першого і третього числа дорівнює квадрату другого числа, зменшеного на 1.
Розділ 4. ФУНКЦІЇ
1. Дано функції: f(х) = -3х2 + 5х + 1 і g(x) = 2 + 2х2+ 3х.
Порівняйте: 1) f(1) і g(1); 2) f(2) і g( -2); 3) f(-1) і g(0).
2. Розв’яжіть рівняння f(x) = 0, якщо:
1) f(х) = 5х + 1; 2)f(х) = 5|х|-1; 3) f(х) = 5|х| + 1.
3. Розв’яжіть рівняння f(x) = g(2), якщо:
1) f(х) = 2х – 3, g(x) = 3х – 1;
2) f(x) = 2|x| + 1,g(x) = 5х – 7.
4. Знайдіть область визначення функції, заданої формулою:
1) y = –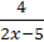 ;
;
2) y = x2 +  + 2;
+ 2;
3) y = 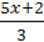 +
+ 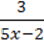 .
.
5. Знайдіть область значень функції, заданої формулою:
1)у = -5х2; 2)у = – х2 + 3; 3)у = 4х2 – 2;
6. Чи проходить через початок координат графік функції:
1) у = х2; 2) y = -6x + 1,4; 3) у =-3; 4) у = – Х?
Х?
7. Чи належить графіку функції у = -2х2 + 3х + 1 точка:
1)4 (-1; -4); 2) б (1; 0); 3) С (0; 1); 4) D (2; -1)?
8. Побудуйте графік функції:
1) у = 3х – 4; 3)у = -2х + 3;
2) y = 0,5x – 1,5; 4)у = |х-|.
9. Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції:
1) у = 3x – 11; 2) у = -3,5х + 14; 3) у = -2,4х + 3,6.
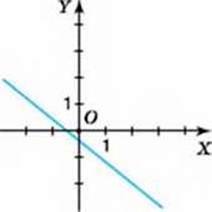
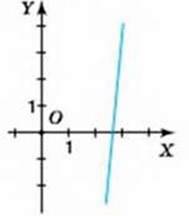
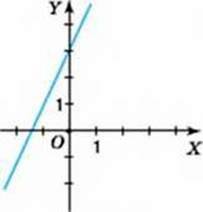
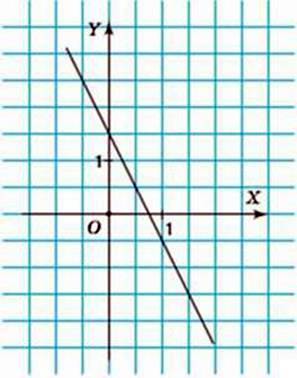
10. На малюнках 84-89 зображено графіки лінійних функцій, заданих формулою у = ах + b. Визначте знаки коефіцієнтів а і b.
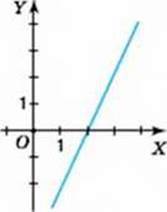
Мал. 84
Мал. 85
Мал. 86
Мал. 87
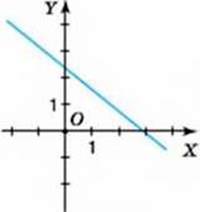
Мал. 88
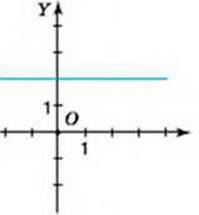
Мал. 89
11. Знайдіть координати точки графіка функції у = 4х +12, якщо:
1) абсциса і ордината точки рівні між собою;
2) абсциса і ордината точки є протилежними числами;
3) сума абсциси і ординати точки дорівнює 10.
12. Графік функції у = ах + и проходить через точки А (1; -3) і В (2; 2). Знайдіть значення a і b.
13. Графік функції y = kx + b проходить через точку А (1; 21), а його кутовий коефіцієнт дорівнює НСД чисел 168 і 360. Знайдіть значення k і b.
14. Задайте формулою функцію, графік якої є прямою, що паралельна осі ОХ і проходить через точку М (а; b). Накресліть у зошиті таблицю 38 та заповніть її.
Таблиця 38
М (а; b) | (3; -3) | (-1;_ ) | (- |
A | 2 | ||
B | 2 | 2,5 | |
Функція |
15. Чи належить графіку функції у = |2х – 1| – 2 точка:
1) A (1; -1); 2) B (1; 1); 3) C (-1; -5); 4) D (-1; 1)?
16. Знайдіть область значень функції:
1) y = |x| – 4; 2) у = |x| + 2; 3) у = 3|х|; 4) у = -5|х| + 1.
17. Побудуйте графік функції:
1) у = |х| – 2; 2) у = |x – 1| -2; 3) у = -|x| + 2; 4) у = |x + 1| +2.
18. Побудуйте графік функції:
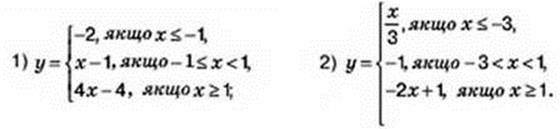
19. Побудуйте графік функції:
1) у = 2 | х | – 1;
2) y = -2| х – 1| – 1;
3) у =  |x| – 1;
|x| – 1;
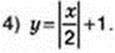
20. Побудуйте графік функції:
1) у = |х + 1| + |х – 2|; 2) у = | х -3| – |х + 1|.
21. На малюнках 90-91 зображено графіки лінійних функцій. Задайте формулами ці функції.
Мал. 90
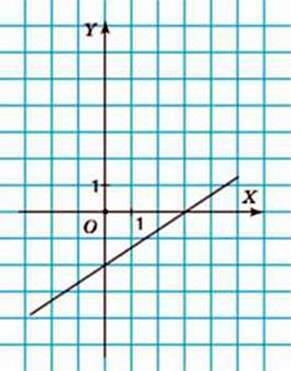
Мал. 91
22. Задайте формулою функцію, яка є прямою пропорційністю, а її графік проходить через точку N (a; b). Накресліть у зошиті таблицю 39 та заповніть її.
Таблиця 39
N (a, b) | (__; -8) | (-1;__) | (- |
А | -2 | 4 | |
B | 1 | -3,5 | |
Функція |
23. Побудуйте графік функції:
1) у = х; 2) у = -3х; 3) у = 0,25х.
24. Знайдіть область визначення і область значень функції:
1) y =  X: 3 )у = –
X: 3 )у = –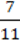 Х;
Х;
2) y = 2|х|; 4) y =  |x| .
|x| .
25. Побудуйте графік функції:
2) y = -3|x|;
3) y = -|2x| + x.
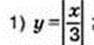
26. На малюнках 92-94 зображено графіки лінійних функцій, заданих формулою у = ах. Визначте знак коефіцієнта а.
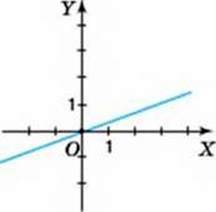
Мал. 92
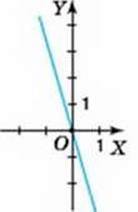
Мал. 93
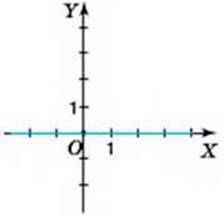
Мал. 94
27. Задайте формулою функцію, яка є прямою пропорційністю, якщо її графік проходить через точку, ордината якої в 5 раз менша від відповідної абсциси. Побудуйте графік отриманої функції.
28. Задайте формулою функцію, яка є прямою пропорційністю, якщо її графік проходить через точку, абсциса якої в 2,5 рази більша за відповідну ординату. Побудуйте графік отриманої функції.
29. Задайте формулою функцію, яка є прямою пропорційністю, якщо її кутовий коефіцієнт дорівнює середньому арифметичному всіх непарних додатних одноцифрових чисел. Побудуйте графік отриманої функції.
30. Задайте формулою функцію, яка є прямою пропорційністю, якщо її кутовий коефіцієнт є числом, протилежним до  від суми всіх двоцифрових чисел, кратних 7 і менших від 31. Побудуйте графік отриманої функції.
від суми всіх двоцифрових чисел, кратних 7 і менших від 31. Побудуйте графік отриманої функції.
Розділ 5. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
1. Чи є рівносильними рівняння:
1) 5х – 7 = 2х + 9 і 5х – 2х = 9 + 7;
2) 7 – 2у = 6у – 18 і 2у -6y = -18 – 7?
2. Знайдіть корінь рівняння:
1) 7 – 3х – 3 = 10 – 4х; 3) -1,2х + 5 = 3 – 0,4х;
2) 5 + 2у – 6 = 5у + 8; 4) 1,5у – 4 = 5 + 0,9у.
3. Розв’яжіть рівняння:
1) 2(х – 5,5) + 3 = 7,5 – 3,5(2х – 1);
2) 8 – 1,5(3х + 2) =  (4 – 6х);
(4 – 6х);
3) 0,8(3 – 10y) = 12 – 2,5(3y – 5);
4) 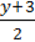 – 2y = – y – (1 –
– 2y = – y – (1 – 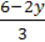 ).
).
4. Доведіть, що:
1) рівняння (х + 3)(х – 2) – (3 + х)2 = 9 має один корінь;
2) рівняння 5у(у + 2) = (2у + 1)2 + у2 + 6у немає коренів.
5. У двох 7-х класах навчаються 55 учнів, причому в 7-А класі на З учні більше, ніж у 7-Б класі. Скільки учнів навчається в кожному класі?
6. У трьох кошиках 120 яблук. У другому кошику на 20 яблук менше, ніж у першому, і на 15 яблук більше, ніж у третьому. Скільки яблук у кожному кошику?
7. Одна сторона прямокутника утричі більша за іншу. Знайдіть сторони прямокутника, якщо його периметр дорівнює 24 см.
8. Відстань між пунктами А і В дорівнює 390 км. Два автобуси одночасно виїхали із цих пунктів назустріч один одному і зустрілись через 3 години. Знайдіть швидкість кожного автобуса, якщо швидкість одного з них на 5 км/год менша від швидкості другого.
9. Знайдіть три послідовні натуральні числа, якщо їх сума дорівнює 906.
10. Для даного рівняння заповніть таблицю 40.
Таблиця 40
Лінійне рівняння із двома змінними | Х – у + 7 = 0 | 2х + у – 6 = 0 | Х – 2у + 10 = 0 |
Виразити у через х | |||
Виразити х через у |
11. У рівнянні 4х – 2у + 5 = 0 виразіть змінну:
1) у через змінну х;
2) х через змінну у.
Знайдіть два будь-яких розв’язки цього рівняння.
12. Побудуйте графік рівняння:
1) 2х – у + 3 = 0; 3) -3х – y + 4 = 0;
2) 5х – 2у = 0; 4) – х + 2у – 8 = 0.
1 3. До рівняння 2х – у + 3 = 0 доберіть друге рівняння так, щоб отримана система двох лінійних рівнянь із двома змінними: 1) мала один розв’язок; 2) не мала розв’язків; 3) мала безліч розв’язків.
14. Розв’яжіть графічно систему двох лінійних рівнянь із двома змінними:

15. Розв’яжіть систему рівнянь:

16. Розв’яжіть систему рівнянь:
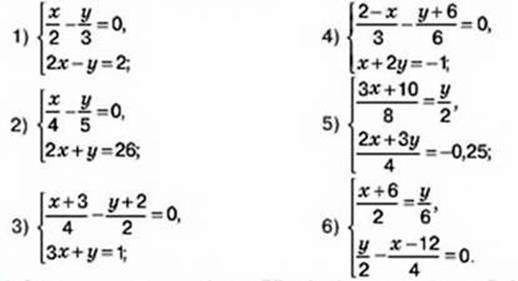
17. Сума двох чисел дорівнює 55, а їх різниця дорівнює 5. Знайдіть ці числа.
18. Сума двох чисел дорівнює 100. Знайдіть ці числа, якщо одне з них на 10 більше за інше.
19. Різниця двох чисел дорівнює 15. Знайдіть ці числа, якщо одне з них у 4 рази більше за друге.
20. Сума двох чисел дорівнює 33. Якщо від подвоєного першого числа відняти друге число, то отримаємо 12. Знайдіть ці числа.
21. Різниця двох чисел дорівнює 7. Якщо до першого числа додати подвоєне друге число, то отримаємо 31. Знайдіть ці числа.
22. Дано два числа. Сума подвоєного першого числа і другого числа дорівнює 17. Сума подвоєного другого числа і першого числа дорівнює 19. Знайдіть ці числа.
23. Дано два числа. Сума цих чисел дорівнює 80. Якщо одне із цих чисел зменшити у 2 рази, а друге число збільшити у 2 рази, то в сумі отримаємо число 115. Знайдіть ці числа.
24. Знайдіть дріб, який набуває значення  , якщо чисельник збільшити на 6, і набуває значення
, якщо чисельник збільшити на 6, і набуває значення  , якщо знаменник зменшити на 2.
, якщо знаменник зменшити на 2.
25. Якщо чисельник дробу помножити на 2, а від знаменника відняти 2, то отримаємо 2. Якщо ж від чисельника відняти 4, а знаменник помножити на 4, то отримаємо  . Знайдіть цей дріб.
. Знайдіть цей дріб.
26. За 5 кг печива і 3 кг цукерок заплатили 135 грн. Скільки коштує 1 кг печива, якщо він дешевший за 1 кг цукерок на 13 грн?
27. Легковий автомобіль за 3,5 години проїхав ту ж відстань, що і вантажний за 5 годин. Знайдіть їх швидкості, якщо швидкість легкового автомобіля на 30 км/год більша за швидкість вантажного автомобіля.
28. Два автомобілі виїхали одночасно з двох міст, відстань між якими 225 км, і зустрілися через 1,5 год. З якою швидкістю їхав кожний автомобіль, якщо перший проїхав до зустрічі на 15 км більше, ніж другий?
29. Із пункту А до пункту В виїхав легковий автомобіль зі швидкістю 90 км/год. У цей самий час вантажний автомобіль, що рухається в тому ж напрямку зі швидкістю 70 км/год, вже проїхав 100 км шляху. До пункту В автомобілі прибули одночасно. Знайдіть відстань між пунктами А і В.
30. Катер пропливає відстань між двома містами за 4 години за течією і за 6 годин проти течії. Знайдіть швидкість катера і течія річки, якщо відстань між селами дорівнює 60 км.
31. За 2 год за течією річки і 1 год проти течії моторний човен проходить 63 км, а за 1 год за течією і 2 год проти течії – 57 км. Знайдіть власну швидкість човна і швидкість течії річки.
32. Батько старший за доньку на 26 років, а через 4 роки він буде старший за неї утричі. Скільки років батьку і скільки років доньці?

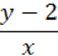

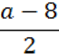

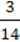 ;
;