Головна ⇒ 📌Математика ⇒ Задачі та приклади на всі дії з натуральними числами і десятковими дробами

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ

§ 45. Задачі та приклади на всі дії з натуральними числами і десятковими дробами

Початковий рівень

1620. Знайди (усно):

1) 1,8 + 3,1; 2) 0,05 + 0,18; 3) 4,2 – 1,2;

4) 100 ∙ 0,15; 5) 57 ∙ 0,1; 6) 0,73 : 0,1.

1621. Знайди (усно):

1) 7,8 + 4,9; 2) 3,7 + 2,51; 3) 1 – 0,6;

4) 2 – 0,17; 5) 0,001 ∙ 29; 6) 4,2 : 0,7.

1622. Обчисли (усно):

1) 0,57 + 1,43; 2) 4,27 – 2,07; 3) 4,1 – 2,01;

4) 8 ∙ 1,5; 5) 60 : 0,2; 6) 739 : 100.

1623. Обчисли (усно):

1) 8,32 ∙ 10; 2) 117,3 ∙ 100; 3) 1,85 ∙ 1000;

4) 3,71 ∙ 0,1; 5) 4,92 ∙ 0,01; 6) 125,3 ∙ 0,001.

1624. Обчисли (усно):

1) 32,7 : 10; 2) 45,13 : 100; 3) 2792 : 1000;

4) 8,3 : 0,1; 5) 37,3 : 0,01;

6) 13,24 : 0,001.

1625. Обчисли:

1) 5,18 + 25,37; 2) 0,805 + 7,105;

3) 5,97 + 0,032; 4) 8,91 – 1,328;

5) 71,5 – 16,07; 6) 42 – 7,18.

1626. Обчисли:

1) 4,27 + 37,42; 2) 0,913 + 8,39;

3) 4,13 + 0,9027; 4) 4,17 – 0,127;

5) 42,7 – 17,08; 6) 78 – 14,53.

1627. Обчисли:

1) 42 ∙ 0,13; 2) 3,6 ∙ 2,5; 3) 7,05 ∙ 800;

4) 15 : 4; 5) 72 : 2,25; 6) 15,3 : 17.

1628. Обчисли:

1) 38 ∙ 0,25; 2) 4,8 ∙ 3,5; 3) 4,07 ∙ 900;

4) 18,3 : 2; 5) 53,55 : 4,25; 6) 406,6 : 19.

1629. Запиши у вигляді десяткового дробу:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

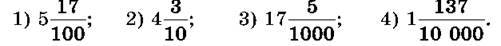
1630. Запиши у вигляді звичайного дробу або мішаного числа:

1) 2,3; 2) 4,07; 3) 0,23; 4) 10,073.

1631. Порівняй:

1) 4,897 і 4,879; 2) 7,520 і 7,52;

3) 42,57 і 42,572; 4) 9,759 і 9,758.

1632. Порівняй:

1) 7,896 і 7,869; 2) 8,01 і 8,1;

3) 47,53 і 47,530; 4) 4,571

і 4,578.

Середній рівень

1633. Обчисли 2,5x + 0,37, якщо:

1) x = 1,6; 2) x = 3,4.

1634. Знайди середнє арифметичне чисел:

1) 0,573; 1,96; 35,24;

2) 4,82; 89,59; 0,462; 9,368.

1635. Знайди середнє арифметичне чисел 20,76; 80,43; 90,24.

1636. За 2,5 год потяг проїхав 195 км. Скільки кілометрів проїде потяг за 3,6 год, якщо рухатиметься з тією самою швидкістю?

1637. Автомобіль протягом t годин їхав зі швидкістю 85 км/год. Склади вираз для знаходження шляху, пройденого автомобілем, і обчисли його, якщо t дорівнює 0,5; 0,8; 1,4; 3.

1638. Обчисли значення виразу 27,3 – а : b, якщо:

1) а = 33,5; b = 2,5; 2) а = 32,16; b = 13,4.

1639. Розв’яжи рівняння:

1) 12,5 + х = 37,4; 2) у + 13,72 = 18,1;

3) у – 137,8 = 27,41; 4) 17 – х = 12,42.

1640. Розв’яжи рівняння:

1) 13,7 + a = 18,4; 2) x + 13,42 = 18,9;

3) b – 142,3 = 15,73; 4) 14 – y = 12,142.

1641. Порівняй величини:

1) 0,4 м і 4 дм; 2) 0,2 дм і 20 см;

3) 0,07 м і 7 см; 4) 0,03 км і 300 м.

1642. Порівняй величини:

1) 0,2 т і 2 ц; 2) 0,3 ц і 31 кг;

3) 0,8 т і 785 кг; 4) 0,08 кг і 80 г.

1643. Швидкість теплохода у стоячій воді дорівнює 25,4 км/год, а швидкість течії річки – 1,8 км/год. Скільки кілометрів проходить теплохід:

1) за 1,5 год за течією річки;

2) за 2,4 год проти течії річки?

1644. Катер рухався спочатку 1,6 год озером зі швидкістю 25,5 км/год, а потім 0,8 год річкою проти течії. Швидкість течії дорівнює 1,7 км/год. Яку відстань подолав катер?

1645. Знайди значення виразу:

1) 15 ∙ (2,7 + 4,2);

2) (5,7 – 2,3) : 4;

3) (5,47 – 4,25) ∙ 10;

4) (4,47 + 2,7) : 10;

5) (13,42 – 4,15) ∙ (12,3 – 0,3);

6) (2,17 + 4,45) : (12,6 – 12,5).

1646. Знайди значення виразу:

1) (2,43 + 4,15) ∙ 1,7;

2) (12,49 – 3,57) : 0,4;

3) (4,17 – 3,8) ∙ (10,1 – 8,1);

4) (15,7 + 14,9) : (2,91 – 1,21).

1647. Розв’яжи рівняння:

1) 12,5х = 45; 2) у ∙ 4,8 = 60,6;

3) х : 4,7 = 12,3; 4) 12,7 : у = 0,01.

1648. Розв яжи рівняння:

1) 3,7y = 7,77; 2) х ∙ 3,48 = 8,7;

3) у : 5,4 = 13,5; 4) 52,54 : х = 3,7.

1649. Склади вираз: від суми чисел а і 42,3 відняти різницю чисел 15,7 і b. Обчисли значення виразу, якщо а = 3,7; b = 2,3.

1650. З 360 учнів школи 40 % брали участь у кросі. Скільки учнів брало участь у кросі?

1651. Знайди значення виразу:

1) (120,21 – 37,59) : 34 + 5,43 ∙ 19;

2) (8,57 + 9,585 : 4,5) ∙ 3,8 – 42,7 : 4.

1652. Знайди значення виразу:

1) (5,02 – 3,89) ∙ 29 + 0,27 : 18;

2) (32,526 : 3,9 + 2,26) ∙ 5,4 – 47,2 ∙ 0,5.

1653. На скільки сума чисел 19,4 і 4,72 більша за різницю цих самих чисел?

1654. Знайди суму 25,3 дм + 13,7 см + 15 мм у сантиметрах.

1655. 32 учні зібрали 152 кг полуниць і 33,6 кг малини. Скільки всього кілограмів ягід зібрав кожний учень, якщо вони зібрали ягід кожного виду порівну?

1656. З поля площею 420 га планувалося зібрати по 35 ц зерна з кожного гектара, але зібрали 1785 т зерна. На скільки центнерів урожай з 1 га вищий, ніж було заплановано?

1657. Знайди площу поверхні куба з ребром 1,5 см.

1658. Знайди площу та периметр квадрата зі стороною 4,7 дм.

1659. Запиши в порядку спадання дроби: 0,27; 0,372; 0,423; 0,279; 0,51; 0,431; 0,307.

1660. Запиши в порядку зростання дроби: 4,23; 4,32; 4,222; 43,2; 4,232; 4,323.

1661. Мотузку завдовжки 15,3 м розрізали на три частини. Одна з них становить 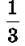Задачі та приклади на всі дії з натуральними числами і десятковими дробами мотузки, друга

Довша за першу на 1,8 м. Знайди довжину кожної частини.

1662. Яхта “Біда” за 3 дні регати подолала 234,9 км. За перший день яхта подолала Задачі та приклади на всі дії з натуральними числами і десятковими дробами цієї відстані, а за другий – на 8,3 км менше, ніж за перший. Скільки кілометрів яхта “Біда” долала кожного дня?

1663. Автомобіль проїхав 471 км. Перші 205 км він їхав зі швидкістю 82 км/год, а решту – зі швидкістю 76 км/год. За який час автомобіль подолав весь шлях?

1664. Периметр рівнобедреного трикутника дорівнює 15,4 см. Знайди його основу, якщо бічна сторона трикутника дорівнює 5,3 см.

1665. Знайди периметр рівнобедреного трикутника, основа якого дорівнює 4,2 дм, а бічна сторона в 1,5 раза більша за основу.

1666. Обчисли:

1) (88,57 + 66,87) : 29 – 0,27 ∙ 18;

2) 20,8 : (12 – 11,36) – 8 : 12,5 + 4,7 ∙ 5,2.

1667. Обчисли:

1) (1,37 + 4,86) ∙ 17 – 556,89 : 19;

2) (3,81 + 59,427 : 9,3) ∙ 7,6 – 10,2 ∙ 4,7.

1668. На скільки сума чисел 8,1 і 7,2 більша за їхню частку?

1669. На скільки різниця чисел 3,7 і 2,5 менша від їхнього добутку?

1670. Знайди значення виразу а ∙ 2,5 – b, якщо а = 3,6; b = 1,117.

1671. Між якими сусідніми натуральними числами розміщено дріб:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

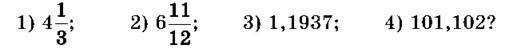
1672. Округли до:

1) одиниць: 25,17; 37,89;

2) десятих: 37,893; 42,012;

3) сотих: 108,112; 213,995.

1673. Округли до:

1) одиниць: 25,372; 37,51;

2) десятих: 13,185; 14,002;

3) сотих: 15,894; 17,377.

1674. Накресли координатний промінь, взявши за одиничний відрізок 10 клітинок. Познач на ньому точки А(0,7), B(1,3), С(1), D(0,2), D(1,9).

1675. Накресли координатний промінь, взявши за одиничний відрізок 10 клітинок. Познач на ньому точки М(0,6), N(1,4), K(0,3), L(2), Р(1,8).

1676. Білий ведмідь важить 720 кг, а маса бурого становить 40 % маси білого ведмедя. Обчисли масу бурого ведмедя.

1677. Спрости вираз 2,7x – 0,05x + 0,75x та знайди його значення, якщо х = 2,7.

1678. Основа рівнобедреного трикутника дорівнює 10,8 см, а довжина бічної сторони становить Задачі та приклади на всі дії з натуральними числами і десятковими дробами довжини основи. Знайди периметр трикутника.

1679. Спрости вираз та обчисли його значення:

1) 2,7а ∙ 2, якщо а = 3,5;

2) 3,2x ∙ 5у, якщо x = 0,1; у = 1,7.

1680. Знайди об’єм прямокутного паралелепіпеда, виміри якого дорівнюють:

1) 1,2 см, 5 см, 1,8 см; 2) 1,2 дм, 3 см, 23 мм.

1681. Вирази в тоннах і запиши у вигляді десяткового дробу:

1) 7314 кг; 2) 2 т 511 кг; 3) 3 ц 12 кг; 4) 18 кг.

1682. Вирази в метрах і запиши у вигляді десяткового дробу:

1) 527 см; 2) 12 дм; 3) 3 м 5 дм; 4) 5 м 4 см. 336

Достатній рівень

1683. Виконай ділення, одержану частку округли:

1) 110 : 57 до одиниць; 2) 18 : 7 до десятих;

3) 15,2 : 0,7 до сотих; 4) 14 : 5,1 до тисячних.

1684. Виконай ділення, одержану частку округли:

1) 120 : 37 до десятих; 2) 5,2 : 0,17 до сотих.

1685. Завод працював 15 днів і випускав щодня в середньому по 45,4 т мінеральних добрив. Усі добрива завантажили у 25 залізничних вагонів порівну. Скільки добрив завантажили в кожний вагон?

1686. Сума двох довжин трикутника дорівнює 15 см, а довжина третьої сторони становить 80 % цієї суми. Знайди периметр трикутника.

1687. Одна зі сторін прямокутника дорівнює 14,4 см, а довжина другої становить 75 % першої. Знайди площу та периметр цього прямокутника.

1688. Периметр трикутника дорівнює 36 см. Довжина однієї зі сторін становить Задачі та приклади на всі дії з натуральними числами і десятковими дробами периметра, а довжина другої – 40 % периметра. Знайди сторони трикутника.

1689. Довжина прямокутного паралелепіпеда дорівнює 16 дм, ширина становить 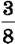Задачі та приклади на всі дії з натуральними числами і десятковими дробами довжини, а висота – 70 % ширини. Знайди об’єм прямокутного паралелепіпеда.

1690. Знайди суму трьох чисел, перше з яких дорівнює 4,27, а кожне наступне в 10 разів більше за попереднє.

1691. Висота прямокутного паралелепіпеда дорівнює 16 см, що становить 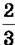Задачі та приклади на всі дії з натуральними числами і десятковими дробами довжини і 40 % ширини. Знайди об’єм прямокутного паралелепіпеда.

1692. Одна сторона прямокутника дорівнює 8,5 см, а друга становить 60 % першої. Знайди периметр та площу прямокутника.

1693. Один з робітників виготовив 96 деталей за 6 год, а інший – 45 деталей за 2,5 год. За скільки годин вони виготовлять 119 деталей, працюючи разом?

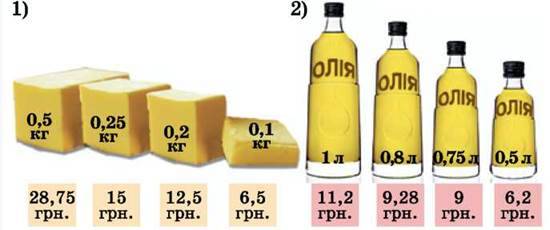
1694. Що вигідніше купити?

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

1695. Що вигідніше купити?

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

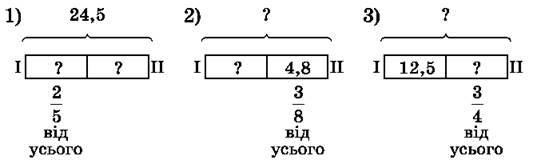
1696. Склади задачі за схемами і розв’яжи їх.

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

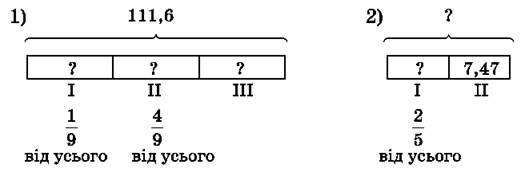
1697. Склади задачі за схемами і розв’яжи їх.

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

1698. На скільки збільшиться об’єм куба, якщо його ребро збільшити з 2,5 см до 3,5 см?

1699. Склади числовий вираз і знайди його значення:

1) різниця сум чисел 2,72 і 3,82 та 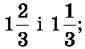Задачі та приклади на всі дії з натуральними числами і десятковими дробами

2) добуток різниці чисел 18,93 і 9,83 та числа 10.

1700. Із селища А в селище В одночасно виїхали два велосипедисти зі швидкостями 15,6 км/год та 18,4 км/год. Через 3,5 год один з велосипедистів прибув до селища В. Скільки ще кілометрів має проїхати інший велосипедист?

1701. З одного міста одночасно в протилежних напрямах виїхали два автомобілі. Швидкість одного з них – 76 км/год, що становить 95 % швидкості іншого. Через скільки годин відстань між автомобілями буде 390 км?

1702. Розв’яжи рівняння:

1) 1,17x + 0,32x = 3,725;

2) 4,7x – 1,2x = 4,34;

3) 2,47x – 1,32x + 1,3 = 4,221;

4) 1,4x + 2,7x – 8,113 = 2,342.

1703. Розв’яжи рівняння:

1) 4,13x – 0,17x = 9,9;

2) 5,3x + 4,8x – 5,13 = 43,35.

1704. Розгорнутий кут розділили променями на трикути. Перший становить 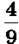Задачі та приклади на всі дії з натуральними числами і десятковими дробами розгорнутого, а другий –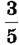Задачі та приклади на всі дії з натуральними числами і десятковими дробами першого. Знайди градусні міри трьох утворених кутів.

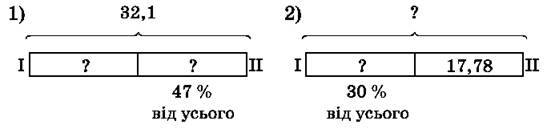
1705. Склади задачі за схемами та розв’яжи їх:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

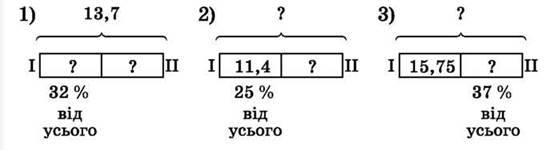
1706. Склади задачі за схемами та розв’яжи їх:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

1707. Розв’яжи рівняння:

1) 2,7(x – 4,7) = 9,45; 2) (4,7 + x) : 3,8 = 10,5;

3) 2,4 + (x : 3 – 5) = 0,8; 4) 2,45 : (2x – 1,4) = 3,5.

1708. Розв’яжи рівняння:

1) 21 : (4x + 1,6) = 2,5;

2) 3,7 – (x : 2 + 1,5) = 0,8.

1709. З 2,5 м мідного дроту, маса 1 м якого 1,2 кг, та шматка латунного дроту, довжина якого у 8 разів більша за мідний, а маса 1 м становить 0,2 кг, виготовили кулю. Скільки сплаву залишиться, якщо маса кулі 6,4 кг?

1710. Купили 2,5 кг печива за ціною 13,6 грн. за кілограм та цукерок 1,6 кг, ціна яких за один кілограм у 1,5 раза більша за ціну одного кілограма печива. Яку здачу мають отримати зі 100 грн.?

1711. Заповни клітинки цифрами, щоб утворилися правильні приклади:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

1712. Заповни клітинки такими цифрами, щоб утворилися правильні приклади:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

1713. Число 5,2 є середнім арифметичним чисел 2,1; 3,2 і х. Знайди х.

1714. Знайди середнє арифметичне чотирьох чисел, перше з яких дорівнює 3,6, а кожне наступне на 0,2 більше за попереднє.

1715. З одного міста в інше в одному напрямі одночасно вирушило двоє мотоциклістів зі швидкостями 72,4 км/год і 67,8 км/год. Через який час відстань між мотоциклістами буде 11,5 км?

1716. Ціна деякого товару 120 грн. Скільки коштуватиме цей товар, якщо ціну:

1) збільшити на 15 %;

2) зменшити на 10 %;

3) спочатку збільшити на 5 %, а потім нову ціну зменшити на 20 %?

1717. Знайди числа, яких не вистачає в ланцюжку обчислень:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

1718. Автомобіль проїхав за перші дві години 170,4 км, а за наступну – 0,45 цієї відстані. Знайди середню швидкість автомобіля.

1719. Потяг проїхав за перші три години 210,5 км, а за наступні дві – 0,6 цієї відстані. Знайди середню швидкість потяга.

1720. Сторона рівностороннього трикутника дорівнює 11,2 см. Знайди сторону квадрата, периметр якого дорівнює периметру трикутника. Визнач площу цього квадрата.

1721. Знайди заштриховану частину круга:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

1722. Знайди суму трьох чисел, перше з яких дорівнює 37,6, друге становить 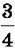Задачі та приклади на всі дії з натуральними числами і десятковими дробами першого, а третє є середнім арифметичним перших двох.

1723. Човен пройшов за 6 год проти течії річки 231 км. Який шлях він пройде за течією річки за 4 год, якщо швидкість течії становить 1,4 км/год?

1724. З двох пунктів, відстань між якими 8,5 км, у протилежних напрямах, віддаляючись один від одного, одночасно вийшло двоє пішоходів. Швидкість одного з них 4,2 км/год, що становить 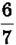Задачі та приклади на всі дії з натуральними числами і десятковими дробами швидкості другого. Яка відстань буде між пішоходами через 2,5 год?

1725. Автомобіль рухався 4 год зі швидкістю 82,5 км/год і 6 год зі швидкістю 83,7 км/год. Знайди середню швидкість автомобіля на всьому шляху.

Високий рівень

1726. Карлсон і Малюк разом з’їли 3,6 кг варення, причому Карлсон з’їв у 3 рази більше, ніж Малюк. Скільки варення з’їв Карлсон і скільки Малюк?

1727. Вантаж масою 4,8 т розмістили на двох вантажних автомобілях, причому на перший навантажили на 0,6 т більше, ніж на другий. Скільки тонн вантажу на кожному автомобілі?

1728. Робітники, працюючи втрьох, за 7 год виготовили 1001 деталь. Причому перший виготовив 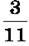Задачі та приклади на всі дії з натуральними числами і десятковими дробами усіх деталей, а другий – 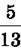Задачі та приклади на всі дії з натуральними числами і десятковими дробами усіх деталей. Скільки деталей за годину виготовляв третій робітник?

1729. Від деякого числа відняли його 10 % і отримали 48,6. Знайди це число.

1730. До деякого числа додали його 20 % і отримали 74,4. Знайди це число.

1731. Знайди два числа, якщо їхня сума 4,7, а різниця 3,1.

1732. Сума двох чисел дорівнює 27,2. Знайди ці числа, якщо одне з них утричі більше за інше.

1733. Мотузку завдовжки 10,6 м розрізали на три частини. Знайди їхні довжини, якщо третя частина на 0,4 м більша як за першу, так і за другу.

1734. Власна швидкість катера в 13 разів більша за швидкість течії. Рухаючись за течією 2,5 год, катер подолав 63 км. Знайди власну швидкість катера і швидкість течії.

1735. З двох станцій, відстань між якими дорівнює 385 км, вирушили одночасно назустріч один одному два потяги і зустрілися через 2,5 год. Знайди швидкості потягів, якщо відомо, що швидкість одного з них у 1,2 раза більша за швидкість іншого.

1736. Сума довжини і ширини прямокутника дорівнює 9,6 см, причому ширина становить 60 % довжини. Знайди площу і периметр прямокутника.

1737. Довжина однієї сторони трикутника становить 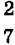Задачі та приклади на всі дії з натуральними числами і десятковими дробами периметра, а довжина іншої сторони – 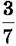Задачі та приклади на всі дії з натуральними числами і десятковими дробами периметра. Знайди довжини цих сторін, якщо третя сторона дорівнює 10,4 см.

1738. Учень прочитав спочатку 0,25 усієї книжки, а потім ще 0,4 решти, після чого виявилося, що учень прочитав на 30 сторінок більше, ніж йому залишилося прочитати. Скільки сторінок у книжці?

1739. Знайди значення букв g, h, m, n, k, l, якщо:

G : n = 1,8; n ∙ k = 1,71; h + m = 2,13;

K + l = 10,44; m ∙ 0,9 = 1,17; g – h = 0,79.

1740. IS У трьох ящиках разом 62,88 кг товару. У першому ящику товару в 1,4 раза більше, ніж у другому, а в третьому – стільки товару, скільки його в першому та другому разом. Скільки кілограмів товару в кожному ящику?

Вправи для повторення

1741. 1) Виконай дії:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

2) Виконай дії:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

3) Порівняй числа, позначені фігурами:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

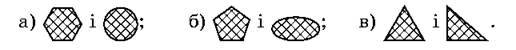
1742. 1) Виконай дії:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

2) Виконай дії:

Задачі та приклади на всі дії з натуральними числами і десятковими дробами

2. Знайди середнє арифметичне чисел 1,8 і 2,6.

А) 1,8; Б) 2; В) 2,6; Г) 2,2.

3. Запиши у вигляді десяткового дробу мішане число 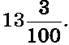Задачі та приклади на всі дії з натуральними числами і десятковими дробами

А) 3,13; Б) 13,3; В) 13,003; Г) 13,03.

4. Після перегонки нафти отримують 30 % гасу. Скільки гасу отримують з 18 т нафти?

А) 6 т; Б) 5,4 т; В) 54 т; Г) 0,6 т.

5. З молока виходить 9 % сиру. Скільки було взято молока, якщо сиру отримали 36 кг?

А) 400 кг; Б) 40 кг; В) 324 кг; Г) 300 кг.

6. У команді баскетболістів двом гравцям по 19 років, двом – по 21 року, а одному гравцеві – 26 років. Який середній вік гравців цієї команди?

A) 19 років; Б) 21 рік;

B) 21,2 року; Г) 21,4 року.

7. Під час сушіння гриби втрачають 89 % своєї маси. Скільки сухих грибів одержимо з 60 кг свіжих?

А) 53,4 кг; Б) 6,6 кг; В) 6 кг; Г) 5,34 кг.

8. Коли учень прочитав 30 % книжки, то помітив, що йому залишилося прочитати ще 105 сторінок. Скільки сторінок у книзі?

А) 350 с.; Б) 250 с.; В) 150 с.; Г) 160 с.

9. Один з операторів комп’ютерного набору набрав 45 сторінок тексту за 6 годин, а інший – 26 сторінок тексту за 4 години. За скільки годин, працюючи разом, вони наберуть 35 сторінок?

А) 2 год; Б) 2,5 год; В) 3 год; Г) 3,5 год.

10. У шухляді знаходяться білі і чорні кульки, причому білі становлять 30 % усіх кульок. Скільки в шухляді кульок усього, якщо чорних кульок на 32 більше, ніж білих?

А) 80; Б) 70; В) 56; Г) 180.

11. Середнє арифметичне двох чисел, одне з яких у 4 рази більше за інше, дорівнює 6. Знайдіть менше з цих двох чисел.

А) 1,5; Б) 2,4; В) 2,5; Г) 9,6.

12. Ціна деякого товару 150 грн. Скільки коштуватиме цей товар, якщо спочатку ціну товару збільшити на 10 %, а потім нову ціну зменшити на 15 %?

А) 142,5 грн.; Б) 157,5 грн.;

В) 155 грн.; Г) 140,25 грн.

Завдання для перевірки знань № 9 (§42 – §45)

1. Запиши у вигляді десяткового дробу:

1) 15 %; 2) 3 %.

2. Запиши у відсотках десятковий дріб:

1) 0,45; 2) 1,37.

3. Виконай дії:

1) 3,7 + 13,42; 2) 15,8 – 13,12;

3) 4,2 ∙ 2,05; 4) 8,64 : 2,4.

4. З 1200 учнів, що навчаються в школі, 65 % брали участь у спартакіаді. Скільки учнів брали участь у спартакіаді?

5. Сергій купив книжку за 8 грн., що становить 40 % грошей, які в нього були. Скільки гривень було в Сергія?

6. Знайди середнє арифметичне чисел 48,5; 58,2; 46,8; 42,2.

7. Робітник виготовив 320 деталей. За першу годину – 35 % усіх деталей, за другу – 40 %, а за третю – решту. Скільки деталей виготовив робітник за третю годину?

8. Автомобіль їхав 2 год зі швидкістю 66,7 км/год і 3 год зі швидкістю 72,8 км/год. Знайди його середню швидкість на всьому шляху.

9. Турист пройшов за три дні 56 км. За перший день він пройшов 30 % усього маршруту, що становить 80 % відстані, пройденої туристом за другий день. Скільки кілометрів пройшов турист за третій день?

10. Додаткове завдання. Довжина прямокутного паралелепіпеда дорівнює 8,5 см, що в 2,5 раза більше за ширину і на 5,1 см більше за висоту. Знайди об’єм цього прямокутного паралелепіпеда.

11. Додаткове завдання. Середнє арифметичне двох чисел дорівнює 12,4, а середнє арифметичне восьми інших чисел – 10,7. Знайди середнє арифметичне цих десяти чисел.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Приклади та задачі на всі дії з натуральними числами Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 15. Приклади та задачі на всі дії з натуральними числами Обчислюючи значення числових виразів, слід не забувати про порядок дій. Порядок виконання дій визначається такими правилами: 1. У виразах із дужками спочатку обчислюються значення виразів у дужках. 2. У виразах без дужок […]...

  2. Розв’язування вправ на всі дії зі звичайними та десятковими дробами Розділ 2 Звичайні дроби §19. Розв’язування вправ на всі дії зі звичайними та десятковими дробами 460. (Усно) Збільши на кожне із чисел: 461. (Усно) Зменши на кожне із чисел: 462. Запиши звичайним нескоротним дробом: 1) 0,13; 2) 0,2; 3) 1,5; 4) 1 %; 5) 7 %; 6) 40 %. 463. (Усно) Збільши у 2 рази […]...

  3. ДІЇ ДРУГОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ ЗАДАЧІ НА ПОВТОРЕННЯ ДІЇ ДРУГОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ 31. Виконайте множення: 1)325∙2802; 3)30865∙2010; 2) 407 ∙ 12025; 4) 72343 ∙ 4560180. 32. Обчисліть зручним способом: 1)382∙2∙50; 3) 125 ∙ (72 ∙ 8); 5) 40 ∙ (496 ∙ 25); 2)25∙74∙4; 4) 5 ∙ (315 ∙ 20); 6) 12∙ (5 ∙11). 33. Спростіть вираз: 1)9∙а∙12∙5∙b; 4) […]...

  4. Дії з десятковими дробами – Десяткові дроби Математика – Алгебра Десяткові дроби Дії з десятковими дробами Додавання та віднімання Для додавання (віднімання) десяткових дробів необхідно: 1) зрівняти в дробах кількість знаків після ­коми; 2) записати дроби один під одним так, щоб кому було записано під комою; 3) виконати додавання (віднімання), не звертаючи уваги на кому; 4) у відповіді поставити кому під комами […]...

  5. Дії ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ ЗАДАЧІ НА ПОВТОРЕННЯ Дії ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ 14. Спростіть вираз: 1) а + 2 – а + 10 + b – b + 3; 2) 3а + b + 3 + b + 4а. 15. Знайдіть значення виразу 2а + 78, якщо: 1) а = 11; 2) а = 25. 16. Альбом коштує […]...

  6. Дії над натуральними числами Математика – Алгебра Натуральні числа і дії над ними Дії над натуральними числами Додавання У записі числа a і b – доданки, число с, а також вираз – сума чисел а і b. Властивості додавання 1. Переставна. Від перестановки доданків сума не змінюється: . 2. Сполучна. Щоб до суми двох чисел додати третє число, можна […]...

  7. ПОВТОРЕННЯ. ДІЇ ДРУГОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ Цілі: – навчальна: повторити поняття множення та ділення натуральних чисел, закони множення; відтворити вміння виконувати множення та ділення натуральних чисел, розв’язувати задачі, які передбачають множення та ділення натуральних чисел; – розливальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип уроку: узагальнення та систематизація знань. Обладнання та наочність: Хід […]...

  8. Розв’язування вправ на всі дії з раціональними числами Розділ 4 Раціональні числа і дії мідними §50. Розв’язування вправ на всі дії з раціональними числами 1414. (Усно) Обчисли: 1) 5 + (-3); 2) -3 + (-8); 3) 4 – 7; 4) -2 – (-4); 5) -5,3 ∙ (-10); 6) -4,2 ∙ 0,1; 7) 4,7 : (-10); 8) -8,3 : (-0,1). 1415. (Усно) Обчисли: 1) […]...

  9. ПОВТОРЕННЯ. ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ Цілі: – навчальна: повторити поняття суми та різниці чисел, закони додавання; відтворити вміння виконувати додавання та віднімання багатоцифрових чисел, розв’язувати задачі, які передбачають додавання та віднімання чисел; повторити означення многокутника та його периметра, класифікацію трикутників; – розливальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип уроку: узагальнення та […]...

  10. Дії з іменованими числами. Знаходження значень виразів на сумісні дії з багатоцифровими числами. Задачі на спільну роботу (№№ 1059-1066) Тема. Дії з іменованими числами. Знаходження значень виразів на сумісні дії з багатоцифровими числами. Задачі на спільну роботу (№№ 1059-1066). Мета. Вправляти учнів у знаходженні значень виразів на сумісні дії з багатоцифровими числами; удосконалювати вміння розв’язувати рівняння, задачі на спільну роботу. Обладнання. Схема задачі; картки для опитування. Зміст уроку I. Контроль, корекція і закріплення знань. […]...

  11. ЗАДАЧІ НА ВИЗНАЧЕННЯ ЧАСУ ЗА ВІДСТАННЮ І ШВИДКІСТЮ. ДІЇ З ІМЕНОВАНИМИ ЧИСЛАМИ Мета: ознайомити учнів зі способом визначення часу за відомими швидкістю і відстанню; вдосконалювати вміння додавати і віднімати іменовані числа; розвивати уважність; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення – Обчисліть способом округлення. 3. Математичний диктант – Запишіть тільки відповіді. – […]...

  12. Знаходження значень виразів на сумісні дії з багатоцифровими числами. Розширені задачі на зведення до одиниці. Складання і розв’язування нерівностей (№№ 1067-1075) Тема. Знаходження значень виразів на сумісні дії з багатоцифровими числами. Розширені задачі на зведення до одиниці. Складання і розв’язування нерівностей (№№ 1067 – 1075). Мета. Виправляти учнів у знаходженні значень виразів на сумісні дії з багатоцифровими числами; удосконалювати вміння розв’язувати задачі на зведення до одиниці; вчити складати і розв’язувати нерівності. Обладнання. Завдання для опитування учнів; […]...

  13. Складені задачі, які містять знаходження дробу від числа Складені задачі, які містять знаходження дробу від числа 1 Знайди: 1) від 98; від 95; від 51; від 64. 2) число, якщо його становлять 98; Число, якщо його становлять 95. 2 Знайди, скільки: Метрів у км, у км; кілограмів у ц, у т. 3 Знайди, записавши відповідні вирази. 1) числа b; числа 125; числа k; […]...

  14. Strong>Ознайомлення з дробами 5. Множення і ділення багатоцифрових чисел Ознайомлення з дробами Ти вже знаєш, що таке натуральні числа, вмієш їх порівнювати і виконувати над ними арифметичні дії. Прочитай пояснення про дробові числа, або дроби. Якщо ціле яблуко поділити на дві рівні частини і взяти одну таку частину, то вона називається половина. Половина від цілого називається одна друга […]...

  15. ПЛОЩА ПРЯМОКУТНИКА ПЛОЩА ПЛОЩА ПРЯМОКУТНИКА 627. Знайди площі трьох фігур. Перевір обчисленнями. Порівняй. 628. Прямокутник ABCD поділений на квадратні сантиметри. Полічи, скільки квадратних сантиметрів у прямокутнику. Знайди число квадратних сантиметрів: 1) додаванням: А) 5 см2 + 5 см2 + 5 см2 =15 см2. (в одному ряду 5 одиничних квадратів, а рядів три). Б) 3 см2 + 3 […]...

  16. Комбінаторні задачі – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Комбінаторні задачі Задача 1. Запишіть усі трицифрові числа, що складаються із цифр 3, 4, 7, причому в записі цих чисел кожна цифра має використовуватися один раз. Розв’язання І спосіб Першу цифру в числі можна обрати трьома способами, цифру, яка стоїть на другому місці,- двома способами; на третьому місці […]...

  17. ПРИКЛАДИ ТА ЗАДАЧІ НА ЗАСВОЄННЯ ТАБЛИЦЬ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 2-5. МНОГОКУТНИК ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ Урок 15. ПРИКЛАДИ ТА ЗАДАЧІ НА ЗАСВОЄННЯ ТАБЛИЦЬ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 2-5. МНОГОКУТНИК Мета: закріпити знання вивчених таблиць додавання і віднімання; розвивати вміння розв’язувати задачі; формувати вміння використовувати прийоми обчислень для розвитку навичок швидкої лічби; виховувати уважність. […]...

  18. Задачі на знаходження часу за швидкістю і відстанню. Дії над іменованими числами (№№ 510-519) Тема. Задачі на знаходження часу за швидкістю і відстанню. Дії над іменованими числами (№№ 510-519). Мета. Ознайомити учнів із способом визначення часу за відомими швидкістю і відстанню; повторити виконання дій над іменованими числами. Обладнання. Таблиця усних обчислень; картки для опитування; таблиці-схеми задач. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка домашнього завдання. А) […]...

  19. ЗАДАЧІ НА ОБЧИСЛЕННЯ ПЛОЩІ ПЛОЩА ЗАДАЧІ НА ОБЧИСЛЕННЯ ПЛОЩІ 668. Поясни, як складено таблицю одиниць площі. 1 км2 = 1 000 000 м2 1 а = 100 м2 1 м2 = 100 дм2 1 га = 10 000 м2 1м2 = 10 000 см2 1 га = 100 а 1 см2 =100 мм2 1 дм2 = 100 см2 669. […]...

  20. Задачі на рух – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Задачі на рух Задача. Відстань від А до В дорівнює 120 км. Відстань від А до В автомобіль проїхав зі швидкістю 40 км/год, а від В до А – зі швидкістю 60 км/год. Яка середня швидкість його руху? Розв’язання Щоб знайти середню швидкість автомобіля, треба весь шлях поділити […]...

  21. Прості і складені задачі на визначення швидкості, часу і відстані. Дії над іменованими числами. Ознайомлення з назвами геометричних тіл Повторення вивченого (№№ 520-530) Тема. Прості і складені задачі на визначення швидкості, часу і відстані. Дії над іменованими числами. Ознайомлення з назвами геометричних тіл Повторення вивченого (№№ 520-530). Мета. Узагальнити зв’язки між відстанню, часом і швидкістю; закріплювати вміння учнів розв’язувати задачі на обчислення згаданих величин, виконувати дії над іменованими числами; ознайомити з назвами геометричних тіл. Обладнання. Таблиця усних обчислень; […]...

  22. ЗАДАЧІ НА СПОСІБ ЗВЕДЕННЯ ДО ОДИНИЦІ (перший вид). ДІЇ З ІМЕНОВАНИМИ ЧИСЛАМИ Мета: формувати вміння учнів розв’язувати задачі на спосіб зведення до одиниці; закріпити знання табличних випадків множення і ділення; вдосконалювати вміння виконувати перетворення іменованих чисел; розвивати обчислювальні навички, мислення; виховувати старанність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Гра “Хто швидше?” Усні обчислення за завданням 199 (с. 30). 3. […]...

  23. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧАСУ ЗА ВІДСТАННЮ І ШВИДКІСТЮ. ДІЇ ЗІ СКЛАДЕНИМИ ІМЕНОВАНИМИ ЧИСЛАМИ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ОЗНАЙОМИТИ ЗІ ЗНАХОДЖЕННЯМ ЧАСУ ЗА ВІДОМИМИ ШВИДКІСТЮ І ВІДСТАННЮ; ЗАКРІПИТИ ВМІННЯ ВИКОНУВАТИ ДІЇ ЗІ СКЛАДЕНИМИ ІМЕНОВАНИМИ ЧИСЛАМИ I. Перевірка домашнього завдання Записати вираз до задачі 509. Значення виразів вправи 508 звірити з раніше записаними вчителем на дошці. II. Активізація та корекція опорних знань учнів 1. Завдання для опитування. Як знайти швидкість, якщо […]...

  24. ЧИТАННЯ І ЗАПИС П’ЯТИЦИФРОВИХ ЧИСЕЛ. ДІЇ НАД КРУГЛИМИ ЧИСЛАМИ. ЗАДАЧІ НА ЗНАХОДЖЕННЯ НЕВІДОМИХ ЗА ДВОМА РІЗНИЦЯМИ Мета: формувати в учнів уміння читати і записувати п’ятицифрові числа; вчити застосовувати усні прийоми виконання дій над круглими п’ятицифровими числами; вдосконалювати обчислювальні навички, вміння розв’язувати задачі; розвивати мислення; виховувати уважність. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Математичний диктант – Запишіть числа цифрами: двадцять чотири тисячі […]...

  25. ШВИДКІСТЬ. ПРИКЛАДИ ШВИДКОСТЕЙ ШВИДКІСТЬ ШВИДКІСТЬ. ПРИКЛАДИ ШВИДКОСТЕЙ 740. Запиши об’єкти від най повільнішого до найшвидшого – Швидкість тіла це відстань, яку проходить тіло за одиницю часу. Наприклад. Швидкість літака 900 км за 1 год, велосипедиста 15 км за 1 год, черепахи – 7 м за 1 хв, людини 4 км за 1 год. Якою може бути швидкість автомобіля? […]...

  26. Правило знаходження шляху; часу руху Правило знаходження шляху; часу руху S = v. t T = s : v 1 Поясни, як ти розумієш: швидкість руху пароплава становить 5 000 м/год; потяга – 45 км/год; літака – 242 м/с; автомобіля – 90 км/год. 2 Визнач, із якою швидкістю рухається: вершник, якщо він щогодини проїжджає 9 км; поштовий голуб, якщо він […]...

  27. Задачі на пряму та обернену пропорційність – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Задачі на пряму та обернену пропорційність Задача 1. На пошиття 20 костюмів витратили 83 м тканини. Скільки таких самих костюмів вийде з 58,1 м тканини? Розв’язання Запишемо умову задачі у вигляді: Залежність між витраченою тканиною й кількістю костюмів – пряма пропорційність. (Тобто у скільки разів більше костюмів, у […]...

  28. Задачі з величинами: шлях, швидкість руху, час руху Задачі з величинами: шлях, швидкість руху, час руху 1 Обчисли. 2 Поясни, як ти розумієш: швидкість руху зебри дорівнює 25 м/хв; легкового автомобіля – 120 км/год. 3 Визнач, із якою швидкістю рухається ворона, якщо вона щосекунди пролітає 12 м. 4 Розв’яжи задачу. Склади та розв’яжи усно можливі обернені задачі. □ Підводний човен проплив 874 км […]...

  29. Складені задачі з величинами: шлях, швидкість руху, час руху Складені задачі з величинами: шлях, швидкість руху, час руху 1 Зістав задачі 1 і 2; 3 і 4. Що в них спільне? Що можна сказати про їх розв’язання? Розв’яжи задачі. □ 1) 78 кг картоплі розклали порівну у 3 великі сітки, а 26 кг – у 2 маленькі сітки. У скільки разів більше картоплі в […]...

  30. Арифметичні дії з круглими числами Арифметичні дії з круглими числами Спосіб укрупнення розрядних одиниць 1 У кожному з поданих чисел визнач загальну кількість одиниць кожного розряду. 36709 578023 301678 80045 101010 2 Які розрядні одиниці ти знаєш? Заміни круглі числа більшими розрядними одиницями. 56000 45800 160000 576890 500000 3 Знайди значення виразів способом укрупнення розрядних одиниць. 360 + 280 910 […]...

  31. ПИСЬМОВЕ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 3 КЛАС ПИСЬМОВЕ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 39. Розв’яжи задачу складанням виразу. У хорі Будинку творчості 85 дітей, у гуртку з моделювання на 39 дітей менше, ніж у хорі, а в танцювальних колективах на 19 дітей більше, ніж у хорі й гуртку з моделювання разом. Скільки дітей займаються в танцювальних колективах? 40. […]...

  32. Задачі на одночасний рух двох тіл у різних напрямках ст.50 Задачі на одночасний рух двох тіл у різних напрямках – Задачі на знаходження відстані; на знаходження швидкості руху – Два способи розв’язування задач 1 Розв’яжи задачі 1 і 2. Зістав їх. Чи допоможе тобі розв’язання задачі 1 розв’язати задачу 2 іншим способом? Поясни подане розв’язання задачі 2. 1) Мисливець і борсук опинилися біля куща, злякались […]...

  33. Задачі на дроби – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Задачі на дроби 1. Щоб знайти дроб від числа, треба це число поділити на знаменник і одержане число помножити на чисельник дробу. Задача. У бочці було 60 л води. Відлили усієї води. Скільки води залишилось? Розв’язання I спосіб: 1) (л) води відлили; 2) (л) залишилось. II спосіб: 1) […]...

  34. Задачі на процеси Задачі на процеси – Задачі на рух двох тіл у різних напрямках – Задачі на спільну роботу 1 За даними таблиці склади задачі на одночасний рух двох тіл у різних напрямках. Що цікаве можна помітити? Визнач, що має бути шуканим, щоб розв’язанням задачі був кожний вираз із поданих. V (км/год) T (год) S (км) І […]...

  35. Задачі на пропорційне ділення ст.10 Задачі на пропорційне ділення 1 Розв’яжи задачу 1. Зістав задачі 1 і 2. Як зміна вплине на розв’язання задачі 2? Розв’яжи її, скориставшись підказками. 1) Оля і Юля купили однакову кількість тістечок: Оля – за ціною 12 грн, а Юля – за ціною 13 грн. Скільки заплатила Юля, якщо Оля заплатила 60 грн? 2) Оля […]...

  36. Розв’язування задач на всі дії з дробами Урок № 3 7 Тема. Розв’язування задач на всі дії з дробами Мета: підготувати учнів до виконання тематичної контрольної роботи. Тип уроку: систематизація і корекція знань, умінь навичок. Хід уроку I. Перевірка домашнього завдання Самостійна робота із наступною перевіркою 1. Виконайте дії: а) ; б) ; в) ; г) . 2. Обчисліть значення виразу 8(4х […]...

  37. Сумісні дії з багатоцифровими числами. Розширені задачі на знаходження суми двох добутків. Складання та розв’язування рівнянь. Ділення іменованих чисел (№№ 1076-1084) Тема. Сумісні дії з багатоцифровими числами. Розширені задачі на знаходження суми двох добутків. Складання та розв’язування рівнянь. Ділення іменованих чисел (№№ 1076-1084). Мета. Закріплювати вміння учнів знаходити значення виразів на сумісні дії з багатоцифровими числами; удосконалювати вміння розв’язувати задачі на знаходження суми двох добутків; вчити складати та розв’язувати рівняння, ділити іменовані числа. Обладнання. Таблиця для […]...

  38. Задачі на пропорційне ділення ст.6 Задачі на пропорційне ділення Однакова величина – величина одиниці виміру 1 Обчисли. 2 Розв’яжи задачу 1. Зістав задачі 1 і 2. У чому відмінність? Як ця відмінність вплине на розв’язання задачі 2? 1) До обіду насос працював 4 год, а після обіду – 3 год. Скільки літрів води накачав насос до обіду та після обіду […]...

  39. Нумерація трицифрових чисел. Множення й ділення з числами 0 і 1. Задачі на знаходження суми двох добутків УРОК 2 Тема. Нумерація трицифрових чисел. Множення й ділення з числами 0 і 1. Задачі на знаходження суми двох добутків Мета: провести бесіду про значення числа 0 у записі числа; повторити множення й ділення з числами 1 і 0 та правила множення й ділення суми на число та ділення числа на добуток; розвивати в учнів […]...

  40. Ділення багатоцифрових чисел на одноцифрові. Ускладнені задачі на зведення до одиниці (№№ 655-662) Тема. Ділення багатоцифрових чисел на одноцифрові. Ускладнені задачі на зведення до одиниці (№№ 655-662). Мета. Закріплювати вміння учнів ділити багатоцифрові числа на одноцифрові; удосконалювати вміння розв’язувати задачі на зведення до одиниці; вправляти у ділені іменованих чисел. Таблиця. Таблиця усних обчислень; картки для опитування. Зміст уроку I. Контроль, корекція та закріплення знань. 1. Перевірка домашнього завдання. […]...

Ви зараз читаєте: Задачі та приклади на всі дії з натуральними числами і десятковими дробами
«
»