Запитання і вправи для повторення § 7
Відповідь: (3; 3), (-1; -2), (1; 0,5).
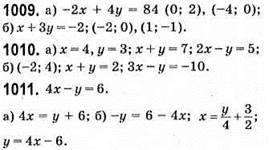
1012. а) х – 2y = 4;
X | 0 | 4 |
Y | -2 | 0 |
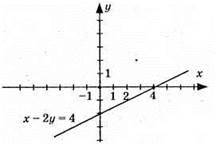
Б) 4х + у = -4;
X | 0 | -1 |
Y | -4 | 0 |
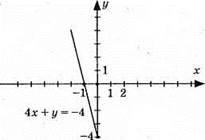
В) 3х – 2y = 6.
X | 0 | 2 |
У | -3 | 0 |
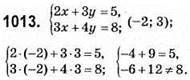
Відповідь: пара чисел (-2; 3) не являється розв’язком системи рівнянь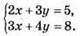 
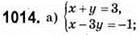
Х + y = 3;
X | 0 | 3 |
Y | 3 | 0 |
Х – 3у = -1;
X | 2 | -1 |
Y | 1 | 0 |
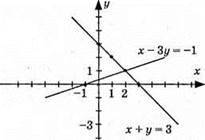
Відповідь: (2; 1).
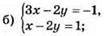
3х – 2у = -1,
X | 1 | -1 |
У | 2 | -1 |
Х
X | 1 | 3 |
У | 0 | 1 |
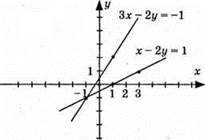
Відповідь: (-1; -1).
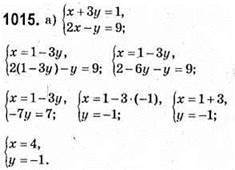
Відповідь: (4; -1).
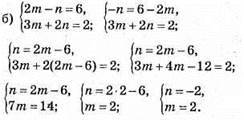
Відповідь: (2; -2).
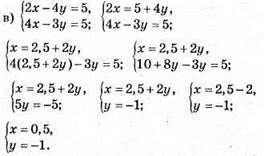
Відповідь: (0,5; -1).
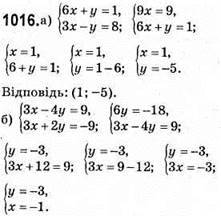
Відповідь: (-1; -3).
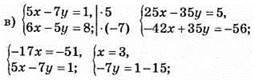
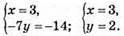
Відповідь: (3; 2).
1017. 2x – 3у = 1 і x + 3y = 5. Для того, щоб знайти координати точки перетину графіків рівнянь, потрібно розв’язати систему цих рівнянь:
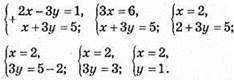
Відповідь: (2; 1).
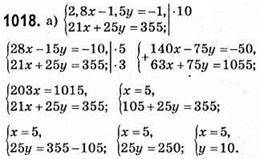
Відповідь: (5; 10).
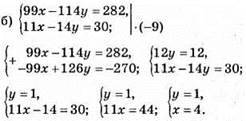
Відповідь: (4; 1).
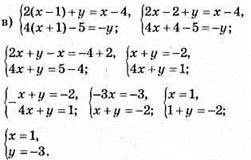
Відповідь: (1; -3).
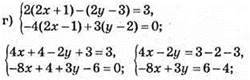
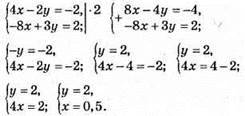
Відповідь: (0,5; 2).
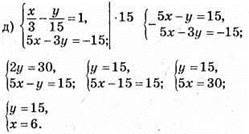
Відповідь: (6; 15).
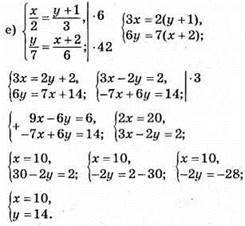
Відповідь: (10; 14).
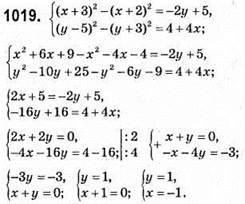
Відповідь: (-1; 1).
1020. Нехай фермер відвів під овочеві культури х га землі, тоді під зернові (х + 27) га землі. За умовою задачі х + х + 27 = 32; 2x = 32 – 27; 2x = 5; x = 2,5 га – відведено під овочеві культури; 2,5 + 2 7 = 29,5 га – відведено під зернові культури.
Відповідь: 29,5 га; 2,5 га.
1021. Нехай х грн. коштує 1 тонкий зошит і у грн. – 1 товстий зошит.
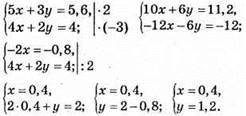
Відповідь: 40 коп.; 1 грн. 20 коп.
1022. Нехай Андрій має х монет по 10 к. і у монет по 25 к. 3 грн. 80 коп. = 380 коп.
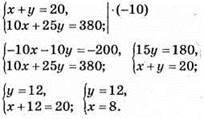
Відповідь: 8 і 12 монет.
1023. Нехай маса мішка першого гатунку х кг, другого – у кг.
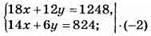
18 – 4 = 14 (мішків) – 1 гатунку залишилося;
12 – 6 = 6 (мішків) – 2 гатунку залишилося.
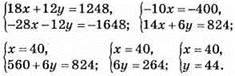
Відповідь: 40 кг; 44 кг.
1024. Нехай х і у числа.
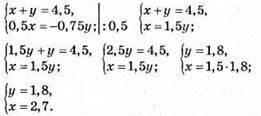
Відповідь: 2,7 і 1,8.
1025. Нехай швидкість автобусів буде х км/год, а автомобіля – у км/год.
10 год – 9 год 15 хв = 9 год 60 хв – 9 год
15 хв = 45 хв = 45/60 = 3/4 год.
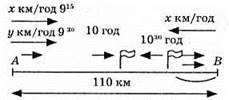
10 год – 9 год 30 хв = 9 год 60 хв – 9 год
30 хв = 30 хв = 30/60 = 1/2 год.
10 год 30 хв – 9 год 15 хв = 1 год 15 хв =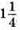 
год.
10 год 30 хв – 9 год 30 хв = 1 год.
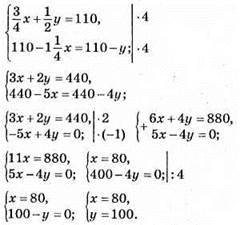
Відповідь: 80 км/год; 100 км/год.
1026.
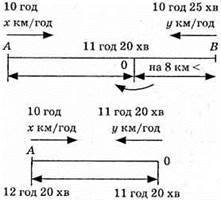
Х км/год – швидкість автобуса; у км/год – швидкість автомобіля.
11 год 20 хв – 10 год = 1 год 20 хв =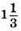 
год;
11 год 20 хв – 10 год 25 хв = 10 год 80 хв – 10 год 25 хв = 55 хв = 55/60 = 11/12 год;
12 год 20 хв – 11 год 20 хв = 1 год.
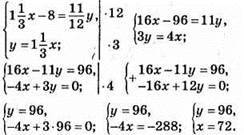
Відповідь: 72 км/год; 96 км/год.
Завдання для самоперевірки № 7
Рівень 1
1. Розв’язком рівняння х – y = 2 є пара чисел (3; 1).
Відповідь: б.
2. Розв’язком системи рівнянь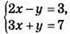 
є пара чисел (2; 1).
Відповідь: в.
3. 
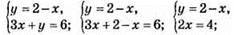
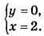
Відповідь: в) (2; 0).
4. 
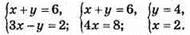
Відповідь: в) (4; 2).
5. Відповідь: г).
Рівень 2
6. (3; -3) і (2,6; 2) – розв’язки рівняння 5х – 2у = 9.
7. 
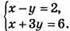Побудуємо в одній системі координат графіки рівнянь:
Х – y = 2 і х + 3y = 6
X | 0 | 2 | X | 0 | 3 |
Y | -2 | 0 | Y | 2 | 1 |
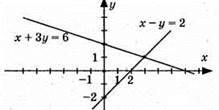
Координати точки перетину графіків – розв’язок системи рівнянь.
Відповідь: (3; 1).
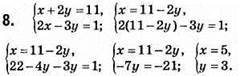
Відповідь: (5; 3).
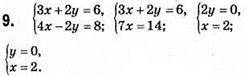
Відповідь: (2; 0).
10. Нехай велика упаковка борошна має масу х кг, а мала упаковка – у кг. Тоді
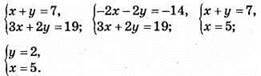
Отже, маса великої упаковки борошна 5 кг, а малої – 2 кг.
Рівень 3
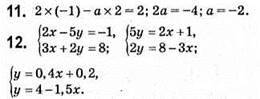
Будуємо графіки у = 0,4х + 0,2 і у = 4 – 1,5х.
X | 2 | 7 | X | 0 | 4 |
У | 1 | 3 | Y | 4 | -2 |
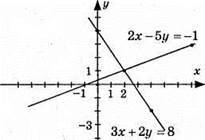
Координати точки перетину – розв’язок системи рівнянь.
Відповідь: (2; 1).
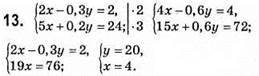
Відповідь: (4; 20).
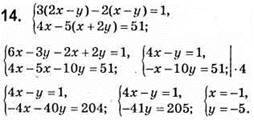
Відповідь: (-1; -5).
15. Нехай цукерки коштують x грн., печиво – у грн. Тоді
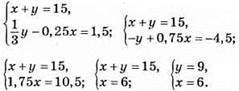
Відповідь: цукерки коштують 6 грн., печиво – 9 грн.
Рівень 4
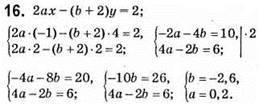
Відповідь: а = 0,2; b = -2,6.
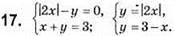
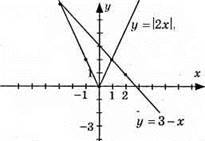
Побудуємо в одній системі координат графіки у = |2х| і y = 3 – х. Координати точок перетину – розв’язок системи рівнянь.
Відповідь: (1; 2); (-3; 6).
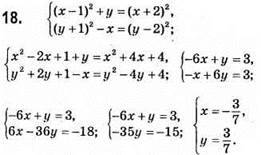
Відповідь: (-3/7; 3/7).
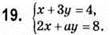Система має безліч розв’язків, коли 
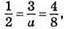тобто 3/2 = 1/2; а = 6.
20. Нехай сталі І сорту х т, а II сорту – у т. Тоді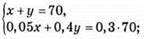 
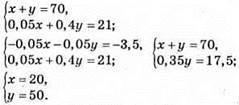
Відповідь: сталі І сорту 20 т; II сорту – 50 т.
(1 votes, average: 5.00 out of 5)
Loading...