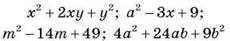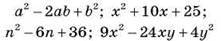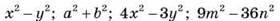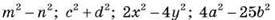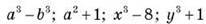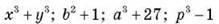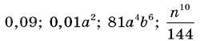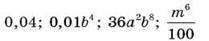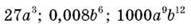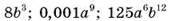ЗАСТОСУВАННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ ДО РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ
Цілі:
– навчальна: сформувати вміння розкладати многочлени на множники, використовуючи формули скороченого множення;
– розвивальна: формувати вміння орієнтуватися у видозміненій ситуації; розвивати творчі здібності, кмітливість учнів;
– виховна: виховувати інтерес до вивчення математики, наполегливість у досягненні мети;
Тип уроку : засвоєння нових знань, умінь, навичок.
Обладнання та наочність:
Хід уроку
І. ОРГАНІЗАЦІЙНИЙ ЕТАП
______________________________________________________
______________________________________________________
______________________________________________________
ІІ.
1. Перевірка завдання, заданого за підручником
______________________________________________________
______________________________________________________
2. Розв’язування задач
Колективне розв’язування задач, аналогічних до тих, що були задані додому
______________________________________________________
______________________________________________________
Індивідуальні завдання
№ 1
1) Розв’яжіть рівняння: x3 – x2 + x – 1 = 0.
2) Доведіть тотожність bn+1 + bn + b + 1 = (bn + 1)(b + 1).
№ 2
1) Розв’яжіть рівняння x3 + x2 + x + 1 = 0.
2) Доведіть тотожність am+2 – 1 – a + am+1 = (am+1 – 1)(a +1).
№ 3
1) Розв’яжіть рівняння
2) Доведіть тотожність xm+1 – xm + x – 1 = (x – 1)(xm + 1).
№ 4
1) Розв’яжіть рівняння x3 + 7×2 + 3x + 21 = 0.
2) Доведіть тотожність yn+2 + yn+1 – y – 1 = (y + 1)(yn+1 – 1).
III. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
Математичний диктант
Варіант 1 | Варіант 2 |
1. Запишіть многочлени: | |
|
|
Закресліть ті з них, які неможливо подати у вигляді квадрата двочлена. Подайте у вигляді квадрата двочлена ті вирази, які залишились | |
2. Запишіть многочлени: | |
|
|
Закресліть ті з них, які неможливо подати у вигляді добутку суми і різниці двох виразів. Ті многочлени, які залишились, подайте у вигляді добутку суми й різниці двох виразів | |
3. Запишіть многочлени: | |
|
|
Закресліть ті з них, які неможливо подати у вигляді добутку суми (різниці) і неповного квадрата різниці (суми) двох виразів. Ті многочлени, які залишились, подайте у вигляді такого добутку | |
4. Подайте у вигляді квадрата одночлена вирази: | |
|
|
5. Подайте у вигляді куба одночлена вирази: | |
|
|
IV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
План вивчення теми
Приклади розкладання многочленів на множники з використанням формул: 1) квадрата двочлена; 2) різниці квадратів; 3) суми й різниці кубів.
______________________________________________________
______________________________________________________
V. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І ВМІНЬ
Робота за підручником
______________________________________________________
______________________________________________________
VI. ПІДСУМКИ УРОКУ
1.
______________________________________________________
______________________________________________________
2. Фронтальне опитування
1) Наведіть приклад многочлена, який можна подати у вигляді:
А) квадрата суми; б) квадрата різниці.
2) На які множники можна розкласти різницю квадратів двох виразів? Наведіть приклади.
3) Як можна розкласти на множники:
А) різницю кубів; б) суму кубів? Наведіть приклади.
VII. ДОМАШНЄ ЗАВДАННЯ
1. Завдання за підручником:
______________________________________________________
______________________________________________________
2. Додаткове завдання. Розв’яжіть рівняння 2a(5a + 10) + (2a – 8)(3a + 2) = 0.
Відповідь. -1; 1.