Застосування різних способів розкладання многочлена на множники
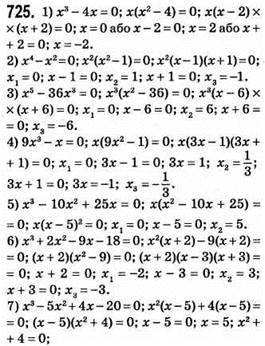
Немає коренів.
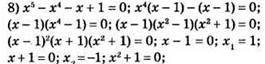
Немає коренів.
726. 1) х3 – х = 0; х(х2 – 1) = 0; х(х – 1)(х + 1) = 0; х = 0 або х – 1 = 0; х = 1 або х + 1 = 0; х = -1.
2) х4 + х2 = 0; х2(х2 + 1) = 0; х2 = 0; х = 0; х2 + 1 = 0; немає коренів.
3) х4 – 8х3 = 0; х3(х – 8) = 0; х, = 0; х – 8 = 0; Х2 = 8.
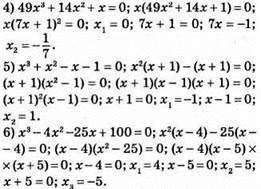
727. 1) (a – 1)3 – 9(а – 1) = (а – 1)(а – 4)(а + 2) – тотожність;
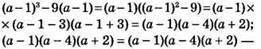Правильна рівність.
2)
(х2 + 1)2 – 4х2 = (х2 + 1 – 2х)(х2 + 1 + 2х) = (х – 1)2(х + 1)2;
(х – 1)2(х + 1)2 = (х – 1)2(х + 1)2 – рівність правильна.
728. 1) (а + 2)3 – 25(а + 2) = (а + 2)(а + 7)(а – 3) – тотожність;
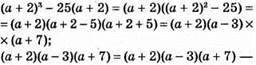правильна рівність.
2) а2 + 2ab + b2 – с2 + 2cd – d2 = (a + b + c – d)(а + b – с + d) – тотожність;
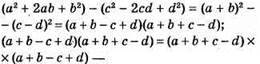
Правильна рівність.
729. 1) 1 спосіб: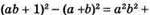 
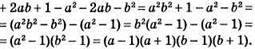
2 спосіб: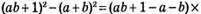 
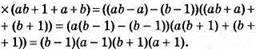
2) 1 спосіб: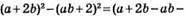 
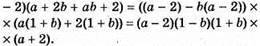
2 спосіб: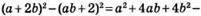 
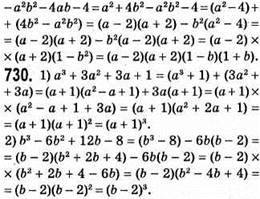
731. 1) (a + b + c)3 – a3 – b3 – c3 = 3(a + b)(b + c)(a + c) – тотожність;
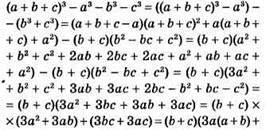
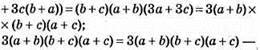правильна рівність.
2) (а – b)3 + (b – с)3 – (а – с)3 = -3(а – b)(b – с)(а – с) – тотожність;
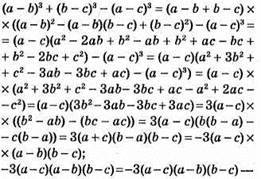правильна рівність.
Ділиться на 16, бо 8n(n2 + 1) ділиться на 16 і 16n2 ділиться на 16, бо 16 ділиться на 16.
Якщо n – непарне, то n2 + 1 – парне. Якщо n – парне, то n2 + 1 – непарне. Тобто один з множників n і n2 + 1 ділиться на 2.
Тоді 8n(n2 + 1) ділиться на 16.
(див. № 739 (2)).
Оскільки n4 + n2 + 1 розкладається на множники (n2 – n + 1) і (n2 + n + 1), відмінні від 1 і самого цього числа, то n4 + n2 + 1 має більш ніж два дільника, тому є числом складеним.
742. Нехай х, х + 4, х + 8, тоді за умовою:
Х(х + 8) + 88 = (х + 4)(х + 8); х2 + 8х + 88 = х2 + 4х + 8х + 32; 4х = 56; х = 14.
14, 18, 22 – шукані числа.
743. Нехай х год тривав шлях на гору, тоді шлях з гори тривав (4 – х) год. Шлях на гору становить 2,5х км, а з гори 4(4 – х) км.
За умовою 4(4 – х) – 2,5х = 3; 16 – 4х – 2,5х = 3; -6,5х = 3 – 16; -6,5х = -13; х = -13 : (-6,5); х = 2 год тривав шлях на гору.
4 – х = 4 – 2 = 2 год шлях з гори.
2,5 • 2 + 4 • (4 – 2) = 5 + 4 • 2 = 13 км увесь шлях.
744. 1) |7х – 3| = 4;
7х – 3 = 4; 7х = 4 + 3; 7х = 7; х = 7 : 7; х = 1; або 7х – 3 = -4; 7х = -4 + 3; 7х = -1; x = -1 : 7; x = -1/7.
2) ||х| – 10| = 8;
|х| – 10 = 8; |х| = 8 + 10; |х| = 18; х = 18 або х = -18;
Або |х| – 10 = -8; |х| = -8 + 10; |х| = 2; х = 2 або х = -2.
3) 4(х – 2) + 5|х| = 10; 4х – 8 + 5|х| = 10;
Х > 0: 4х – 8 + 5х = 10; 9х = 10 + 8; 9х = 18; х = 18 : 9; х = 2;
Х < 0: 4х – 8 – 5х = 10; – х = 10 + 8; – х = 18; х = -18;
4) |х|= 3х – 8;
Х > 0: х = 3х – 8; х – 3х = -8; -2х = -8; х = -8 : (-2); х = 4;
Х < 0: – х = 3х – 8; – х – 3х = -8; -4х = -8; х = -8 : (-4); х = 2 – не задовольняє умові х < 0.
745. 
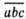+ 2(a + b + c) = 100а + 10b + с + 2а + 2b + 2с = 102а + 12b + 3с = 3 • (34а + 4b + с); ділиться націло на 3.
746. y = 0,2х – 3.
1) Якщо х = 4, то у = 0,2х – 3 = 0,2 • 4 – 3 = 0,8 – 3 = -2,2.
2) Якщо х = -3, то у = 0,2х – 3 = 0,2 • (-3) – 3 = -0,6 – 3 = -3,6.
747. А(2; 2); В(5; 1); С(0; -5); D(2; -3); Е(-1; -1); F(-5; 0); K(-4; 3); М(-3; 2); N(-4; -3).
748.
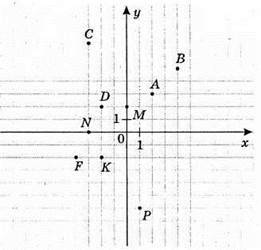
А(2; 3); В(4; 5); С(-3; 7); D(-2; 2); К(-2; -2); М(0; 2); N(-3; 0); Р(1; -6); F(-4; -2).
749.
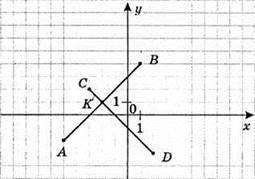
Відрізок АВ перетинає відрізок CD у точці K(-2; 1).
750. 1) Точка А(2; 6) розміщена вище осі х;
2) точка В(-3; 1) розміщена вище осі х;
3) точка С(-4; -5) розміщена нижче осі х;
4) точка D(-3; 0) розміщена на осі х.
751.
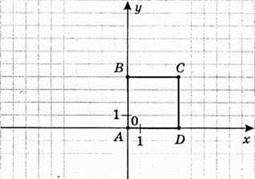
1 розв’язок: А(0; 0); В(0; 4); С(4; 4); D(4; 0). Сторони AB і AD лежать на осях координат, а добуток координат вершини С – додатне число: 4 • 4 > 0.
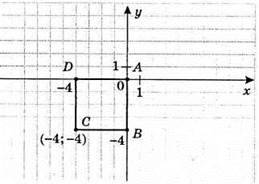
2 розв’язок: А(0; 0); В(0; -4); С(-4; -4); D(-4; 0). Сторони АВ і AD лежать на осях координат, а добуток координат вершини С – додатне число. -4 • (-4) = 16; 16 > 0.
(1 votes, average: 5.00 out of 5)
Loading...