Знаходження числа за його відсотками
Розділ II ДРОБОВІ ЧИСЛА І ДІЇ З НИМИ
§ 5. ДЕСЯТКОВІ ДРОБИ
38. Знаходження числа за його відсотками
У попередньому пункті ми навчилися знаходити відсотки від даного числа.
Розглянемо ще один вид задач на відсотки.
ПРИКЛАД 1 Вершкове морозиво містить 14 % цукру. Скільки кілограмів морозива виготовили, якщо було використано 49 кг цукру?
Розв’язання. 1) 49 : 14 = 3,5 (кг) – становить 1 % усієї маси морозива.
2) 3,5 ∙ 100 = 350 (кг) – виготовили морозива.
Відповідь: 350 кг.
У цій задачі ми знайшли число 350, знаючи, що число 49 становить
ПРИКЛАД 2 За день робітник виготовив 48 деталей, що становить 120 % кількості деталей, яку він мав виготовити за планом. Скільки деталей робітнику потрібно було виготовити за планом?
Розв’язання. 1) 48 : 120 = 0,4 (деталі) – становить 1 % плану.
2) 0,4 ∙ 100 = 40 (деталей) – треба було виготовити за планом.
Відповідь: 40 деталей.
ПРИКЛАД З У гаю ростуть дуби, клени та берези. Дуби становлять 15 % усіх дерев, клени – 23 %, а беріз росте 248. Скільки всього дерев росте в гаю?
Розв’язання. 1) 15 + 23 = 38 (%) – усіх дерев становлять
2) 100 – 38 = 62 (%) – усіх дерев становлять берези.
3) 248 : 62 = 4 (дерева) – становлять 1 % усіх дерев.
4) 4 ∙ 100 = 400 (дерев) – росте в гаю.
Відповідь: 400 дерев.
Розв’язуємо усно
1. Знайдіть числа, яких не вистачає в ланцюжку обчислень:
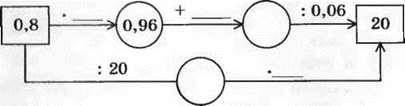
2. Золоту медаль за успіхи в навчанні отримали 14 випускників, що становить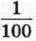 
усіх учнів школи. Скільки учнів у цій школі?
3. Вік Світланки становить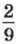 
віку її батька. Скільки років батькові, якщо Світланці 8 років?
4. Яку частину числа становлять:
1) 50 % цього числа; 3) 10 % цього числа;
2) 25 % цього числа; 4) 2 % цього числа?
5. Розв’яжіть рівняння:
1) 4х – 2,6х = 42; 2) 3,9х + 4,2х = 0,81.
В. Порівняйте 40 % числа 80 і 80 % числа 40.
7. Одне число становить 50 % другого. У скільки разів друге число більше за перше?
Вправи
1095.° Заповніть таблицю:
1 % числа | Дане число |
6 | |
3 | |
4,2 | |
7,68 |
1096.° Знайдіть число, якщо:
1) 20 % цього числа дорівнюють 40;
2) 54 % цього числа дорівнюють 81;
3) 280 % цього числа дорівнюють 70.
1097.° Знайдіть число, якщо:
1) 1 % цього числа дорівнює 7;
2) 1 % цього числа дорівнює 0,36;
3) 12 % цього числа дорівнюють 4,8;
4) 104 % цього числа дорівнюють 260.
1098.° За перший тиждень турист пройшов 32 км, що становить 40% туристського маршруту. Скільки кілометрів становить довжина маршруту?
1099.° Батько купив синові іграшку вартістю 27 грн, що становить 1,5 % його заробітної плати. Обчисліть заробітну плату батька.
1100.° Руда містить 60 % заліза. Скільки тонн руди треба взяти, щоб вона містила 72 т заліза?
1101.° Розчин містить 14 % солі. Скільки кілограмів розчину треба взяти, щоб він містив 49 кг солі?
1102.° Банк сплачує своїм вкладникам 8 % річних. Скільки грошей треба покласти в банк, щоб через рік отримати 60 грн прибутку?
1103. °Маса сушених слив становить 15 % маси свіжих. Скільки треба взяти свіжих слив, щоб отримати 36 кг сушених?
1104.° За тиждень бригада робітників відремонтувала 138 м дороги, що становить 115 % плану. Скільки метрів дороги планували відремонтувати за тиждень?
1105.° На обід Карлсон з’їв 28,8 кг варення, що становило 120 % того, що він планував з’їсти. Скільки варення планував з’їсти Карлсон на обід?
1106.°Під час сушіння яблука втрачають 84 % своєї маси. Скільки треба взяти свіжих яблук, щоб одержати 24 кг сушених?
1107.° Під час тушкування м’ясо втрачає 24 % своєї маси. Скільки треба взяти сирого м’яса, щоб отримати 19 кг тушкованого?
1108.° На обід у харчевні “Три піскарі” лисиця Аліса та кіт Базиліо замовили салат “Олів’є”, смажене порося і торт з морозива. Коли їм принесли рахунок, то виявилось, що за салат треба заплатити 28 % суми, за порося – 54 %, а за торт – решту 108 сольдо. Скільки сольдо коштував обід Аліси та Базиліо?
1109.°Троє друзів збирали гриби. Перший зібрав 37 % усіх грибів, другий – 25 %, а третій – решту 76 грибів. Скільки всього грибів вони зібрали?
1110.° Довжина прямокутного паралелепіпеда дорівнює 50 см, а ширина становить 24 % довжини. Обчисліть об’єм паралелепіпеда, якщо ширина становить 30 % висоти.
1111.° Площа біосферного заповідника Асканія-Нова (Херсонська область) дорівнює 11,1 тис. га. Площа природного заповідника Медобори (Тернопільська область) становить 94 % площі заповідника Асканія-Нова і 25 % площі природного національного парку Синевир (Закарпаття). Знайдіть площу заповідника Медобори і площу парку Синевир.
1112.°За перший день турист пройшов 7,2 км, за другий день – 150 % того, що за перший. Скільки кілометрів пройшов турист за три дні, якщо за другий день він пройшов 90 % того, що за третій?
1113.°°У саду ростуть яблуні та вишні, причому яблуні становлять 41 % усіх дерев. Вишень росте на 54 дерева більше, ніж яблунь. Скільки дерев росте в саду? Скільки серед них є вишень?
1114.°° За два дні було прокладено кабель. За перший день проклали 68 % довжини кабелю, а за другий – на 115,2 м менше, ніж за перший. Скільки всього метрів кабелю було прокладено за два дні? Скільки метрів кабелю проклали за перший день?
1115.°° У саду ростуть кущі червоних, рожевих і білих троянд. Червоні троянди становлять 40 % усіх кущів, рожеві – 58 % решти, а білих троянд росте 126 кущів. Скільки всього кущів троянд росте в саду?
1116.°° За перший день Василько прочитав 25 % усієї книжки, за другий – 68 % остачі, а за третій – решту 96 сторінок. Скільки сторінок у книжці?
1117.°°Скільки кілограмів картоплі продав магазин за три дні, якщо за перший день продали 32 % маси всієї картоплі, за другий – 45 % маси остачі, а за третій – 561 кг?
1118.°На новорічне свято до школи завезли три види морозива: шоколадне, суничне та ванільне. Шоколадне становило 52 % маси всього морозива, суничне – 25 % маси шоколадного, а ванільне – решту 140 кг. Скільки кілограмів морозива завезли до школи?
1119.° У саду Барвінка росли айстри, гладіолуси та жоржини. Айстри становили 60 % усіх квітів, гладіолуси – 40 % кількості айстр, а жоржин було 32 квітки. Скільки айстр росло в саду Барвінка?
Вправи для повторення
1120. Заповніть пропуски в ланцюжку обчислень, якшо: 1) х = 2.6: 2) х = 8.
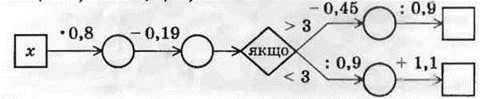
1121. Розв’яжіть рівняння:
1) 0,31х + 1,2 = 1,2124;
2) 0,5х – 17 = 40,52;
3) 4,6 – 0,03х = 1,3;
4) 0,4х + 0,24х – 0,26 = 0,764.
1122. За даними перепису населення у 2001 р. в Україні кількість людей, які мали вищу освіту, становила 113,6 % порівняно з аналогічним показником у 1989 р. Скільки людей у 2001 р. мали вищу освіту, якщо в 1989 р. їх було 12 048 000 осіб? Відповідь округліть до тисяч.
1123. За даними перепису населення в 1989 р. в Україні з кожних 1000 осіб у віці 10 років і старших повну середню освіту мали 295 осіб, у 2001 р. цей показник становив 122,5 % порівняно з аналогічним показником у 1989 р. Скільки людей із кожної тисячі мали повну середню освіту у 2001 p.? Відповідь округліть до одиниць.
1124. Від двох пристаней, відстань між якими дорівнює 63 км, одночасно назустріч один одному відійшли два моторних човни. Швидкість одного з них 16 км/год. Човни зустрілися через 2 год 6 хв після початку руху. Знайдіть швидкість другого човна.
1125. Скільки існує двоцифрових чисел, у записі яких використано тільки: 1) цифри 0, 2, 4, 6 і 8; 2) цифри 1, 3, 5, 7 і 9? (Цифри можуть повторюватися.
Задача від Мудрої Сови
1126. Для перегляду кінофільму в залі для глядачів зібрались учні кількох шкіл. Виявилося, що учні однієї із шкіл становлять 47 % кількості глядачів. Скільки всього глядачів було в залі, якщо в ньому 280 місць і понад половину місць було зайнято?
ЗАВДАННЯ № 6 “ПЕРЕВІРТЕ СЕБЕ” В ТЕСТОВІЙ ФОРМІ
1. Скільки цифр записано справа від коми в добутку чисел 2,64 і 3,72?
А) дві цифри В) чотири цифри
Б) три цифри Г) п’ять цифр
2. Чому дорівнює половина однієї сотої?
А) 0,5 Б) 0,002 В) 0,02 Г) 0,005
3. Спростіть вираз 0,2а ∙ 1,5b.
А) 3ab Б) 0,Заb В) 0,03аb Г) 30аb
4. Чому дорівнює значення виразу 48 : (1,07 + 0,53) -1,6?
А) 28,4 Б) 1,4 В) 27,4 Г) 1,54
5. Спростіть вираз 2,1с – 0,6с + 3,9с.
А) 5,4с Б) 6,6с В) 5,8с Г) 5,2с
6. Чому дорівнює значення виразу (36 – 1,8 ∙ 2,7): 0,9?
А) 14 Б) 1,4 В) 3,46 Г) 34,6
7. У стаді було 200 тварин, з яких 34 % становили вівці. Скільки овець було в стаді?
А) 54 вівці Б) 68 овець В) 72 вівці Г) 86 овець
8. Сплав містить 28 % міді. Яка маса злинка сплаву, якщо він містить 56 кг міді?
А) 350 кг Б) 300 кг В) 250 кг Г) 200 кг
9. Велосипедист проїхав 20 км зі швидкістю 10 км/год і 15 км зі швидкістю 5 км/год. Знайдіть середню швидкість руху велосипедиста.
А) 6 км/год В) 7,5 км/год
Б) 7 км/год Г) 9 км/год
10. Десять автобусних зупинок розміщені на прямій вулиці так, що відстані між будь-якими сусідніми зупинками однакові. Відстань між першою і третьою зупинками дорівнює 1,2 км. Яка відстань між першою і останньою зупинками?
А) 12 км Б) 10,8 км В) 5,4 км Г) 6 км
11. На яке найменше натуральне число треба помножити число 3,6, щоб добуток був натуральним числом?
А) 2 Б) 5 В) 10 Г) 20
12. До магазину завезли яблука та груші, причому груші становили 35 % завезених фруктів. Яблук було на 126 кг більше, ніж груш. Скільки всього кілограмів яблук і груш завезли до магазину?
А) 300 кг Б) 350 кг В) 420 кг Г) 480 кг.
ГОЛОВНЕ В ПАРАГРАФІ 5
Властивості десяткового дробу
– Якщо до десяткового дробу справа приписати будь-яку кількість нулів, то отримаємо дріб, який дорівнює даному.
– Значення дробу, який закінчується нулями, не зміниться, якщо останні нулі в його записі відкинути.
Порівняння десяткових дробів
– Із двох десяткових дробів більший той, у якого ціла частина більша.
– Щоб порівняти два десяткових дроби з рівними цілими частинами та різною кількістю цифр після коми, треба за допомогою приписування нулів справа зрівняти кількість цифр у дробових частинах, після чого порівняти отримані дроби порозрядно.
Округлення десяткових дробів
Для того щоб десятковий дріб округлити до одиниць, десятих, сотих і т. д., треба всі наступні за цим розрядом цифри відкинути. Якщо при цьому перша з цифр, які відкидають, дорівнює 0, 1, 2, З або 4, то останню з цифр, які залишають, не змінюють; якщо ж перша з цифр, які відкидають, дорівнює 5, 6, 7, 8 або 9, то останню з цифр, які залишають, збільшують на одиницю.
Округлення натуральних чисел
При округленні натуральних чисел до деякого розряду замість усіх наступних за цим розрядом цифр молодших розрядів пишуть нулі. Якщо перша з цифр, що йшли за цим розрядом, дорівнює 0, 1, 2, 3 або 4, то цифру в даному розряді не змінюють; якщо ж перша з цифр, що йшли за цим розрядом, дорівнює 5, 6, 7, 8 або 9, то цифру в даному розряді збільшують на одиницю.
Додавання десяткових дробів
Щоб знайти суму двох десяткових дробів, треба:
1) зрівняти в доданках кількість цифр після ком;
2) записати доданки один під одним так, щоб кожний розряд другого доданка опинився під відповідним розрядом першого доданка;
3) додати отримані числа так, як додають натуральні числа;
4) поставити в отриманій сумі кому під комами в доданках.
Віднімання десяткових дробів
Щоб знайти різницю двох десяткових дробів, треба:
1) зрівняти в зменшуваному і від’ємнику кількість цифр після ком;
2) записати від’ємник під зменшуваним так, щоб кожний розряд від’ємника опинився під відповідним розрядом зменшуваного;
3) виконати віднімання так, як віднімають натуральні числа;
4) поставити в отриманій різниці кому під комами в зменшуваному і від’ємнику.
Множення десяткових дробів
Щоб перемножити два десяткових дроби, треба:
1) перемножити їх як натуральні числа, не звертаючи уваги на коми;
2) в отриманому добутку відокремити комою справа стільки цифр, скільки їх стоїть після ком в обох множниках разом.
– Щоб помножити десятковий дріб на 10, 100, 1000 і т. д., треба в цьому дробі перенести кому вправо відповідно на 1, 2, 3 і т. д. цифри.
– Щоб помножити десятковий дріб на 0,1; 0,01; 0,001 і т. д., треба в цьому дробі перенести кому вліво відповідно на 1, 2, 3 і т. д. цифри.
Ділення десяткових дробів
– Щоб поділити десятковий дріб на десятковий, треба:
1) перенести в діленому і в дільнику коми вправо на стільки цифр, скільки їх міститься після коми в дільнику;
2) виконати ділення на натуральне число.
– Щоб поділити десятковий дріб на 10, 100, 1000 і т. д., треба в цьому дробі перенести кому вліво на 1, 2, 3 і т. д. цифри.
Середнє арифметичне
Середнім арифметичним кількох чисел називають частку під ділення суми цих чисел на кількість доданків.
Відсоток (процент)
Відсотком (процентом) називають соту частину величини або числа.
Вправи для повторення за курс 5 класу
1127. Виконайте дії:
1) 154 ∙ 78 + 3900 : 65 – 216 ∙ 53;
2) 16 728 : 82 – 5580 : 45 4- 726 ∙ 29;
3) (39 002 – 37 236) ∙ 205 + 115 ∙ 78;
4) 875 ∙ 480 – 406 ∙ (50 004 – 48 986);
5) (21 518 : 53 – 24 332 : 79) ∙ 267;
6) (53 734 : 67 – 59 925 : 85) ∙ 436;
7) (327 ∙ 84 + 207 673) : 47;
8) (924 -93 + 30 271) : 29;
9) (216 ∙ 28 – 463 680 : 92) : (86 ∙ 64 – 4496);
10) (1004 ∙ 19 – 75 110 : 37) : (408 ∙ 435 – 177 479);
11) 61 -(1428 : 136 + 4,3) ∙ 3,4;
12) 40 – (2550 : 204 – 6,9) ∙ 6,7;
13) 37,72 : 4,6 – (1,43 + 2,728) ∙ 1,5;
14) 7,2 ∙ 3,8 + (3,24 – 2,1312) : 0,42;
15) 3,564 : 0,66 + 0,4992 : 0,052 – 83 – 0,107;
16) 98 ∙ 0,035 – 0,0288 : 0,36 – 3 : 16;
17) (0,084 ∙ 4,8 – 0,2132 : 6,5 + 0,0296) : 0,625;
18) (0,056 ∙ 7,4 + 4,2106 : 7,4 – 0,0834) : 0,375;
19) (20,6 – 16,74) ∙ 0,1 + (23,4 + 8,95) : 100;
20) (0,326 + 3,724) ∙ 100 – (0,19682 – 0,0987) : 0,001;
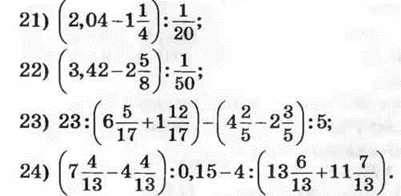
1128. Складіть числовий вираз і знайдіть його значення: 1) різниця суми чисел 17,23 і 16,37 та різниці чисел 9 і 6,328;
2) різниця різниці чисел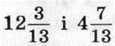 
та суми чисел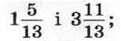 
3) добуток суми чисел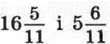 
та числа 3,245;
4) частка різниці чисел 4,8 і 3,762 та числа 0,06;
5) добуток суми чисел 3,47 і 3,46 та їх різниці;
6) частка різниці чисел 6,3 і 4,2 та їх суми;
7) сума добутку чисел 0,125 і 16 та частки чисел 28 і 0,56;
8) різниця частки чисел 0,128 і 0,4 та частки чисел 0,126 і 0,6;
9) частка суми чисел 86,9 і 667,6 та суми чисел 37,1 і 13,2;
10) добуток суми чисел 1,367 і 6,033 та різниці чисел 12 і 11,15.
1129. На скільки:
1) різниця чисел 6,2 і 1,4 менша від їх добутку;
2) різниця чисел 11,88 і 2,64 більша за їх частку;
3) сума чисел 7,8 і 6,5 більша за їх частку;
4) добуток чисел 7,6 і 0,8 менший від різниці цих чисел;
5) добуток чисел 14,5 і 1,06 більший за різницю чисел 16,1 і 4,386;
6) частка чисел 2 і 250 більша за добуток чисел 0,18 і 0,04?
1130. 1) Запишіть чотири числа, перше з яких дорівнює 3,24, а кожне наступне в 10 разів більше за попереднє.
2) Запишіть п’ять чисел, перше з яких дорівнює 430, а кожне наступне в 10 разів менше від попереднього.
1131. Знайдіть значення виразу:
1) 72 : (x – 17) – 4, якщо де = 35;
2) (x + 259) : (x – 205), якщо х = 321;
3) 61,32 – 61,32 : (а + b), якщо а = 3,6, b = 4,8;
4) 4,346 : х – у : 0,25, якщо х = 0,82, у = 0,4;
5) 2,04 : х + 5,19у, якщо x = 3,4, у = 0,4;
6) 1,4m – 0,3n, якщо m = 2,6, n = 5,09;
7) 1000x + 0,01 у, якщо x = 0,2346, у = 26 540;
8) 453x – 0,1827y, якщо x = 0,1, у = 100;
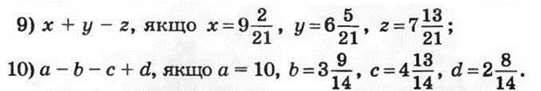
1132. Розв’яжіть рівняння:
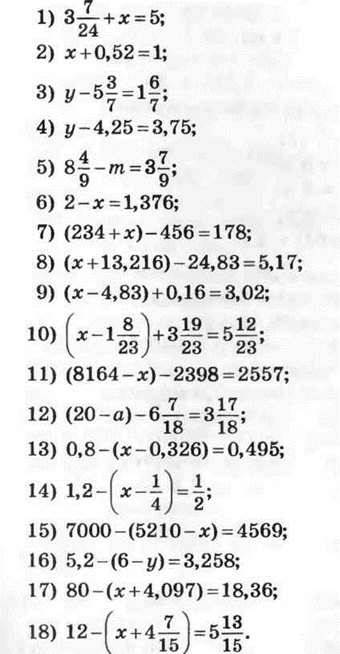
1133. Розв’яжіть рівняння:
1) 0,11x + 0,08x = 45,6;
2) 2,9x – 1,1x = 5,04;
3) x – 0,64x = 2,808;
4) 7x + 9х + 0,32 = 2,72;
5) 5у + 7у – 0,024 = 0,204;
6) 2,4x – 1,5x + 47 = 1919;
7) 0,8 (x – 1,9) = 0,56;
8) 0,32 (x + 1,4) = 73,6;
9) 1,7 (5x – 0,16) = 0,238;
10) 0,8 (100 – 0,04x) = 8,64;
11) x : 1,15 = 0,16;
12) 0,408 : x = 1,7;
13) (x + 9,14) : 7,2 = 5;
14) 2,2 – x : 0,3 = 0,13;
15) 5,6 : (x + 1,6) = 0,08;
16) 5,6 : x + 0,16 = 0,3;
17) 4,13 – 1,7x = 4,028;
18) 61 : (2,4у + 19,04) = 3,2.
1134. 1) До якого числа треба додати 4,2, щоб добуток отриманої суми і числа 0,6 дорівнював 19,2?
2) Під якого числа треба відняти 9,4, щоб добуток отриманої різниці і числа 0,5 дорівнював 0,12?
3) На яке число треба помножити 12,3, щоб сума отриманого добутку і числа 7,9 дорівнювала 12,82?
4) Яке подвоєне число треба відняти від 20,04, щоб отримати 9,1?
5) Яке число треба помножити на 0,4, щоб сума отриманого добутку і числа 3,8 дорівнювала добутку чисел 20,5 і 4?
1135. Знайдіть числа, яких не вистачає в ланцюжку обчислень:
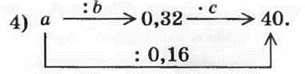
1136. Не виконуючи обчислень, порівняйте значення виразів:
1) 12 ∙ 0,34 і (12 ∙ 34) : 100;
2) 520 ∙ 0,05 і (520 ∙ 5) : 10;
3) 0,3 ∙ 0,9 і (3 ∙ 9) : 100;
4) 3,648 : 0,06 і 364,8 : 0,6.
1137. Не виконуючи обчислень, укажіть корінь рівняння:
1) х ∙ 0,86 = (7 ∙ 86) : 100;
2) 2,4у = (24 ∙ 16) : 100;
3) (54 ∙ z) : 10 = 5,4 ∙ 6;
4) а : 0,35 = (7,16 ∙ 100) : 35;
5) b: 6,5 = 130 : 65;
6) 46,2 : с = 0,462 : 0,0007.
1138. Знайдіть усі натуральні значення х, при яких буде правильною нерівність:
1) 2,4 < х < 6; 4) 11 < х < 13;
2) 3,2 < х < 8; 5) 1,2 < х < 1,9;
3) 9 < х < 14;
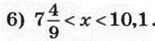
1139. Знайдіть найбільше натуральне значення х, при якому буде правильною нерівність:
1) 3х < 19,4; 2) 5х < 32,6.
1140. Знайдіть найменше натуральне значення х, при якому буде правильною нерівність:
1) 4х > 14;
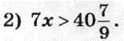
1141. Агрофірма “Саджай-збирай” виростила на двох полях жито. З одного поля зібрали 392 ц жита, а з другого – 896 ц. Площа другого поля на 18 га більша за площу першого. Знайдіть площу кожного поля, якщо врожайність з 1 га землі на цих полях однакова.
1142. Акціонерне товариство “Смачного” продало в суботу 46 коробок цукерок, а в неділю – 62 таких коробки. У неділю було продано на 120 кг цукерок більше, ніж у суботу. Скільки кілограмів цукерок було продано в суботу і скільки – у неділю?
1143. Коза-дереза зібрала з поля площею 2,3 га по 400 ц капусти з гектара. Скільки автомобілів вантажопідйомністю 3,5 т їй треба замовити для перевезення врожаю?
1144. Барвінок засіяв поле прямокутної форми пшеницею. Довжина поля дорівнювала 37,5 м, що в 1,5 раза більше за його ширину. Скільки центнерів пшениці зібрав Барвінок з усього поля, якщо з кожного ара він зібрав 42,8 ц? Запишіть отриману відповідь у тоннах, центнерах і кілограмах.
1145. Михайлик купив 6 тістечок і отримав 12,8 грн здачі. Для покупки 9 тістечок Михайлику не вистачило 8,8 грн. Скільки коштує одне тістечко?
1146. Чіп може з’їсти 360 тістечок за 18 хв, а Дейл ту саму кількість тістечок – за 12 хв. За скільки хвилин Чіп і Дейл зможуть з’їсти ці тістечка разом?
1147. Котигорошко може нарубати 300 м3 дров за 3 хв, а Івасик-Телесик ту саму кількість дров – за 6 хв. За скільки хвилин вони разом можуть нарубати стільки дров?
1148. Два насоси одночасно викачували воду з басейну. Один насос за хвилину викачував 200 л, а другий – 140 л. Скільки часу працювали насоси і скільки води викачав кожний із них, якщо перший насос викачав на 210 л більше, ніж другий?
1149. Маса цеберка з водою дорівнює 12,5 кг. Коли з цеберка вилили половину води, то маса цеберка з водою стала дорівнювати 7 кг. Яка маса порожнього цеберка?
1150. У принцеси Моди було 30 платтів і 24 маскарадних костюми, на пошиття яких витратили 163,5 м тканини. На кожне плаття витратили на 0,5 м тканини більше, ніж на кожний костюм. Скільки тканини витратили на одне плаття і скільки – на один костюм?
1151. У коморі було 15 ящиків і 12 кошиків, у яких зберігалося 576 кг яблук, причому в кожному ящику було на 6 кг яблук більше, ніж у кожному кошику. Скільки кілограмів яблук було в кожному ящику і скільки – у кожному кошику?
1152. На сніданок Вінні-Пух з’їв 7,5 кг меду, на обід – в 1,2 раза більше, ніж на сніданок, а на вечерю – 0,8 того, що з’їв на обід. Скільки кілограмів меду з’їв за день Вінні-Пух?
1153. 1) Автомобіль долає відстань між двома містами за 3,6 год, якщо рухається зі швидкістю 62,5 км/год. З якою швидкістю він має рухатись, щоб подолати цю відстань за 3 год?
2) Поїзд проходить відстань між двома станціями за 4,2 год, рухаючись зі швидкістю 54 км/год. За який час він пройде цю відстань, якщо рухатиметься зі швидкістю 63 км/год?
1154. Із двох станцій назустріч один одному одночасно вирушили два поїзди. Один поїзд проходить 14,7 км за кожні 
год, а другий – 22,4 км за
год. Через скільки годин після початку руху відстань між поїздами становитиме 37,8 км, якщо відстань між станціями дорівнює 138,6 км?
1155. З одного пункту в одному напрямі одночасно вирушили два пішоходи. Перший пішохід іде зі швидкістю 5,2 км/год, а другий – 4,3 км/год. Якою буде відстань між ними через 4 год після початку руху?
1156. З одного пункту в одному напрямі одночасно вирушили автомобіль і автобус. Автомобіль рухався зі швидкістю 72 км/год, а автобус – зі швидкістю 64 км/год. Через скільки годин після початку руху відстань між автомобілем і автобусом становила 52 км?
1157. З одного пункту в одному напрямі одночасно вирушили два вершники. Через 2 год після початку руху відстань між ними була 3 км. Швидкість одного з вершників дорівнює 8,2 км/год. Знайдіть швидкість другого вершника. Скільки розв’язків має задача?
1158. З одного пункту в протилежних напрямах одночасно виїхали автомобіль і автобус. Швидкість автомобіля дорівнює 72 км/год, а швидкість автобуса в 1,2 рала менша від швидкості автомобіля. Якою буде відстань між автомобілем і автобусом через 3 год 15 хв після початку руху?
1159. З одного пункту в протилежних напрямах одночасно вийшли два пішоходи. Швидкість одного з них 
дорівнює 4,2 км/год, що становить – швидкості другого. Через скільки годин після початку руху відстань між пішоходами дорівнюватиме 11,7 км?
1160. Від однієї станції в протилежних напрямах одночасно відійшли два поїзди. Через 2 год 45 хв після початку руху відстань між поїздами дорівнювала 330 км. Швидкість одного з поїздів становила 56 км/год. Знайдіть швидкість другого поїзда.
1161. Із двох пунктів, відстань між якими дорівнює 84 км, в одному напрямі виїхали одночасно два автомобілі зі швидкостями 68,4 км/год і 57,9 км/год. Автомобіль з меншою швидкістю рухався попереду. Через скільки годин після початку руху один автомобіль наздогнав другий?
1162. Із двох пунктів в одному напрямі вийшли одночасно два туристи. Турист, який рухався зі швидкістю 4,8 км/год, наздогнав туриста, який рухався зі швидкістю 4,2 км/год, через 2,5 год після початку руху. Знайдіть відстань між пунктами, з яких вийшли туристи.
1163. Із двох пунктів в одному напрямі одночасно виїхали велосипедист і мотоцикліст. Мотоцикліст, який їхав зі швидкістю 76,2 км/год, наздогнав велосипедиста, який їхав зі швидкістю 9,8 км/год, через 3,5 год після початку руху. Знайдіть відстань між велосипедистом і мотоциклістом до початку руху.
1164. Із двох пунктів, відстань між якими дорівнює 189 км, виїхали одночасно в одному напрямі вантажний і легковий автомобілі. Вантажний автомобіль їхав зі швидкістю 48 км/год, і через 7 год після початку руху його наздогнав легковий автомобіль. З якою швидкістю їхав легковий автомобіль?
1165. Із двох пунктів, відстань між якими дорівнює 111 км, одночасно в одному напрямі виїхали мотоцикліст і вершник. Мотоцикліст їхав зі швидкістю 82 км/год і наздогнав вершника через 1,5 год після початку руху. Знайдіть швидкість вершника.
1166. О 10 год з пункту виїхав вантажний автомобіль зі швидкістю 42,4 км/год. 0 13 год 30 хв із цього ж пункту в тому самому напрямі виїхав мотоцикліст зі швидкістю 78,5 км/год. Якою буде відстань між ними о 15 год 30 хв? о 18 год?
1167. Теплохід пройшов 237 км проти течії річки за 6 год. Який шлях він пройде в стоячій воді за 8 год, якщо швидкість течії дорівнює 1,5 км/год?
1168. Катер пройшов за течією річки 119 км за 3,5 год. Яку відстань він пройде за 5 год проти течії, якщо швидкість катера в стоячій воді становить 32,8 км/год?
1169. Швидкість теплохода за течією річки дорівнює 29,6 км/год, а проти течії – 24,8 км/год. Знайдіть швидкість течії і власну швидкість теплохода.
1170. Власна швидкість катера дорівнює 28 км/год, а швидкість течії річки – 1,8 км/год. Спочатку катер ішов 1,4 год проти течії, а потім 0,8 год за течією. Який шлях пройшов катер за весь цей час?
1171. Від двох пристаней одночасно назустріч один одному вирушили два катери. Через скільки годин вони зустрінуться, якщо власна швидкість кожного катера дорівнює 24,5 км/год, відстань між пристанями – 171,5 км, а швидкість течії – 1,6 км/год? Чи є в умові задачі зайві дані?
1172. Від двох пристаней одночасно назустріч один одному вирушили човен і теплохід. Човен, власна швидкість якого дорівнює 10,8 км/год, рухається за течією річки, а теплохід, власна швидкість якого – 30,2 км/год, рухається проти течії. Через скільки годин вони зустрінуться, якщо відстань між пристанями дорівнює 205 км?
1173. Рибалка переправлявся через річку на човні зі швидкістю 20 м/хв. На яку відстань човен буде віднесено за течією, якщо ширина річки дорівнює 150 м, а швидкість течії – 0,2 м/с?
1174. На спуск з гори турист витрачає 0,75 часу, який потрібен йому для підйому на цю гору. З гори він спускається за 1,2 год, а піднімається зі швидкістю 7,5 м/хв. Яка висота гори, на яку піднімається турист?
1175. Машиніст швидкого поїзда, що рухався зі швидкістю 56 км/год, помітив, що зустрічний товарний поїзд, який рухався зі швидкістю 34 км/год, пройшов повз нього за 15 с. Яка довжина товарного поїзда?
1176. Машиніст товарного поїзда, що рухався зі швидкістю 36 км/год, помітив, що зустрічний пасажирський поїзд, довжина якого 180 м, пройшов повз нього за 8 с. З якою швидкістю рухався пасажирський поїзд?
1177.0 9 год ранку Незнайко вирушив із Квіткового міста в Сонячне пішки зі швидкістю 3,6 км/год. 0 12 год 30 хв слідом за ним на всюдиході власної конструкції виїхали Гвинтик зі Шпунтиком. Всюдихід рухався зі швидкістю 12 км/год і прибув у Сонячне місто одночасно з Незнайком. Скільки часу йшов Незнайко? Яка відстань між містами Квіткове і Сонячне?
1178. Кіт Мурзик купив на базарі 18 кг сметани, а кіт Мурчик – 28 кг. На обід Мурзик з’їв 0,65 купленої сметани, а Мурчик –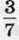 
своєї сметани. Хто з котів з’ їв більше сметани і на скільки кілограмів?
1179. Хлопчик-Мізинчик у чоботях-скороходах за З год подолав 1590 км. За першу годину він пройшов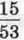 
цієї відстані, за другу годину – 
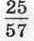решти. Скільки кілометрів він подолав за третю годину?
1180. Було зібрано 240 кг насіння соняшнику. Скільки соняшникової олії можна отримати із зібраного насіння, якщо маса зерна становить 0,7 маси насіння соняшнику, а маса отриманої олії – 0,4 маси зерна?
1181. Три велетні їли на обід куліш. Один із них з’їв 120 кг кулешу, другий –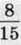 
того, що з’їв перший, а третій – 0,85 того, що з’їв другий. Скільки кілограмів кулешу з’їли велетні?
1182. Параметр трикутника дорівнює 48 см. Довжина однієї зі сторін трикутника становить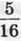 
периметра, а довжина другої – 0,64 довжини першої сторони. Знайдіть сторони трикутника.
1183. Основа рівнобедреного трикутника дорівнює 6,5 см, а довжина бічної сторони становить 0,8 довжини основи. Обчисліть периметр трикутника.
1184. Обчисліть:
1) 0,1 від суми чисел 34,56 і 7,94;
2) 
від різниці чисел 42,3 і 5,4;
3) 0,36 від добутку чисел 12,5 і 1,6;
4) 
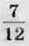від частки чисел 14,4 і 0,01.
1185. Середня тривалість життя білого ведмедя – 32 роки, що становить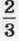 
середньої тривалості життя носорога, 
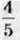– лева і 
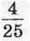– слона. Знайдіть середню тривалість життя носорога, лева і слона. 1186. Барвінок зібрав у своєму саду врожай фруктів. Яблука становили 0,6 маси зібраних фруктів. Яблук сорту білий налив було 35 кг, і вони становили 
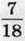маси всіх яблук. Скільки кілограмів фруктів зібрав Барвінок?
1187. Коли автомобіль проїхав 0,3, а потім ще 0,4 усього шляху, то виявилося, що він проїхав на 12 км більше за половину шляху, який треба було проїхати. Скільки кілометрів мав проїхати автомобіль?
1188. У двох ящиках лежали яблука. У першому ящику лежало 22,4 кг яблук, що становило 0,35 усіх яблук. Скільки кілограмів яблук було в другому ящику?
1189. За день продали 3,6 ц ковбаси, що становило 0,48 її запасів. Скільки центнерів ковбаси залишилось?
1190. Зореліт “Срібна блискавка” вилетів із космічної станції “Star” до станції “Мооn”. За першу годину зореліт подолав 48,72 млн кілометрів, що становило 0,56 того, що йому залишилося пролетіти. Знайдіть відстань між станціями.
1191. Попелюшка спекла пиріжки з маком і з вишня ми. Пиріжки з маком становили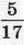 
їхньої загальної кількості. Скільки всього пиріжків спекла Попелюшка, якщо пиріжків з вишнями було на 28 більше, ніж з маком?
1192. Знайдіть число:
1) 0,8 якого становить суми чисел 19,4 і 20,64;
2) 
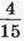якого становить різниця чисел 7 і 4,76;
3) 0,42 якого становить добуток чисел 7,2 і 3,5;
4) 
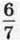якого становить частка чисел 0,54 і 0,9.
1193. На рисунку 213 кут DOE – прямий. Які із зображених кутів є тупими? Скільки гострих кутів зображено на цьому рисунку?
1194. Накресліть тупий кут і проведіть з його вершини промінь так, щоб утворився прямий кут. Скільки розв’язків має задача?
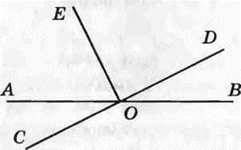
Рис. 213
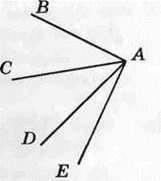
Рис. 214
1195. Знайдіть градусну міру кута ВАЕ, якщо ∠BAD = 67°, ∠CAD = 34°, ∠CAE = 56° (рис. 214).
1196. Кут МОК – розгорнутий, ∠MOA = 62°, промінь ОС – бісектриса кута АОК. Обчисліть градусну міру кута СОА.
1197. Запишіть усі трикутники і прямокутники, зображені на рисунку 215.
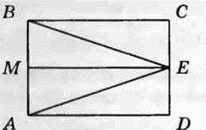
Рис. 215
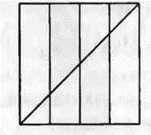
Рис. 216
1198. Периметр трикутника дорівнює 30 см, одна із його сторін – 7,4 см, а дві інші сторони дорівнюють одна одній. Знайдіть довжини рівних сторін.
1199. Накресліть прямокутник зі сторонами 6 см і 2 см. Побудуйте квадрат, периметр якого дорівнює периметру цього прямокутника. Обчисліть площі прямокутника і квадрата.
1200. Квадрат зі стороною 1 м поділили на чотири рівні частини і провели діагональ (рис. 216). Чому дорівнює площа заштрихованої фігури?
1201. Периметр квадрата дорівнює 11,2 см. Знайдіть периметр прямокутника, площа якого дорівнює площі даного квадрата, а одна із сторін – 9,8 см.
1202. Довжина прямокутника дорівнює 45 см. На скільки квадратних сантиметрів зменшиться площа цього прямокутника, якщо його ширина зменшиться на 4 см?
1203. Ребро одного куба в 3 рази більше за ребро другого. У скільки разів об’єм першого куба більший за об’єм другого?
1204. Об’єм прямокутного паралелепіпеда дорівнює 320 см3. Кожний вимір цього паралелепіпеда зменшили у 2 рази. Знайдіть об’єм утвореного паралелепіпеда.
1205. Довжина прямокутного паралелепіпеда дорівнює 12 см, ширина – 5 см, висота – 9 см. На скільки збільшиться об’єм паралелепіпеда, якщо кожний його вимір збільшити на 1 см?
1206. Довжина прямокутного паралелепіпеда дорівнює 36 см, ширина становить 
його довжини. Обчисліть об’єм паралелепіпеда, якщо його ширина становить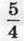 
висоти.
1207. Ширина прямокутного паралелепіпеда дорівнює 42 см, що становить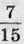 
його довжини, а висота становить 
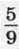довжини. Знайдіть об’єм паралелепіпеда і виразіть його в кубічних дециметрах.
1208. Прямолінійна ділянка шосе проходить через села Вишневе, Яблуневе і Грушеве. Відстань між селами Вишневе і Яблуневе дорівнює 3,2 км, що в 1,5 раза менше, ніж відстань між селами Яблуневе і Грушеве. Знайдіть відстань між селами Вишневе і Грушеве. Скільки розв’язків має задача?
1209. У басейн, що має форму прямокутного паралелепіпеда, щосекунди наливається 0,8 л води. Водночас через другу трубу з нього щосекунди виливається 0,75 л. Довжина басейну дорівнює 4,05 м, ширина – 120 см, глибина – 75 см. За скільки годин наповниться басейн?
1210. У двох мішках було 82,3 кг яблук, причому в одному мішку було на 7,9 кг яблук більше, ніж у другому. Скільки кілограмів яблук було в кожному мішку?
1211. За 2 год турист пройшов 9,6 км, причому за першу годину він пройшов на 1,2 км менше, ніж за другу. Знайдіть, яку відстань проходив турист за кожну годину.
1212. Олеся та Оленка зібрали 17,6 кг груш, причому Олеся зібрала на 2,7 кг більше, ніж Оленка. Скільки кілограмів груш зібрала кожна дівчинка?
1213. Крокодил Гена з’їв у 4 рази більше морозива, ніж Чебурашка. Скільки кілограмів морозива з’їв кожний із них, якщо Чебурашка з’їв на 2,4 кг менше, ніж крокодил Гена?
1214. За два дні подорожі велотуристи подолали 126 км, причому за другий день вони проїхали у 3,5 раза більше, ніж за перший. Знайдіть, скільки кілометрів вони проїжджали кожного дня.
1215. Зореліт “Сиріус” пролітає за 1 с на 650 км більше, ніж зореліт “Арктур”. Знайдіть швидкість кожного зорельота (у кілометрах за секунду), якщо швидкість “Арктура” у 2,3 раза менша від швидкості “Сиріуса”.
1216. Ніф-Ніф, Нуф-Нуф і Наф-Наф купили будівельні матеріали для ремонту своїх домівок, витративши на їх придбання 740 грн. Знайдіть витрати кожного поросяти, якщо Ніф-Ніф заплатив на 64,3 грн, а Нуф-Нуф на 32,5 грн більше, ніж Наф-Наф.
1217. За три дні продали 280 кг помідорів, причому за перший день продали у 2,8 раза менше, ніж за другий, і в 4,2 раза менше, ніж за третій. Скільки кілограмів помідорів продали за кожний із днів?
1218. Два автомобілі виїхали одночасно назустріч один одному з двох міст, відстань між якими дорівнює 360 км. Через 2,4 год після початку руху вони ще не зустрілися і відстань між ними становила 24 км. Знайдіть швидкість кожного автомобіля, якщо швидкість одного з них на 10 км/год більша за швидкість другого.
1219. Власна швидкість човна у 8 разів більша за швидкість течії річки. Знайдіть швидкість течії і власну швидкість човна, якщо: 1) за 5 год руху проти течії річки човен проплив 42 км; 2) за 4 год руху за течією річки човен проплив 50,4 км.
1220. Сума довжини і ширини прямокутника дорівнює 12 дм, причому ширина на 3,2 дм менша від довжини. Обчисліть площу прямокутника.
1221. Якщо в деякому десятковому дробі перенести кому вліво через дві цифри, то він зменшиться на 158,4. Знайдіть цей дріб.
1222. Скільки існує двоцифрових чисел, у яких перша цифра на 3 більша за другу?
1223. Розгадайте кросворд:
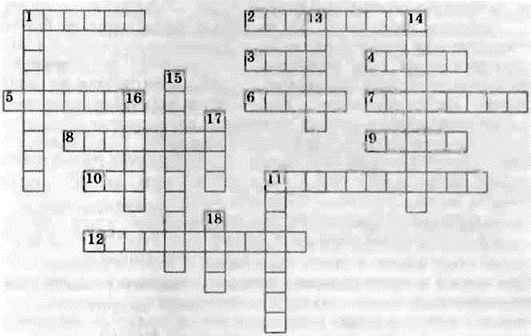
По горизонталі: 1. Компонент дії ділення. 2. Вид многокутника. 3. Одиниця довжини. 4. Одна з відомих вам величин. 5. Прямокутник, у якого всі сторони рівні. 6. 1000 кілограмів. 7. Геометрична фігура. 8.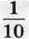 
метра. 9. Знак арифметичної дії. 10. Фігура, утворена двома променями зі спільним початком. 11. Вид чотирикутника. 12. Прилад для вимірювання кутів.
По вертикалі: 1. Арифметична дія. 11. Сума довжин сторін многокутника. 13. Розв’язок рівняння. 14. Число, яке визначає положення точки на координатному промені. 15. Промінь, що ділить кут навпіл. 16. Трицифрове число. 17.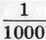 
кілограма. 18. Знак, що розділяє цілу і дробову частини десяткового дробу.
Дружимо з комп’ютером
Ви, звісно, знаєте, що сучасні комп’ютери стали надійними помічниками людей у багатьох видах діяльності. І в опануванні математики комп’ютер також допоможе вам. Ви зможете:
– користуватися калькулятором для обчислень;
– набирати й оформляти нескладні тексти в текстовому редакторі (наприклад, у Microsoft Word);
– складати таблиці за допомогою редактора таблиць (наприклад, у Microsoft Excel);
– користуватися глобальною мережею Інтернет і шукати в ній інформацію;
– зображати геометричні фігури тощо.
Звернемо увагу на те, що на уроках математики ви будете створювати не художні малюнки, а креслення та схеми. У стандартному графічному редакторі, призначеному для створення художніх малюнків (наприклад, у Paint), це робити не дуже зручно і досить трудомістко. Тому корисно навчитися працювати з графічним редактором, за допомогою якого можна оперувати геометричними фігурами та будувати креслення. Прикладами таких редакторів можуть бути редактор рисунків, убудований в текстовий редактор Microsoft Word, а також CorelDraw, Visio тощо. Оберіть разом з учителем графічний редактор, яким ви зможете користуватися та створювати рисунки до завдань цього розділу.
Ви можете виконувати деякі вправи цього підручника за допомогою комп’ютера. У тексті підручника їх помічено знаком. Для кожної з таких вправ тут наведено додаткове завдання, яке виконується за допомогою комп’ютера (поряд указано номер відповідної вправи з тексту підручника або, якщо вправа відповідає теоретичній частині пункту, – номер цього пункту).
П. 1. Натуральні числа використовують для нумерації об’єктів. Автори багатьох програм, якими ви будете користуватися, прагнуть полегшити людям роботу, створюючи засоби автоматичної нумерації різних списків.
1) Знайдіть у редакторі Word засіб, який дає змогу пронумерувати список числами з натурального ряду. Створіть кілька списків і виконайте їх автоматичну нумерацію.
2) Якими ще програмами ви користуєтесь? Чи є в них корисні
Інструменти, які також використовують властивості натурального ряду?
13. Перевірте виконання цього завдання за допомогою калькулятора, зверніть увагу на порядок виконання дій.
36. Перевірте результат своїх обчислень за допомогою калькулятора.
38. Знайдіть в Інтернеті історичні відомості про опанування космосу. Хто з космонавтів походить з України?
41. Знайдіть в Інтернеті інформацію про перші літаки та вертольоти. Хто був конструктором першого у світі вертольоту?
П. 3. 1) Навчіться зображати відрізки й точки у графічному редакторі.
2) Чи можна зобразити на папері або на екрані комп’ютера точку “в натуральну величину”? Як доводиться зображати точки, щоб їх було добре видно на рисунку?
3) Нарисуйте на екрані відрізок. Збільште зображення до максимально можливого розміру. Які недоліки має це зображення з точки зору математики?
47-50. 1) Знайдіть у графічному редакторі інструмент, який інформує про довжину зображеного відрізка. Як використовувати цей інструмент для виконання завдань 47-50?
2) Виконайте які-небудь із завдань 47-50 за допомогою графічного редактора. Підпишіть буквами кінці нарисованого відрізка та зображені точки.
51. Ця задача присвячена відомій зоровій ілюзії. Попа демонструє, що залежно від оформлення кінців відрізка його довжина сприймається більшою або меншою. Знайдіть в Інтернеті інформацію про такі зорові ілюзії, наведіть інші цікаві приклади зорових ілюзій.
80. Знайдіть в Інтернеті інформацію про Василя Олександровича Сухомлинського. Якими педагогічними здобутками набув відомості цей учитель?
“Від ліктів та долонь – до метричної системи”. На які ще одиниці виміру довжини ви натрапляли в художній літературі? Знайдіть в Інтернеті міри довжини, що використовувались у різних країнах за різних часів, і складіть таблицю, якою ви зможете користуватися під час читання.
86. Виконайте це завдання за допомогою графічного редактора. Чи можна зобразити на папері або на екрані комп’ютера пряму “в натуральну величину”? У який спосіб доводиться зображати прямі? Які особливості потрібно врахувати, проводячи пряму через точку на екрані комп’ютера? (Якщо вам складно відповісти на це запитання, то нарисуйте точку та пряму і збільште це зображення до максимально можливого розміру.)
П. 5. Відкрийте текстовий редактор; графічний редактор. Чи є на екрані які-небудь шкали? Що вони позначають? Яка ціна поділки шкали?
119. Виконайте це завдання за допомогою графічного редактора. За зразок для зображення координатного променя можна взяти рисунок 51. Збережіть файл із зображенням координатного променя, він стане в нагоді для виконання наступних завдань.
141. Чи знаєте ви, яка найвища історична будівля в Києві? у Львові? Знайдіть в Інтернеті інформацію про знамениті архітектурні споруди цих міст або міст вашого регіону та складіть аналогічну задачу.
166. Знайдіть в Інтернеті інформацію про найстаріші навчальні заклади, розташовані на території сучасної України. У якому столітті був заснований кожний із них? Яких наук навчали в них студентів?
169. Перевірте результати своїх обчислень за допомогою калькулятора.
181. Знайдіть в Інтернеті розклад руху поїздів на якій-небудь станції Укрзалізниці. Користуючись ним, складіть аналогічну задачу, у якій запитується, скільки часу поїзд буде в дорозі.
201. Перевірте результати своїх обчислень за допомогою калькулятора.
204. До таблиці, наведеної в цьому завданні, включено не всі планети Сонячної системи. Користуючись Інтернетом, знайдіть назви решти планет і максимальні відстані від них до Сонця, (складіть таблицю в табличному редакторі. Упорядкуйте таблицю так, щоб планети були розміщені за зростанням їх відстаней від Сонця. Які ще цікаві числові відомості про ці планеті! можна включити до таблиці?
208. Знайдіть в Інтернеті інформацію про площі територій європейських країн. Складіть у текстовому редакторі таблицю, яка містить відомості про площі територій п’яти найбільших країн Європи.
238. У якому році ви читаєте цей підручник? Скільки Міжнародних математичних олімпіад відбулося з того часу як було надруковано цей підручник? Знайдіть в Інтернеті інформацію про виступи української команди за ці роки та доповніть таблицю, наведену в підручнику.
П. 9. Коли ви починаєте записувати алгоритми та знайомитеся з деякою мовою програмування, то дізнаєтеся про те, як записують змінні. Що означає запис mn у математиці і в програмуванні? Чи має сенс запис у4? Зробіть висновок щодо вживання знака множення в математиці і в інформатиці.
258. Перевірте обчислення за допомогою калькулятора.
277. Чи знаєте ви, за мотивами якої казки О. М. Толстой написав “Пригоди Буратіно”? Хто був автором тієї казки? У якій країні жив письменник і герої його казки? Знайдіть в Інтернеті інформацію про те, яку валюту використовують у цій країні в наш час.
297. У яких Олімпійських іграх уперше брала участь команда незалежної України? Скільки медалей вона виборола і яких? Знайдіть ці дані за допомогою Інтернету й складіть аналогічну задачу.
300. Виконайте це завдання за допомогою графічного редактора. Чи є в цьому графічному редакторі інструмент, який дає змогу визначати величину кута?
П. 13. Нарисуйте за допомогою графічного редактора довільний многокутник. Які засоби графічного редактора дають змогу зобразити фігуру, рівну вже нарисованій?
338. Перевірте обчислення за допомогою калькулятора.
340. Перевірте правильність своєї відповіді, знайшовши в Інтернеті інформацію про висоти цих гір. Складіть за допомогою табличного редактора таблицю, яка містить інформацію про п’ять найвищих гір України. Інформацію, якої бракує, знайдіть в Інтернеті. Упорядкуйте інформацію за зменшенням висоти гір. Яку ще цікаву інформацію можна включити до цієї таблиці? Користуючись Інтернетом, складіть аналогічну задачу про інші географічні об’єкти України.
343, 344. Нарисуйте шукані трикутники за допомогою графічного редактора. Якими інструментами графічного редактора ви скористаєтесь, щоб переконатися, що нарисований трикутник дійсно має потрібні властивості?
393. Перевірте результат своїх обчисліть за допомогою калькулятора.
П. 17.* У цьому пункті ви бачили багато прикладів того, що в записах дії множення немає знака множення. Спробуйте скласти алгоритм, який визначає, коли потрібно писати знак множення при записі виразу.
454. Створіть цю таблицю в табличному редакторі. Чи можете ви зробити так, щоб значення в порожніх клітинках обчислювались автоматично?
471. Запишіть формулу, що містить змінну “витрати палива на 100 км шляху” та дає змогу обчислити відстань, яку можна проїхати, використавши 1 л палива.
Знайдіть в Інтернеті інформацію про витрати палива кількох марок легкових автомобілів. Складіть у табличному редакторі таблицю:
Марка автомобіля | Витрати палива на 100 км шляху | Відстань, яку можна проїхати, використавши 1 л палива |
Задайте відстань за допомогою формули й зробіть так, щоб вона підраховувалась автоматично на підставі графи “Витрати палива на 100 км шляху”.
481. Які одиниці довжини та які одиниці маси використовувались у Франції за часів д’Артаньяна? Чому вони дорівнюють у перерахунку на одиниці сучасної метричної системи мір?
Які грошові одиниці використовувались у той час і як вони співвідносилися між собою? Знайдіть в Інтернеті цю інформацію та складіть таблицю, якою ви зможете користуватися під час читання книг про пригоди мушкетерів.
482. Для вимірювання швидкості моряки використовують спеціальну одиницю виміру, що дорівнює одній милі за годину. Знайдіть в Інтернеті, як її називають. У яких книгах ви з нею стикалися? Поцікавтеся біографічними відомостями про авторів цих книг.
564. Обчисліть значення складених виразів за допомогою калькулятора. Зверніть увагу на те, як у даному калькуляторі потрібно задавити порядок дій. Дослідіть відмінність між “звичайним* та “інженерним” режимами стандартного калькулятора Windows.
П. 21. Що таке акр? Де ви можете почути або прочитати це слово? Під час вивчення одиниць довжини ви складали таблицю мір довжини, які використовувалися в різних країнах за різних часів. Доповніть цю таблицю мірами площі та інформацією про співвідношення мір, які використовувалися в одній країні. Чи можете ви знайти відомості про те, звідки походять ці міри? Які поняття з повсякденного життя брали до уваги, обираючи “одиничну” міру?
582. Чи видумував Джонатан Свіфт у книзі про мандри Гуллівера спеціальні одиниці виміру для ліліпутів і велетнів? Якщо ні, то придумайте такі одиниці. Складіть у табличному редакторі таблицю переведення цих одиниць у метричну систему. Складіть задачу з використанням таких одиниць виміру.
586. Розв’язуючи цю задачу, виконайте обчислення за допомогою калькулятора.
П. 22. Зверніть увагу на зображення паралелепіпеда і піраміди на рисунках цього пункту. Чому використано різні типи ліній? Навчіться задавати потрібний тип лінії в графічному редакторі. Нарисуйте довільну піраміду.
П. 23. Які міри площі, об’єму використовувались у Стародавній Русі? на території України в середні віки?
638. Перевірте результати своїх обчислень за допомогою калькулятора.
П. 24. Поміркуйте, як зручніше використовувати табличний редактор для запису всіх можливих варіантів під час розв’язування комбінаторних задач. Використайте ці засоби для розв’язування кількох задач цього пункту на ваш вибір.
693. Знайдіть в Інтернеті числові дані щодо географічних об’єктів України та складіть аналогічні задачі на дроби.
696. Виконайте це завдання за допомогою графічного редактора.
З яких міркувань ви оберете розмір зображення одиничного відрізка на екрані?
763. Спробуйте підрахувати значення записаної частки за допомогою калькулятора, і ви зрозумієте, чому калькулятор може стати в нагоді далеко не у всіх випадках, п. 29. Чи можна за допомогою калькулятора визначити, що дане натуральне число ділиться націло на інше? Як ви це робитимете й коли будете впевнені у своїй відповіді?
Шукаючи відповідь на попереднє запитання, ви, мабуть, переконалися, що калькулятор точно знаходить цілу частину шуканого мішаного числа. Як, користуючись цим, знайти чисельник дробової частини?
Запишіть алгоритм для перетворення неправильного дробу в мішане число з використанням калькулятора.
816. Виконайте це завдання за допомогою графічного редактора, п. 33. Навчіться додавати і віднімати десяткові дроби за допомогою калькулятора. Зверніть увагу на те, як потрібно вводити кому. Виконайте кілька завдані, цього пункту на ваш вибір за допомогою калькулятора.
885. Знайдіть в Інтернеті цікаву інформацію про частини світу й складіть аналогічну задачу.
886. Знайдіть в Інтернеті інформацію про водойми України. За допомогою знайденої інформації винесіть зміни н умови задачі, щоб у ній ішлося про українські водойми.
П. 34. Навчіться множити десяткові дроби за допомогою калькулятора. Виконайте кілька завдань цього пункту на ваш вибір за допомогою калькулятора.
938, 939. 1) До складу яких держав входили різні області України протягом певних періодів? Які одиниці виміру використовувались у цих державах, а отже, і на території України? Знайдіть цю інформацію в Інтернеті.
2) Складіть у табличному редакторі таблицю для переведення старовинних одиниць довжини в сучасну метричну систему. Якого вигляду треба надати таблиці, щоб включити до неї інформацію і про часи, у які використовувалось та чи інша одиниця?
3) Складіть у табличному редакторі таблицю для переведення старовинних одиниць маси в сучасну метричну систему. Оформіть цю таблицю і таблицю з одиницями довжини як дві сторінки одного й того самого файлу.
4) Знайдіть біографічні відомості про інженерів та науковців різних часів, які народилися на території сучасної України, та оформіть їх у текстовому редакторі з включенням до нього ілюстрацій. Кожний учень вашого класу може обрати для виконання цього завдання представників різних галузей науки і техніки, які працювали в різні періоди та були громадянами різних держав.
Таблиці, які ви створили, стануть у нагоді під час читання історичних книг.
П. 35. Навчіться ділити десяткові дроби за допомогою калькулятора. Виконайте кілька завдань цього пункту на ваш вибір за допомогою калькулятора.
П. 36. 1) Створіть у табличному редакторі таблицю, до якої щоденно протягом трьох тижнів будете заносити величини своїх витрат. Підрахуйте середнє арифметичне для робочих днів тижня; для вихідних днів; за весь тиждень. Як можна автоматизувати процес обчислення середнього арифметичного?
2) Знайдіть в Інтернеті інформацію про площі трьох найбільших прісноводних природних водойм (озер) України і про площі трьох найбільших штучних водойм (водосховищ). Обчисліть середнє арифметичне для кожного із цих типів водойм. Зробіть висновки про те, який тип водойм має більшу середню площу. Чи зміниться відповідь, якщо розглянути більшу кількість водойм?
3) Знайдіть в Інтернеті інформацію про потужність кількох найбільших українських електростанцій різного типу (гідроелектростанцій, теплових, атомних). Складіть таблицю. Визначте середню потужність станцій залежно від їх типу. Знайдіть інформацію про розвиток у світі електростанцій, що працюють на альтернативних джерелах енергії (Сонця, припливів, вітру). Яку таблицю можна скласти, щоб отримати цікавий матеріал для порівняння?
4) Знайдіть в Інтернеті інформацію про витрати природних ресурсів та енергії під час вироблення паперу з деревини та з макулатури.
1041. 1) Обчисліть свою середню оцінку з математики за II чверть.
2) Визначте середню оцінку учнів вашого класу з математики за II чверть. Як можна скористатися знайденими середніми оцінками кожного учня, щоб якнайшвидше виконати це завдання? Спробуйте виконати це завдання за допомогою табличного редактора.
1064. Знайдіть в Інтернеті цікаву інформацію про населення України. Яку інформацію зручно подати з використанням відсотків?
1075. Знайдіть в Інтернеті, яка концентрація солі: 1) у середньому у Світовому океані; 2) у найсолонішій водоймі світу, Мертвому морі (Ізраїль). Обчисліть за допомогою калькулятора, скільки солі міститься у 250 кг води Мертвого моря.
1109. Розв’язуючи цю задачу, виконайте обчислення за допомогою калькулятора.
(1 votes, average: 5.00 out of 5)
Loading...