Головна ⇒ 📌Математика ⇒ Знаходження дробу від числа

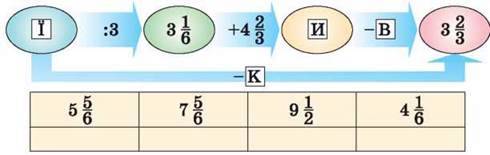
Знаходження дробу від числа

Розділ 2 Звичайні дроби

§15. Знаходження дробу від числа

Розглянемо задачу, що зводиться до знаходження дробу від числа.

Задача 1. У класі 30 учнів, 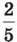із них хлопці. Скільки хлопців у класі?

Розв’язання. (Мал. 3).

1) 30 : 5 = 6 (уч.) – становить 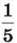від 30 учнів;

2) 6 ∙ 2 = 12 (уч.) – становить 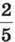від 30 учнів.

Отже, у класі 12 хлопців.

Розв’язання цієї задачі можна записати інакше:

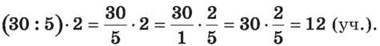
Отже, кількість хлопців у класі можна знайти,

якщо помножити кількість усіх учнів (30) на дріб

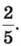При розв’язуванні задачі знайшли дріб

від числа 30.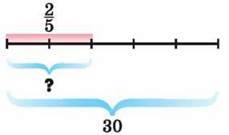

Мал. 3

Задачі на знаходження дробу від числа розв’язують дією множення.

– Щоб знайти дріб від числа, достатньо число помножити на цей дріб.

Задача 2. Ширина прямокутника дорівнює 12 см, а довжина становить ширини. Знайти довжину прямокутника.

Розв’язання. Довжина прямокутника дорівнює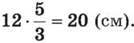

Задача 3. У книжці 140 сторінок. Першого дня учень прочитав 0,3 від усієї кількості

сторінок. Скільки сторінок прочитав учень першого дня?

Розв’язання. Оскільки 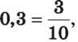то для розв’язання задачі треба помножити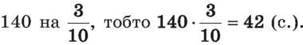

Отже, першого дня учень прочитав 42 сторінки. Той самий результат отримаємо, якщо помножити 140 на 0,3: 140 ∙ 0,3 = 42.

Розглянемо як можна застосувати це правило для знаходження відсотків від числа.

Задача 4. Турист повинен пройти 12 км. За першу годину він пройшов 25 % цієї відстані. Скільки кілометрів пройшов турист за першу годину?

Розв’язання. Запишемо 25 % десятковим і звичайним дробом: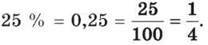

Помножимо дане число на цей дріб: 12 ∙ 0,25 = 3, або 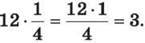Отже, за першу годину турист пройшов 3 км. Сформулюй правило знаходження дробу від числа. і Як знайти відсотки від числа?

343. (Усно) Знайди:

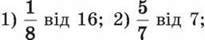
3) 0,4 від 100; 4) 30 % від 40.

344. Обчисли:

3) 0,7 від 40; 4) 0,32 від 10;

5) 10 % від 27; 6) 20 % від 30.

345. Обчисли:

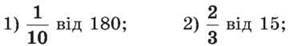3) 0,5 від 10;

4) 0,47 від 100; 5) 50 % від 2; 6) 30 % від 40.

346. Петро зібрав 40 грибів, з яких 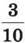– маслюки. Скільки маслюків зібрав Петро?

347. Маса бегемота 2000 кг, а маса носорога становить 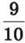маси бегемота. Знайди масу носорога.

348. Площа однієї кімнати 21 м2, а площа другої становить від площі першої кімнати. Знайди площу обох кімнат разом.

349. Поштарка має доставити адресатам 96 листів, причому 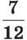кількості листів вона доставила до обіду. Скільки листів залишилося поштарці доставити адресатам?

350. Дві бригади трактористів зорали 550 га землі, при чому перша бригада виконала 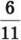цього обсягу. Скільки гектарів землі зорала друга бригада? 351. Запиши звичайним дробом:

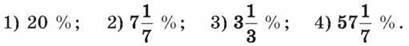
Розв’язання. 4) Оскільки 1% = 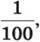то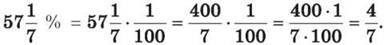

352. Запиши у вигляді відсотків дріб:

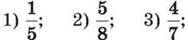4) 0,215; 5) 2,7; 6) 4,19.

Розв’язання. 3) Оскільки 1 = 100 %, то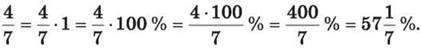

353. Запиши:

1) звичайним дробом: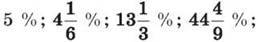

2) у вигляді відсотків: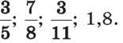

354. Довжина прямокутника 24 см, а ширина становить 75 % довжини. Знайди площу прямокутника.

355. Довжина прямокутника 25 см, а ширина становить довжини. Обчисли периметр прямокутника.

356. Знайко прочитав книжки, яка має а сторінок. Склади вираз для знаходження кількості сторінок, які прочитав Знайко, та знайди його значення, якщо а = 180.

357. Знайди:

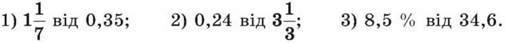
358. Знайди:

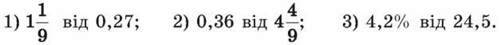
359. Морська вода містить 7 % солі. Скільки солі міститься в 340 кг морської води?

360. Токар мав виготовити за день 200 деталей. Але він перевиконав завдання на 5 %. Скільки деталей виготовив токар?

361. На базу привезли 2800 кг картоплі. З них 45 % привезли першого дня, а решту – другого. Скільки кілограмів картоплі привезли першого дня і скільки другого?

362. Під час сушіння яблука втрачають 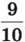своєї маси. Скільки кілограмів сушених яблук вийде з 240 кг свіжих?

363. За три дні зібрали 532 кг насіння соняшника. У перший день зібрали 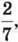у другий – 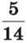цієї маси. Скільки кілограмів насіння було зібрано в третій день?

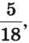364. Три кондитери виготовили 270 тортів. Перший виконав цієї роботи, другий – а третій – решту. По скільки тортів виготовив кожен кондитер?

365. На базі було 270 ц картоплі. Спочатку вивезли від цієї маси, а потім – 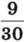від того, що залишилося. Скільки центнерів картоплі після цього залишилося на базі?

366. Від стрічки довжиною 40 м спочатку відрізали 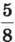її довжини, а потім – 0,45 решти. Скільки метрів стрічки відрізали за другий раз?

367. Автомобіль за 3 год проїхав 234 км. За першу годину він проїхав 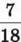цієї відстані, за другу – 0,4 решти. Яку відстань проїхав автомобіль за третю годину?

368. Що більше: 18,7 % від 12,7 чи 12,7 % від 18,7?

369. Яке із чисел x або у є більшим (х та у не дорівнюють нулю), якщо:

370. Розв’яжи рівняння і виконай перевірку:

1) 3x = 1; 2) x ∙ 13 = 1; 3) 0,2x = 1.

371. Використовуючи цифри 0, 1, 2, 3, 5, запиши найбільше та найменше трицифрові числа, кратні числу 3 так, щоб цифри в кожному числі не повторювалися.

372. Знайди невідомі числа та склади назву столиці європейської держави.