Аналітичні способи розв’язування систем лінійних рівнянь із двома змінними
Розв’яжіть задачі
1121. 1) х = 2y + 3; 2); х = -3у – 9; 3) х = 2у – 2,5; 4) х = 2y – 3.
1122. 1) у = 15 – 5х; 2) у = 4х + 6; 3) у = 6 – 2х; 4) у = 2 + 1,5х.
1123. 1) 2y – 2y = 3; 0 ≠ 3; немає розв’язку;
2) 3 • (2y) + 3y = 9; 6y + 3у – 9; 9y = 9; у = 1;
3) 4y + у = 5; у = 1;
4) 4у – 4у = 0; 0 ≠ 5; немає розв’язку.
1124. 1) 5х + 5х = 30; 10x = 30; х = 3;
2) 4x – 5х = 6; – х = 6; х = -6;
3) 3х + 10x = 13; 13x = 13; х = 1;
4) 10х – 20х = 5; -10х = 5; х = -1/2.
1125. 1) Ні; 2) так.
1126. 1) Так; 2) ні.
1127. 1) 3 і -2; 2) -4 і 3.
1128. 1) Ні; 2) так.
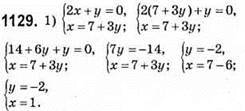
Відповідь: (1; -2).
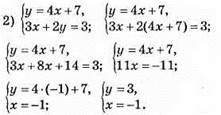
Відповідь:
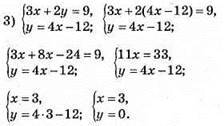
Відповідь: (3; 0).
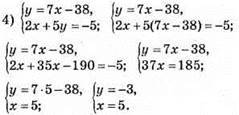
Відповідь: (5; -3).
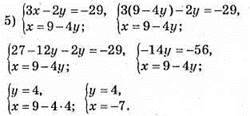
Відповідь: (-7; 4).
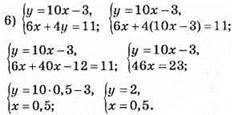
Відповідь: (0,5; 2).
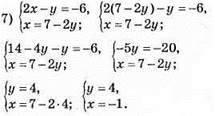
Відповідь: (-1; 4).
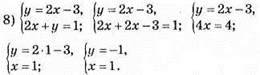
Відповідь: (1; -1).
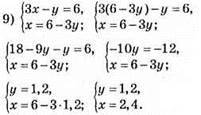
Відповідь: (2,4; 12).
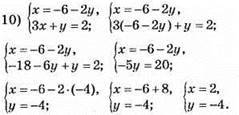
Відповідь: (2; -4).
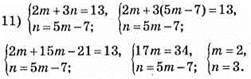
Відповідь: (2; 3).
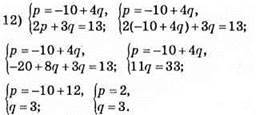
Відповідь: (2; 3).
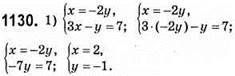
Відповідь: (2; -1).
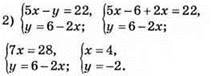
Відповідь: (4; -2).
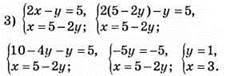
Відповідь:
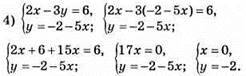
Відповідь: (0; -2)
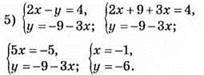
Відповідь: (-1; -6).
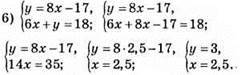
Відповідь: (2,5; 3).
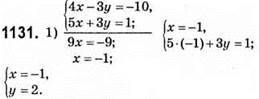
Відповідь: (-1; 2).
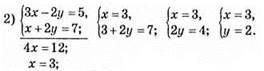
Відповідь: (3; 2).
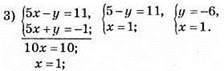
Відповідь: (1; -6).
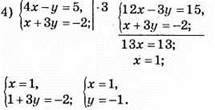
Відповідь: (1; -1).
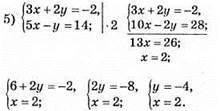
Відповідь: (2; -4).
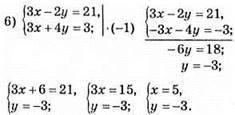
Відповідь: (5; -3).
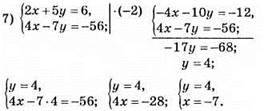
Відповідь: (-7; 4).
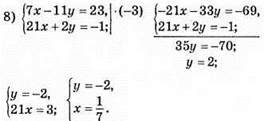
Відповідь: (1/7; -2).
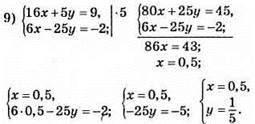
Відповідь: (0,5; 1/5).
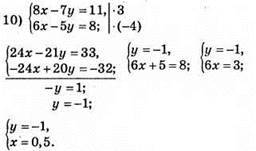
Відповідь: (0,5; -1).
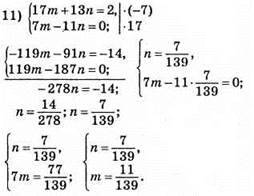
Відповідь: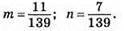 
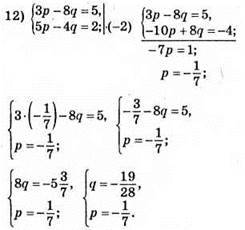
Відповідь: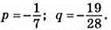 
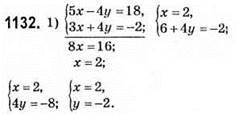
Відповідь: (2; -2).
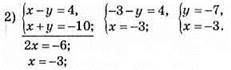
Відповідь: (-3; -7).
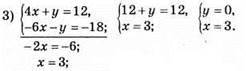
Відповідь: (3; 0).
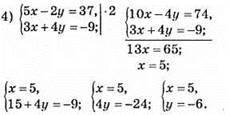
Відповідь: (5; -6).
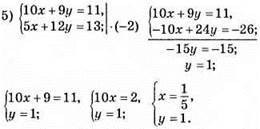
Відповідь: (1/5; 1).
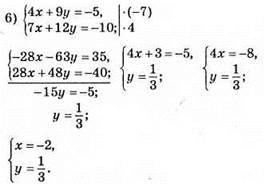
Відповідь: (-2; 1/3).
1133. 1) Спосіб підстановки:
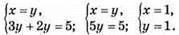
Відповідь: (1; 1).
2) Спосіб додавання:
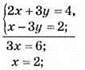
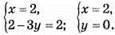
Відповідь: (2; 0).
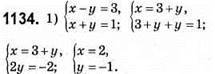
Відповідь: (2; -1).
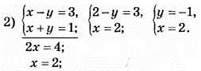
Відповідь: (2; -1).
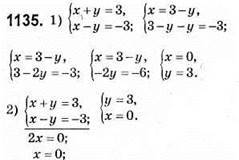
1136. Нехай числа х і у.
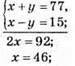
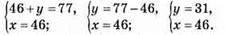
Відповідь: числа 31 і 46.
1137. Нехай числа х і у, тоді
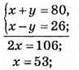
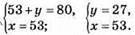
Відповідь: числа 27 і 53.
1138. Нехай числа х і у, тоді
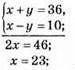
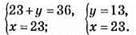
Відповідь: (23; 13), числа 23 і 13.
1139. Нехай числа х і у, тоді
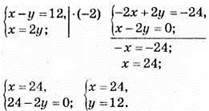
Відповідь: числа 12 і 24.
1140. Нехай шукані числа х і у, тоді
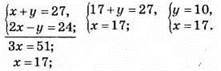
Відповідь: числа 10 і 17.
1141. Нехай числа х і y, тоді
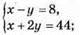
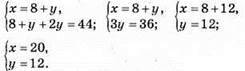
Відповідь: числа 12 і 20.
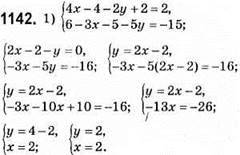
Відповідь: (2; 2).
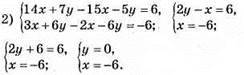
Відповідь: (-6; 0).
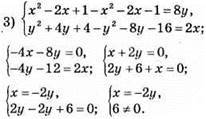
Відповідь: система не має розв’язку.
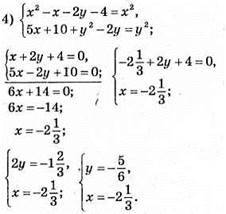
Відповідь: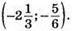 
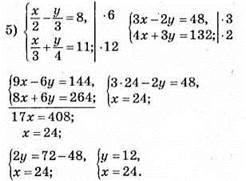
Відповідь: (24; 12).
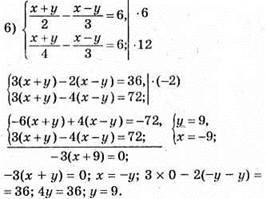
Відповідь: (-9; 9).
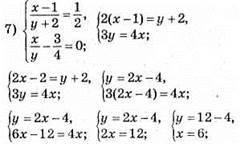
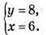
Відповідь: (6; 8).
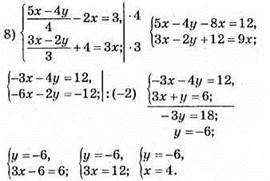
Відповідь: (4; -6).
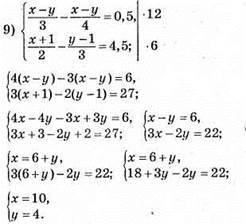
Відповідь: (10; 4).
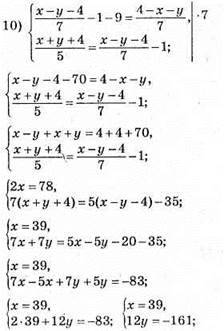
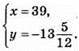
Відповідь: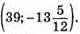 
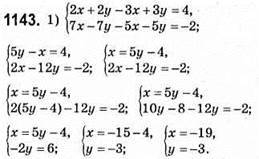
Відповідь: (-19; -3).
Відповідь: (1; -1,5).
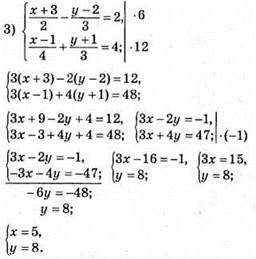
Відповідь: (5; 8).
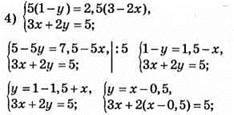
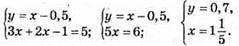
Відповідь: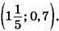 
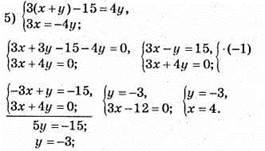
Відповідь: (4; -3).
1144. Нехай у першому кошику х яблук, а у другому у яблук, складаємо систему за умовою задачі:
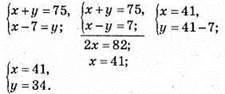
У першому кошику 41 яблуко, а у другому – 34 яблука.
1145. Нехай на першій полиці х книжок, а на другій – у книжок. Разом х + у = 40, складаємо систему рівнянь:
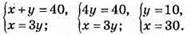
На полицях стоїть 10 і 30 книжок.
1146. Нехай ширина прямокутника х, тоді довжина у, маємо систему:
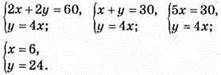
Сторони прямокутника 6 см і 24 см.
1147. Нехай сторони прямокутника х см і у см, тоді
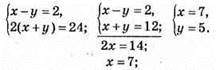
Сторони прямокутника 5 см і 7 см.
1148. Нехай 1 кг печива коштує х грн, а 1 кг цукерок – у грн, маємо:
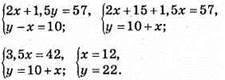
1 кг печива коштує 12 грн, a 1 кг цукерок коштує 22 грн.
1149. Нехай 1 кг груш коштує х грн, а 1 кг яблук – у грн, маємо:
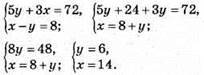
1 кг груш коштує 14 грн, а 1 кг яблук – 6 грн.
1150. Нехай швидкість поїзда х км/год, а швидкість автобуса у км/год. Складаємо систему рівнянь за умовою задачі:
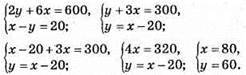
Швидкість поїзда дорівнює 80 км/год.
1151. Нехай швидкість руху на автомобілі х км/год, а швидкість руху пішки – у км/год. Складаємо систему за умовою:
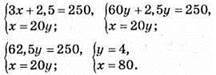
Швидкість руху на автомобілі була 80 км/год.
1152. Нехай швидкість 1-го велосипедиста х км/год, а другого – у км/год, тоді
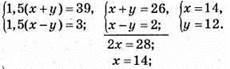
Швидкість велосипедистів – 12 км/год і 14 км/год.
1153. Нехай швидкість першого автобуса була х км/год, а швидкість другого – y км/год, тоді:
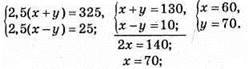
Швидкість першого автобуса 70 км/год, а другого – 60 км/год.
1154. Нехай власна швидкість теплохода х км/год, а швидкість течії у км/год, маємо х + y – швидкість за течією, х – у – швидкість проти течії.
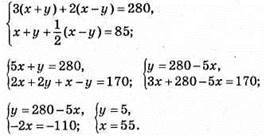
Власна швидкість теплохода – 55 км/ год, а швидкість течії – 5 км/год.
1155. Нехай власна швидкість човна х км/год, а швидкість течії річки – y км/год, х + y – швидкість за течією, x – y – швидкість проти течії.
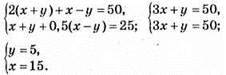
Власна швидкість човна 15 км/год, а швидкість течії – 5 км/год.
1156. Нехай за 1 год перший робітник виготовляє х деталей, а другий – у деталей.
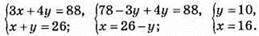
Перший робітник виготовив 48 деталей, а другий – 40 деталей.
1157. Нехай за 1 год один майстер пошив х костюмів, а другий – y костюмів.
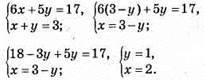
Перший майстер пошив 12 костюмів, а другий – 5 костюмів.
1158. Нехай у першому ящику х яблук, а у другому – y яблук, маємо:
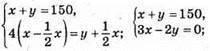
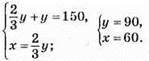
В ящиках було по 60 і 90 яблук.
1159. Нехай на першій полиці х книжок, а на другій – у. Складаємо систему за умовою задачі:
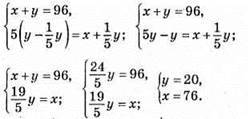
На першій полиці було 76 книжок, а на другій – 20 книжок.
1160. Нехай перше число х, друге – у.
Маємо:
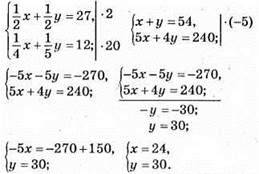
Відповідь: шукані числа 24 і 30.
1161. Нехай шукані числа х і у, тоді:
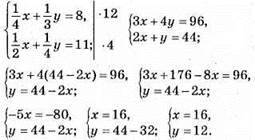
Відповідь: числа 16 і 12.
1162. Нехай спочатку в першій кімнаті було х осіб, а у другій – у осіб, тоді:
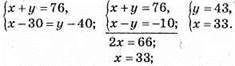
У першій кімнаті було 33 особи, а в другій – 43.
1163. Нехай на першій полиці х книжок, а на другій – y книжок, за умовою задачі:
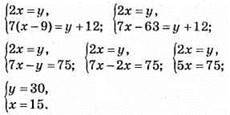
На полицях було 15 і 30 книжок.
1164. Нехай на першій полиці спочатку було х книжок, а на другій – у книжок, тоді за умовою задачі:
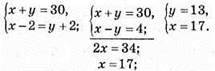
На полицях було 17 і 13 книжок.
1165. Нехай купець купив х аршин чорної тканини і у аршин синьої тканини. За умовою задачі складаємо систему:
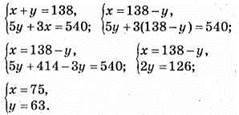
Купець купив 63 аршини синьої тканини і 75 аршин чорної тканини.
1166. Нехай у класі x дівчаток і у хлопчиків. Тоді носів у дівчаток x, а вух у хлопців 2у, і навпаки, носів у хлопців у, а вух у дівчаток 2x. Складаємо систему за умовою задачі:
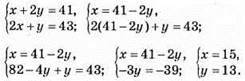
У класі 15 дівчат і 13 хлопців.
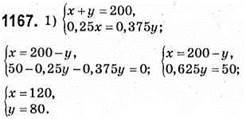
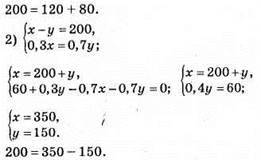
1168. Потрібно зменшити на 64. 100 – 64 = 36; 36: 5 = 7 (ост. 1); 36: 7 = 5 (ост. 1).
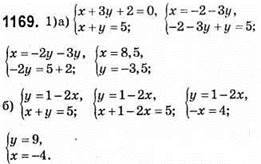
Відповідь: (-4; 9) або (8,5; -3,5).
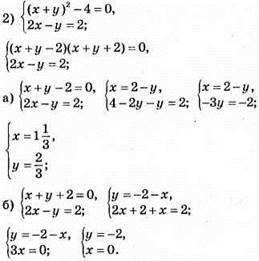
Відповідь: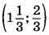 
або (0; -2).
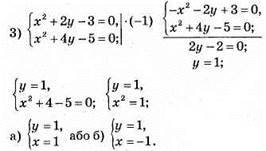
Відповідь: (1; 1) або (-1; 1).
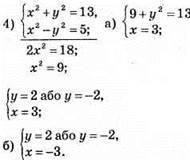
Відповідь: (-3; 2), (-3; -2), (3; 2), (3; -2).
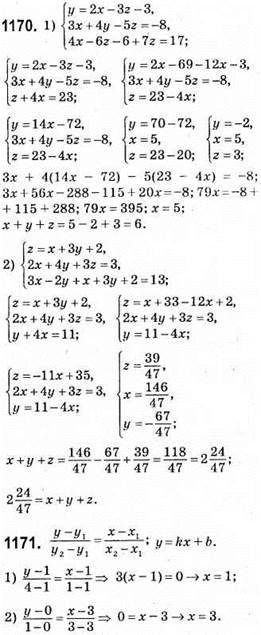
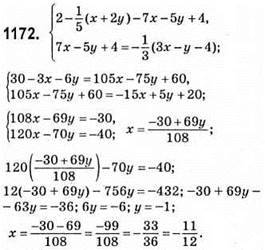
1173. 1) а ≠ 12; 2) а = 12.
1174. При с ≠ 3 система не має розв’язків.
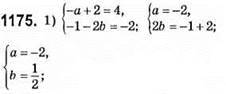
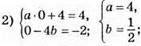а – будь-яке число.
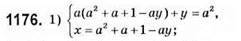
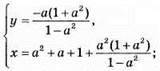при а ≠ ±1;
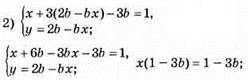
X = 1 при у = b, b ≠ 1/3.
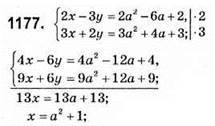
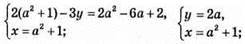
X + у = а2 + 2а + 1 = (а + 1)2 набуває найменшого значення при а + 1 = 0, тобто а = -1.
Застосуйте на практиці
1178. Нехай на турбазі x наметів і у будиночків, тоді
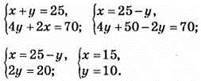
На базі 15 наметів і 10 будиночків.
1179. Нехай батькові x років, а синові у років, маємо систему:
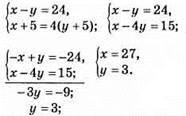
Батькові 27 років, а синові 3 роки.
1180. Нехай у класі x учнів, а вчитель приготував у аркушів для контрольної роботи. Складаємо систему за умовою задачі:
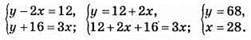
У класі 28 учнів, а вчитель приготував 68 аркушів.
1181. Нехай x – кролики, у – фазани.
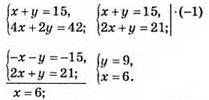
У клітці сиділо 6 кроликів і 9 фазанів.
Задачі на повторення
1182. 10% від 4000 грн = 4000 • 10 : 100 = 400 грн.
4000 + 400 = 4400 (грн) – заробітна плата після збільшення.
20 % від 4400 грн = 4400 • 20 : 100 = 880 грн.
4400 + 880 = 5280 (грн) – заробітна плата після збільшення на 20 % .
4000 грн – 100 %
5280 грн – х %
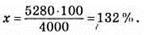
На (132 % – 100 %) = 32 % збільшилася заробітна платня токаря.
1183. Нехай на полиці було х книжок, тоді:
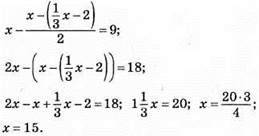
На полиці було 15 книжок.
(1 votes, average: 5.00 out of 5)
Loading...