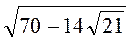Арифметичний квадратний корінь з добутку, дробу, степеня
Урок № 40
Тема. Арифметичний квадратний корінь з добутку, дробу, степеня
Мета: закріпити знання змісту властивостей арифметичного квадратного кореня з добутку, частки та степеня; відпрацювати вміння учнів застосовувати вивчені властивості для виконання обчислень значення числових виразів, що містять квадратний корінь, а також для перетворення виразів зі змінними.
Тип уроку: застосування знань та вмінь.
Наочність та обладнання: опорний конспект “Арифметичний квадратний корінь та його властивості”.
Хід уроку
I.
II. Перевірка домашнього завдання
Цей етап уроку проводимо у формі гри “Знайди помилку” (вчитель заздалегідь готує записи розв’язання домашніх вправ, допустивши в них помилки в контрольних моментах, наприклад не врахувавши знак, не змінивши степінь тощо).
III. Формулювання мети і завдань уроку
Основна мета уроку формулюється майже сама по собі після перевірки домашнього завдання: як показує досвід, дуже рідко учні засвоюють усі властивості арифметичного квадратного кореня відразу після їх безпосереднього вивчення (особливо це стосується вправ на застосування властивостей
Тому закріплення знань учнів про властивості арифметичного квадратного кореня та відпрацювання вмінь їх застосувати – висуваються як основне завдання на поточний урок.
IV. Актуалізація опорних знань та вмінь
@ З метою втілення в життя завдання, сформульоване на попередньому етапі уроку, слід активізувати такі знання і вміння учнів: означення і властивості арифметичного квадратного кореня з числа; властивості степеня раціональних чисел (парний степінь додатного та від’ємного чисел); розкладання натуральних чисел на прості множники.
Виконання усних вправ
1. Піднесіть до степеня: 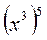 ;
; 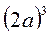 ;
; 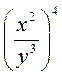 ;
; 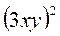 ;
; 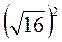 ;
; 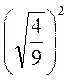 ;
; 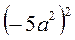 ;
; 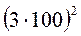 ;
; 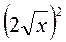 ;
; 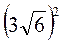 ;
; 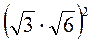 .
.
2. Обчисліть: 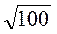 ;
; 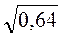 ;
; 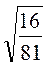 ;
; 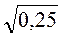 ;
; 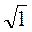 ;
; 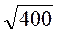 ;
; 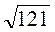 ;
; 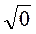 ;
; 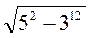 ;
; 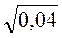 .
.
3. Чи правильна рівність: 32 = (-3); (-7)3 = 73; -27 = (-2)7; |-5| = (-5); |-4|2 = (-4)2; -(-20) = |-20|; |-12| = 12?
4. Яким числом (додатним, від’ємним чи нулем) є значення виразу: (-1)2; -52; (-3)4; (-0,1)5; 153; 07; (-8)11; (-2)0; (-4)12; -(-3)18?
5. Подайте вираз у вигляді квадрата одночлена: a4; y6; 4р8; a2х10; a18k4; 36×12.
V. Відпрацювання вмінь
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв’язати завдання такого змісту:
1. Знаходження значення числового виразу, що має вигляд суми, добутку або відношення виразів виду 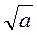 і
і 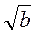 .
.
1) Знайдіть значення виразу: а) 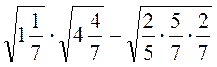 ; б)
; б) 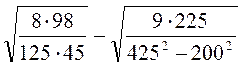 ; в)
; в) 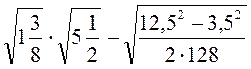 .
.
2) Знайдіть значення виразу: а) 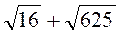 ; б)
; б) 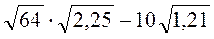 ; в)
; в) 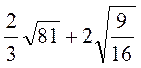 ; г)
; г) 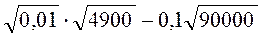 ; д)
; д) 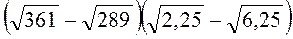 ; є)
; є) 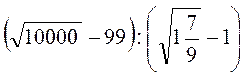 .
.
2. Знаходження значень виразів, що мають вигляд кореня з добутку або частки точних квадратів.
Знайдіть значення виразу:
А) 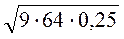 ; б)
; б) 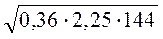 ; в)
; в) 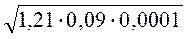 ; г)
; г) 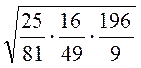 ; д)
; д) 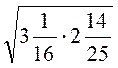 ; є)
; є) 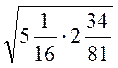 .
.
3. Знаходження значень виразів, що мають вигляд кореня з добутку або частки чисел, які потребують попереднього розкладання на множники.
1) Обчисліть значення кореня: а) 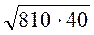 ; б)
; б) 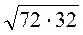 ; в)
; в) 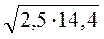 ; г)
; г) 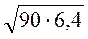 .
.
2) Знайдіть значення виразу: а) 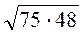 ; б)
; б) 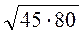 ; в)
; в) 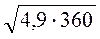 ; г)
; г) 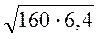 .
.
4. Знаходження значень виразів, що мають вигляд кореня з різниці квадратів.
1) Обчисліть значення виразу: а) 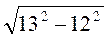 ; б)
; б) 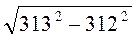 ; в)
; в) 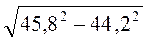 ; г)
; г) 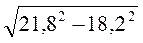 .
.
2) Обчисліть: а) 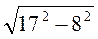 ; б)
; б) 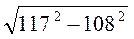 ; в)
; в) 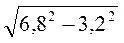 ; г)
; г) 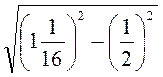 .
.
5. Спрощення виразів, які мають вигляд квадратного кореня з квадрата або парного степеня раціонального виразу (або можуть бути подані в такому вигляді після виконання тотожних перетворень).
1) Спростіть вираз:
А) 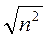 , якщо n < 0; б)
, якщо n < 0; б) 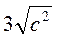 , якщо с > 0; в)
, якщо с > 0; в) 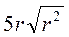 , якщо r > 0; г)
, якщо r > 0; г) 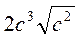 , якщо с > 0; д)
, якщо с > 0; д) 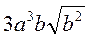 , якщо b < 0; е)
, якщо b < 0; е) 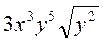 , якщо у > 0.
, якщо у > 0.
2) Знайдіть значення кореня: а) 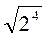 ; б)
; б) 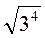 ; в)
; в) 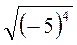 ; г)
; г) 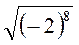 ; д)
; д) 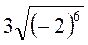 ; є)
; є) 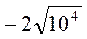 ; ж)
; ж) 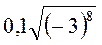 ; з)
; з) 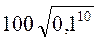 .
.
3) Спростіть вираз: а) 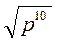 , якщо р > 0; б)
, якщо р > 0; б) 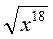 , якщо х < 0; в)
, якщо х < 0; в) 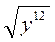 ; г)
; г) 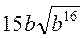 ; д)
; д) 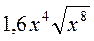 ; є)
; є) 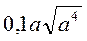 .
.
6. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Знайдіть значення виразу: а)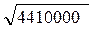 ; б)
; б)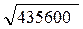 ; в)
; в)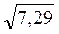 ; г)
; г)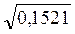 .
.
2) Обчисліть: а) 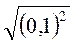 ; б)
; б) 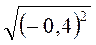 ; в)
; в) 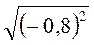 ; г)
; г) 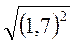 ; д)
; д) 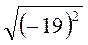 ; є)
; є) 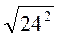 ; ж)
; ж) 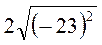 ; з)
; з) 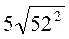 ; и)
; и) 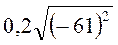 .
.
3) Знайдіть пропущене число:
А)
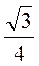
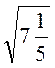
?
Б)
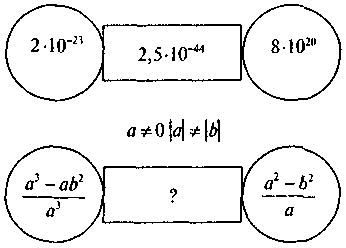
7. На повторення: розв’язати рівняння виду х2 = а.
@ Ha уроці продовжується робота з формування вмінь учнів застосовувати вивчені властивості арифметичного квадратного кореня для обчислення значень числових виразів раціональним способом, а також для перетворення виразів зі змінними, що мають вигляд 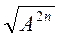 , де А – деякий раціональний вираз.
, де А – деякий раціональний вираз.
VI. Підсумки уроку
Самостійна робота № 8.
Варіант 1 | Варіант 2 |
1. Знайдіть значення виразу: | |
А) Д) | А) Д) |
2. Обчисліть: | |
А) Д) | А) Д) |
3. Спростіть вираз: | |
А) Б) | А) Б) |
VII. Домашнє завдання
1. Вивчити формулювання і способи застосування властивостей арифметичного квадратного кореня, розглянутих на уроках 38-39.
2. Виконати вправи на застосування цих властивостей у прямому та оберненому напрямі.
3. Виконати аналіз самостійної роботи № 8 (за готовими розв’язаннями) та завдання самостійної роботи іншого варіанта.
4. Повторити означення АКК, схему розв’язання рівнянь х2 = а та 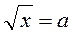 , а також співвідношення між відомими учням числовими множинами та означення чисел, що входять до кожної з вивчених множин (див. тему “Дійсні числа”), а також матеріал, що стосується тотожних перетворень цілих виразів (дії з одночленами та дії з многочленами, зокрема зведення подібних доданків, розкладання многочленів на множники, застосування формул скороченого множення).
, а також співвідношення між відомими учням числовими множинами та означення чисел, що входять до кожної з вивчених множин (див. тему “Дійсні числа”), а також матеріал, що стосується тотожних перетворень цілих виразів (дії з одночленами та дії з многочленами, зокрема зведення подібних доданків, розкладання многочленів на множники, застосування формул скороченого множення).
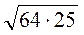 ;б)
;б) 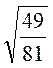 ; в)
; в) 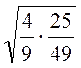 ; г)
; г) 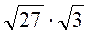 ;
;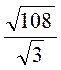 ; є)
; є) 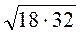 ; ж)
; ж) 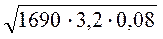
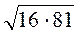 ; б)
; б) 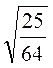 ; в)
; в) 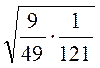 ; г)
; г) 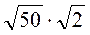 ;
;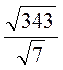 ; є)
; є) 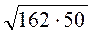 ; ж)
; ж) 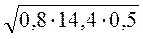
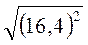 ; б)
; б) 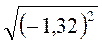 ; в)
; в) 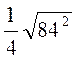 ; г)
; г) 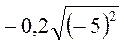 ;
;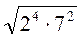 ; є)
; є) 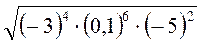 ; ж)
; ж) 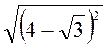
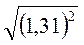 ; б)
; б) 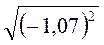 ; в)
; в) 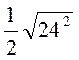 ; г)
; г) 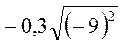 ;
;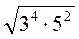 ; є)
; є) 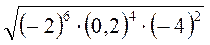 ; ж)
; ж) 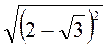
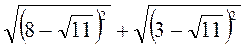 ;
;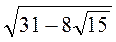
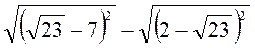 ;
;