Числові і буквені вирази. Формули
УРОК 25
Тема. Числові і буквені вирази. Формули
Мета: сформувати уявлення учнів про формули як ключ до розв’язання цілого класу задач; продовжувати формування вмінь учнів знаходити значення буквених виразів, а також читати їх і складати буквені вирази за умовою задачі.
Тип уроку: засвоєння навичок та вмінь.
Обладнання: таблиця-схема “Формули. Вирази”.
Хід уроку
І. Перевірка домашнього завдання
Математичний диктант
1. Запишіть у вигляді числового виразу, скільки коштує покупка, якщо купили 15 ложок по 2 грн.
2. Запишіть вираз:
А) добуток чисел 3 і 7 [5 і 9];
Б) частка чисел 30 і 5 [50 і 10];
В) сума чисел 60 і добуток чисел 3 і 7 [сума числа 50 і добуток чисел 5 і 9].
3. Запишіть вираз і знайдіть його значення при зазначених числах:
А) різниця х і 15; х = 21 [13 і у; у = 7];
Б) сума 2 і у; у = 19 [х і 3; х = 28];
В) b – b, b – будь-яке [а – 0, а – будь-яке].
II. Актуалізація опорних знань
Частково має місце під час виконання математичного диктанту. Але після виконання і перевірки завдань (можна завчасно проаналізувати
– означення числового виразу; т значення числового виразу;
– буквений вираз;
– як знайти значення буквеного виразу;
– як прочитати вираз, використовуючи назви арифметичних дій.
III. Формування нових знань
Розв’язати задачі за рисунками (рис. 23).

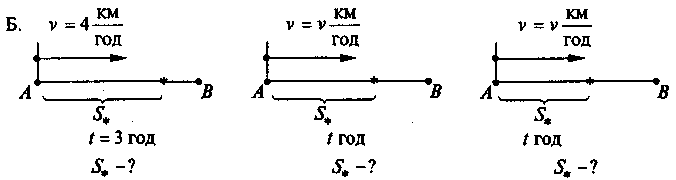
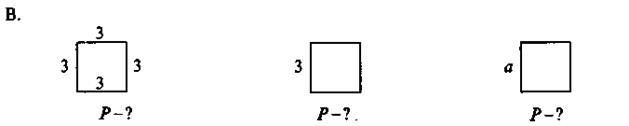
Рис. 23
При цьому на дошці і в зошитах учнів послідовно з’являються записи:
А. Р = 2(3 + 5); | Р = 2(3 + а); | Р = 2(а + b) |
Б. S* = 4 – 3; | S* = v – 3; | S = vt |
В. Р = 3 + 3 + 3 + 3; | Р = 4 – 3. | Р = 4а |
@ Після цього більшість учнів зрозуміли, що задачі кожної групи були схожі і відрізнялись тільки значенням величин, тобто записи, що містяться в останньому стовпчику, є загальним правилом, за яким можна розв’язувати задачі цього виду. Далі вводиться поняття формули (вивішується таблиця-схема).
Таблиця-схема “Формули. Вирази”.
(У зошитах учні роблять запис. Формули S = v – t; P = 2(a + b); Р = 4а.)
Наголошується, що практично для розв’язання всіх задач можна скласти формулу; для цього треба тільки позначити всі величини, що названі в задачі буквами і записати план розв’язання задачі у вигляді рівності, в лівій частині якої – шукана величина, а в правій – буквений вираз.
Далі розглядаються приклади 1-3 з підручника.
Отже, щоб розв’язати задачу, можна скласти рівність, позначивши шукану величину буквою і прирівнявши її до складеного буквеного виразу.
IV. Закріплення знань. Формування вмінь. Розв’язування вправ
№№ 263, 269 – робота з готовими формулами (оформлення розв’язання – дивись приклади 2 і 9, с. 68 підручника).
№№ 271, 273 – складання формул й виконання обчислень за ними.
№ 252, 253 – задачі на повторення вивченого раніше матеріалу.
V. Домашнє завдання
П. 9, № 1-3, № 264; 270; 272; 277.