Числові та лінійні нерівності
УРОК № 60
Тема. Числові та лінійні нерівності
Тестові завдання
1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку?

А) -4 < x < 8;
Б) -4 < х < 8;
В) -4 < х < 8;
Г) -4 < х < 8.
2. Відомо, що х < у. Яка з наведених нерівностей є правильною?
А) 3х < 3у;
Б) x – 3 < y – 3;
В) -3х > -3у;
Г) х + 3 > у + 3.
3. Який із проміжків є розв’язком нерівності 3х + 2 > х – 8?
А) (-?; -5);
Б) (-?; -5];
В) (-5; +?);
Г) [-5; -?).
4. Яка з нерівностей є правильною?
А) 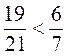
Б) 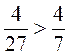 ;
;
В) 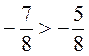 ;
;
Г) 0,(3) > 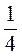 .
.
5. Оцініть довжину сторони квадрата а см, знаючи, що його периметр дорівнює Р см і 0,24 < Р < 0,36.
А) 0,4 < а < 0,6;
Б) 0,6 < а < 0,9;
В) 0,12 < а < 0,18;
Г) 0,24 < а < 0,6.
6. Відомо, що m > 0 і n > 0. Порівняйте з нулем вираз m5n6.
А) m5n6 < 0;
Б) m5n6 > 0;
В) m5n6 ? 0;
Г) m5n6 ? 0.
7. Знайдіть середнє арифметичне всіх цілих чисел з проміжку (-4; 5].
А) 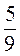 ; б) 1; в) -4,5; г) -1.
; б) 1; в) -4,5; г) -1.
8. Яке з наведених тверджень є неправильним?
А) Якщо почленно додати правильні нерівності одного знака, залишивши їх спільний
Б) Якщо з однієї частини нерівності перенести в іншу доданок з протилежним знаком, то дістанемо нерівність, рівносильну даній.
В) Число m більше від числа n, якщо m – n – додатне число.
Г) Якщо обидві частини нерівності помножити або поділити на будь-яке число, то знак нерівності не зміниться.
Задачі
1. При яких значеннях b різниця дробів 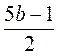 і
і 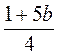 додатна?
додатна?
2. Оцініть значення виразу 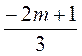 , якщо 2 ? m? 3.
, якщо 2 ? m? 3.
3. При яких значеннях х визначена функція 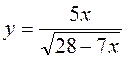 ?
?
4. Розв’яжіть нерівність (х – 1)2 – (х + 2)(х – 3) ? 2х – 1 та запишіть відповідь у вигляді числового проміжку.
5. Доведіть, що вираз (х + 2)(х2 – 2х + 4) – (х2 – 2)(х + 1) набуває додатних значень при всіх дійсних значеннях х. Якого найменшого значення набуває цей вираз і при якому значенні х?
6. Розв’яжіть нерівність 4 – |x + 9| > 3(|x + 9| – 4).
Related posts:
- Лінійні нерівності та їхні системи УРОК № 61 Тема. Лінійні нерівності та їхні системи Тестове завдання 1. Знайдіть переріз проміжків (-6; 7] і (-4; 25]. А) [7; 25); б) [-4; 7); в) (-6; 25]; г) (-4; 7]. 2. Розв’яжіть нерівність . A) k < 1,125; б) k? ; в) k? 1,125; г) немає розв’язків. 3. При яких х має зміст […]...
- Нерівності з однією змінною УРОК № 63 Тема. Нерівності з однією змінною Тестові завдання 1. Дано нерівності: 1) -2х2 + х + 6 < 0; 2) 2х2 + х + 7 ? 0; 3) х2 > 0; 4) -3х2 – х – 6 < 0. 2. Яка з даних нерівностей виконується при будь-яких значеннях x? а) усі; б) 2; […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Лінійні нерівності з однією змінною УРОК № 12 Тема. Лінійні нерівності з однією змінною Мета уроку: домогтися закріплення учнями змісту: означення рівносильних нерівностей та властивостей рівносильних нерівностей; означення лінійної нерівності з однією змінною та схеми Ті розв’язування залежно від різних значень коефіцієнтів. Доповнити знання учнів уявленням про схему дій при розв’язування нерівностей з однією змінною, що містять дроби із числовими […]...
- Числові нерівності. Доведення числових нерівностей УРОК № 2 Тема. Числові нерівності. Доведення числових нерівностей Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст […]...
- ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ РОЗДІЛ 1 ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА § 4. ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ Ви вже знаєте чотири арифметичні дії над числами – додавання, віднімання, множення і ділення. Щоб записати, яку саме дію над числами треба виконати, використовують числові вирази. Наприклад, записи 24 + 2, 24 – 2, 24 ∙ 2, 24 : 2 […]...
- Логарифмічні нерівності Математика – Алгебра Логарифмічна функція Логарифмічні нерівності Розв’язуючи логарифмічні нерівності, спираються на такі твердження. 1. Якщо , то нерівність рівносильна подвійній нерівності . Це твердження можна записати у вигляді: або 2. Якщо , то нерівність рівносильна подвійній нерівності . Це твердження можна записати у вигляді: або Зверніть увагу: при розв’язуванні логарифмічної нерівності немає сенсу окремо […]...
- Числові та буквені вирази Математика – Алгебра Натуральні числа і дії над ними Числові та буквені вирази Числовий вираз складається з чисел, знаків дій та дужок. Якщо виконати всі зазначені дії у правильному порядку, дістанемо число, яке називається значенням числового виразу. Порядок виконання дій: 1. Обчислюють квадрати та куби чисел, які зустрічаються у виразі. 2. Виконують дії в дужках. […]...
- Рівняння. Нерівності зі змінною Рівняння. Нерівності зі змінною 1 Розбий записи на дві групи. Назви кожну групу. 27 + х = 51 27 + х < 51 40 ∙ р > 160 2 Згадай, що ти знаєш про рівняння; про нерівності зі змінною. Розглянь, як учні розв’язали рівняння та нерівність способом добору. Прокоментуй їхні дії. Із чисел 1, 2, […]...
- Рівняння. Нерівності зі змінною Мета: узагальнити й систематизувати навчальний досвід учнів відносно рівнянь і нерівностей зі змінною, способів їх розв’язування. Дидактичні задачі. Вдосконалювати навички позатабличного множення та ділення – усна лічба. Класифікувати записи на рівності та нерівності зі змінною. Актуалізувати поняття рівняння, “розв’язок рівняння”, “розв’язати рівняння”; поняття нерівності зі змінною; розуміння способу добору числа для розв’язування рівнянь та нерівностей. […]...
- Розв’язування нерівностей з однією змінною Математика – Алгебра Нерівності Розв’язування нерівностей з однією змінною Розв’язком нерівності з однією змінною називається значення цієї змінної, яке перетворює її на правильну числову нерівність. Розв’язати нерівність означає знайти всі її розв’язки або довести, що їх немає. Дві нерівності називають Рівносильними, якщо вони мають одні й ті самі розв’язки або не мають розв’язків. Числові проміжки […]...
- Рівняння. Нерівності. Геометричний матеріал Рівняння. Нерівності. Геометричний матеріал 753. Прочитайте твердження. До кожного з них доберіть відповідне рівняння. 1. Невідоме число збільшили у 6 разів і отримали число 4206. 2. Різницю чисел х і 215 збільшили у 6 разів і отримали число 2916. 3. Невідоме число зменшили на добуток чисел 215 і 6 та отримали число 3246. 4. Невідоме […]...
- Числові і буквені вирази. Формули. Властивості додавання і віднімання УРОК 26 Тема. Числові і буквені вирази. Формули. Властивості додавання і віднімання Мета: закріпити знання учнів про основні поняття теми (числові і буквені вирази, формули, значення числового виразу); продовжувати відпрацьовувати навички складання і знаходження значень буквених виразів при зазначених значеннях змінних, повторити тему “Додавання і віднімання”; підготовити учнів до тематичної контрольної роботи № 2. Тип […]...
- Повторення. Математичні вирази, рівності та нерівності Повторення. Математичні вирази, рівності та нерівності 1 Розбий математичні вирази на дві групи. Прочитай математичні вирази різними способами. 420 + 350 618 – а х + у 920 – 460 7 ∙ с 151 ∙ 4 408 : 3 n : 14 Значення яких виразів ти можеш знайти? Знайди їх значення. Чого не вистачає, щоб […]...
- Лінійні рівняння з однією змінною 793. Лінійними рівняннями є рівняння: а) 2/9х = 8; в) -2,7y = 0. 794. а) 56х = 64; рівняння має 1 корінь, Б) 0х = -2; рівняння не має коренів; В) 8х = 0; рівняння має 1 корінь, х = 0; Г) 0у = 0; рівняння має безліч коренів. 795. а) 6х = 42; х […]...
- Числові функції. Зростаючі і спадні, парні і непарні функції УРОК 1 Тема. Числові функції. Зростаючі і спадні, парні і непарні функції Мета уроку: Узагальнення і систематизація знань учнів про числові функції (область визначення і область значення функцій, зростаючі і спадні функції, парні і непарні функції). І. Мотивація навчання Процеси реального світу тісно пов’язані між. собою. Серед різноманіття явищ вчені виділили такі, у яких взаємозв’язок […]...
- Розв’язування найпростіших тригонометричних нерівностей УРОК 29 Тема. Розв’язування найпростіших тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: tg t > a, tgt < a, ctg t < a, ctg t > a (tgt a, tgt a, ctg t a, ctg t a). І. Перевірка домашнього завдання 1. Відповіді на запитання, які виникли в учнів у процесі […]...
- Числові проміжки. Переріз і об’єднання проміжків УРОК № 10 Тема. Числові проміжки. Переріз і об’єднання проміжків Мета уроку: домогтися засвоєння учнями змісту понять: числовий проміжок, переріз та об’єднання числових проміжків, а також усвідомлення учнями існування різних видів числових проміжків, що відповідають різним видам нерівностей. Розпочати роботу з вироблення вмінь відтворювати зміст вивчених понять, записувати числові проміжки, що відповідають різним видам нерівностей […]...
- Властивості числових нерівностей Математика – Алгебра Нерівності Властивості числових нерівностей a, b, с, d – довільні числа. 1. Якщо і , то . 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність. 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. […]...
- Числові функції Математика – Алгебра Числові функції Залежність змінної y від змінної x називається Функцією, якщо кожному значенню x відповідає єдине значення y. x називається Аргументом, або Незалежною змінною, y – Залежною змінною, або Функцією від x. Позначення: , і т. д. Множина значень, яких набуває незалежна змінна x, називається областю визначення функції. Позначення: , і т. […]...
- Аналіз підсумкової контрольної роботи. Розв’язування цікавих задач УРОКИ № 68, 69 Тема. Аналіз підсумкової контрольної роботи. Розв’язування цікавих задач Задачі підвищеної складності 1. При яких значеннях а рівняння не має дійсних коренів? 1) х2 + 4х – а = 0; 2) (а – 1)х2 + (2а – 3)х + а = 0; 3) (а – 2)х2 – 2(а – 3)х + а […]...
- РОЗВ’ЯЗУВАННЯ ТА СКЛАДАННЯ ЗАДАЧ НА ПРОПОРЦІЙНЕ ДІЛЕННЯ. РІВНЯННЯ І НЕРІВНОСТІ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ЗАКРІПЛЮВАТИ ВМІННЯ СКЛАДАТИ ЗАДАЧІ НА ПРОПОРЦІЙНЕ ДІЛЕННЯ; ДОСЛІДИТИ МОЖЛИВОСТІ ПЕРЕБУДОВИ ЗАДАЧ НА ЗАДАЧІ НА ПРОПОРЦІЙНИЙ ПОДІЛ I. Перевірка домашнього завдання Фронтально скласти план розв’язування задачі 847. Взаємоперевірка обчислення виразів вправи 848. II. Актуалізація та корекція опорних знань учнів 1. Усні обчислення. Змагання двох команд гравців. 1 команда 2 команда 350 • (430 […]...
- Розв’язування тригонометричних нерівностей УРОК 30 Тема. Розв’язування тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати тригонометричні нерівності. І. Перевірка домашнього завдання. 1. Відповіді на запитання, які виникли у учнів при виконанні домашнього завдання. 2. Фронтальна бесіда з учнями з використанням рис. 135. 1) Які дуги відповідають нерівностям: Tg t > a, tg t < a, tg t > […]...
- Числові і буквені вирази. Формули УРОК 25 Тема. Числові і буквені вирази. Формули Мета: сформувати уявлення учнів про формули як ключ до розв’язання цілого класу задач; продовжувати формування вмінь учнів знаходити значення буквених виразів, а також читати їх і складати буквені вирази за умовою задачі. Тип уроку: засвоєння навичок та вмінь. Обладнання: таблиця-схема “Формули. Вирази”. Хід уроку І. Перевірка домашнього […]...
- Числові вирази. Буквені вирази та їх значення. Формули Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 10. Числові вирази. Буквені вирази та їх значення. Формули Приклад 1. Поїзд проїхав за першу годину 60 км, а за другу – на 5 км більше. Скільки кілометрів проїхав потяг за дві години? Розв’язання. За другу годину потяг проїхав 60 + 5 […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Числові й буквені вирази Урок № 41. Тема. Числові й буквені вирази Мета уроку. Закріпити в учнів навики розв’язування вправ на спрощення та обчислення буквених виразів в знайомих і змінених ситуаціях. Розвивати здібності на основі розумових дій т а операцій. Виховувати вміння творчо працювати. Обладнання. Таблиця “Порядок дій”, дидактичні матеріали. Хід уроку І. Повідомити тему, мету уроку. ІІ. Перевірка […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- ЧИСЛОВІ ВИРАЗИ РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ У розділі дізнаєтесь: · про числові вирази та їх види; · чим відрізняються числовий вираз і вираз зі змінними; · що таке допустимі значення змінних у виразі; · які вирази називають цілими; · як обчислювати значення виразу зі змінними; · про способи спрощення виразів; · яка рівність е тотожністю та […]...
- Вирази. Числові вирази Урок № 12 Тема. Вирази. Числові вирази Мета: систематизувати та узагальнити знання про числові й буквені вирази, набуті учнями в 5-6 класах. Тип уроку: систематизація та узагальнення знань. Хід уроку І. Аналіз тематичної контрольної роботи Про результати попереднього уроку (тематична контрольна робота № 1) учні дізнаються до уроку (учитель може роздати зошити із тематичної контрольної […]...