ЧИСЛОВІ ВИРАЗИ
РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ
У розділі дізнаєтесь:
· про числові вирази та їх види;
· чим відрізняються числовий вираз і вираз зі змінними;
· що таке допустимі значення змінних у виразі;
· які вирази називають цілими;
· як обчислювати значення виразу зі змінними;
· про способи спрощення виразів;
· яка рівність е тотожністю та як її доводити;
· як застосувати вивчений матеріал на практиці

&1. ЧИСЛОВІ ВИРАЗИ
Із курсу математики 5-6 класів ви знаєте,
Запис, у якому використовують тільки числа, знаки арифметичних дій і дужки, називається числовим виразом.
Наприклад, записи 15 + 3,15 – 3, 15 ∙ 3,15 : 3 є числовими
Виразами. їх називають відповідно сумою, різницею, добутком і часткою чисел 15 і 3. У кожному із цих виразів числа 15 і 3 є компонентами виразу. Вираз 153 також є числовим. Його називають степенем числа 15. У ньому число 15 – основа степеня, а число 3 – показник степеня.
Якщо виконати арифметичну дію у виразі, то дістанемо число – значення числового
Зверніть увагу:
Числовий вираз показує, яку арифметичну дію (дії) треба виконати над числами, але не показує результат цієї дії (дій).
Ви знаєте, що дії додавання і віднімання є діями першого ступеня, дії множення і ділення – другого ступеня, а піднесення до степеня – третього ступеня. Обчислюючи значення числового виразу, спочатку з’ясовують, дії яких ступенів містить вираз, а потім виконують дії, дотримуючись відомого вам порядку виконання дій.
Задача 1. Знайдіть значення числового виразу:
1)35 – 15 + 9; 2) 35 : 7 + 4 . 23.
Розв’язання. 1. Даний вираз містить тільки дії першого ступеня, тому ці дії виконують за порядком написання зліва направо:
2. Вираз 35 : 7 + 4 ∙ 23 містить дії трьох ступенів, тому спочатку виконують дію третього ступеня, потім – дії другого ступеня (зліва направо), а після цього – дію першого ступеня:
35 : 7 + 4 ∙ 23 = 35 : 7 + 4 ∙ 8 = 5 + 4 ∙ 8 = 5 + 32 = 37.
Чи залежить значення числового виразу від того, які у ньому розставлено дужки? Так. Наприклад, вирази 4 + (30 : 6 – 1) і 4 + 30 : (6 – 1) мають різні значення: 4 + (30 : 6 – 1) = 8, а 4 + 30 : (6 – 1) = 10. Отже, можемо записати:
4 + (30 : 6 – 1) ≠ 4 + 30 : (6 – 1).
Зверніть увагу:
Дужки у виразі змінюють порядок виконання дій.
Задача 2. Чи можна знайти значення числового виразу
25 : (3 ∙ 8 – 23 – 1)?
Розв’язання. Даний вираз містить ділення числа 25 на вираз, що стоїть у дужках. Виконавши дії в дужках, дістанемо: 3 ∙ 8 – 23 – 1 = 24 – 23 – 1 = 0. Отже, щоб знайти значення заданого виразу, треба число 25 поділити на 0. А це зробити неможливо. Тому значення даного числового виразу знайти не можна.
Коротко говорять: “Даний вираз не має значення” або “Даний вираз не має змісту”.
Зверніть увагу:
– ділити на 0 не можна;
– вираз, що містить ділення на нуль, не має змісту.
Узагальнимо відомості про порядок виконання дій у виразах.
Порядок виконання дій у виразах.
1. У виразі, що містить дії тільки одного ступеня, дії виконують у тому порядку, у якому вони записані.
2. У виразі, що містить дії трьох ступенів, першими виконують дії старшого ступеня в тому порядку, у якому вони записані.
3. У виразі з дужками спочатку виконують дії в дужках, а потім – інші дії за відомим порядком.
Дізнайтеся більше

1. У курсі математики 5 – 6 класів і в цьому параграфі ви зустрічали речення, які містять слова “називають” або “називається”. Це означення понять. В означенні розкривається зміст поняття. Наприклад, в означенні числового виразу вказується властивість, за допомогою якої можна відрізнити числовий вираз від будь-яких інших записів. Раніше вам зустрічалися записи 3 * 5 + 4, 2 ∙ 3 = 6, (а + 100) ∙ 2. Їх не можна вважати числовими виразами, оскільки вони не задовольняють означення числового виразу. Справді, перший запис містить знак *, що не є знаком арифметичної дії. Другий запис містить знак рівності, а третій – букву.
2. Граве Дмитро Олександрович (1863-1939) – видатний математик, фундатор вітчизняної алгебраїчної школи, академік Академії наук УРСР (1919), почесний член АН СРСР (1929). Закінчив Санкт-Петербурзький університет (1885). У 1896 р. захистив дисертацію на ступінь доктора математики “Про основні завдання математичної теорії побудови географічних карт”. Працював професором Харківського (1897), а потім Київського (1899) університетів. У1934 став першим директором Інституту математики АН УРСР. Створив у Києві наукову алгебраїчну школу. Основні праці стосуються алгебри, прикладної математики, механіки, кібернетики, астрономії. Його “Трактат з алгебраїчного аналізу”, який побачив світу 1938, мав значний вплив на розвиток математики 20 ст.
Його учнями були Б. Делоне, М. Кравчук, М. Чеботарьов, О. Шмідтта ін.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що називається числовим виразом? Наведіть приклади.
2. Що називають значенням числового виразу?
3. Який порядок виконання дій у числовому виразі без дужок?
4. У якому порядку треба виконувати дії в числовому виразі з дужками?
5. У якому випадку числовий вираз не має змісту?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
1. Чи є числовим виразом запис:
1)14 : 2 + 5; 3)24 – 14 = 10; 5)4 ∙ х = 20;
2) 27 > 4 ∙ 3; 4) 5  – 2 ∙ 5,2; 6) 84 + 42?
– 2 ∙ 5,2; 6) 84 + 42?
Відповідь поясніть.
2. Наведіть приклад виразу, який для двох чисел є:
1) сумою; 2) різницею; 3) добутком; 4) часткою; 5) степенем.
3. Чи правильно, що значенням числового виразу є: 1) буква; 2) слово; 3) речення; 4) сам числовий вираз; 5) число, яке отримали, виконавши дію в заданому виразі на одну дію; 6) число, яке отримали, правильно виконавши дію в заданому виразі на одну дію; 7) число, яке отримали, правильно виконавши якусь одну дію в заданому виразі на кілька дій; 8) число, яке отримали, правильно виконавши всі дії в заданому виразі на кілька дій?
4. У якому порядку треба виконувати дії в числовому виразі, що містить дії: 1) першого ступеня; 2) другого ступеня; 3) першого і другого ступенів; 4) третього ступеня; 5) другого і третього ступенів; 6) усіх трьох ступенів?
5. Чи правильно, що дужки у виразі: 1) не змінюють порядок виконання дій; 2) змінюють порядок виконання дій?
6. Наведіть приклади числових виразів, які: 1) мають зміст; 2) не мають змісту.
7. Чи правильно, що не має змісту вираз:
1)5 – 0; 3)5 ∙ 0; 5)5 – (3 – 3); 7)5 ∙ (3 – 3);
2)5 + 0; 4)5 : 0; 6)5 + (3 – 3); 8)5 : (3 – 3)?
8. Значенням якого виразу є число 2:
1)24 : 6 – 3;
2)(20 – 4) : 8;
3) 32 – 23;
4)10 – 4 ∙ 2?
9. Значенням якого виразу є число 5:
1) 25 – 15 : 3;
2) (42 + 9) : 5?
10. Назвіть порядок виконання дій для обчислення значення числового виразу 5 + 2 ∙ 4 – 18 : 32. Знайдіть значення виразу.
11. Дано числа 2,5 і 4. Складіть числовий вираз, який є їх:
1) сумою; 2) різницею; 3) добутком; 4) часткою. Скільки числових виразів можна отримати? Знайдіть значення цих виразів.
12. Дано числа 2 і 3. Складіть вирази для піднесення одного числа до степеня іншого. Скільки числових виразів можна отримати? Знайдіть значення цих виразів.
13. Дано числа 5 і 2. Складіть числовий вираз, який є: 1) сумою чисел; 2) різницею чисел; 3) добутком чисел; 4) часткою чисел; 5) степенем, у якому одне число підноситься до степеня іншого. Знайдіть значення цих виразів.
14. Знайдіть значення виразу:
1) 15,6 + 27,8;
2) 14,275 + 10,8;
3) 45,5 – 23,4;
4) 84,6 – 12,49;
5) 12,3 ∙ 5,8;
6) 0,28 ∙ 0,125;
7) 48,56 : 1,6;
8) 0,15 : 1,25;
9) 1,8 : 0,24.
Якими правилами виконання дій з десятковими дробами ви скористалися?
15. Знайдіть значення виразу:
1) 42,5 + 12,52;
2) 34,6 – 15,54;
3) 2,8 ∙ 0,15;
4) 56,28 : 1,4.
16. Виконайте дії:
1) 12  + 8
+ 8  ;
;
2) 16  + 2
+ 2  ;
;
3) 7 – 2 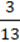 ;
;
4) 8 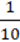 – 5
– 5  ;
;
5) 2  ∙
∙ 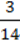 ;
;
6) 5  ∙ 3
∙ 3  ;
;
7) 2  : 1
: 1 ;
;
8) 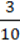 : 2
: 2 .
.
+
Якими правилами виконання дій зі звичайними дробами ви скористалися?
17. Виконайте дії:
1) 16  + 14
+ 14 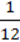 ;
;
2) 21 – 9
– 9 ;
;
3) 9  ∙ 7;
∙ 7;
4) 5 : 7
: 7  .
.
18. Обчисліть:
1) 22;
2) 53;
3) 35;
4) 71;
5) 43;
6) 17;
7) (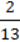 );
);
8) (5  )2
)2
Сформулюйте правило піднесення числа а до степеня n, яким ви скористалися.
19. Обчисліть:
1) 24;
2) 33;
3) 45;
4) (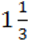 )2.
)2.
20. Обчисліть:
1) -45,2 + 12,15;
2) 25 – 38  ;
;
3) -4  – 1,25;
– 1,25;
4) -2,5 ∙ 1,2;
5) -2,8 ∙ (- );
);
6) – 14  : (-43).
: (-43).
Сформулюйте правила виконання дій з раціональними числами, якими ви скористалися.
21. Обчисліть:
1)-14,7 + 10,15;
2)-12  – 3,5;
– 3,5;
3)4,08 ∙ (- );
);
4) -12,6:(-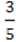 ).
).
22. Чи змінять дужки порядок виконання дій у виразі 20 + 5 ∙ 23 – 6 : 2, якщо їх розставити так:
1) (20 + 5) ∙ 23 – 6 : 2;
2) 20 + (5 ∙ 23 – 6) : 2;
3) (20 + 5 ∙ 23) – 6 : 2;
4) 20 + 5 ∙ (23 – 6 : 2)?
Відповідь поясніть.
23. У якому порядку треба виконувати дії в числовому виразі з дужками, що містить дії: 1) першого і другого ступенів; 2) другого і третього ступенів; 3) усіх трьох ступенів? Скільки випадків потрібно розглянути? Наведіть приклади.
24. Запишіть у вигляді виразу і знайдіть його значення:
1) добуток суми чисел 3,5 і -4,5 та числа 42;
2) різниця числа 4,67 та добутку чисел 2,18 і 0,5;
3) сума квадрата числа 3 і числа 5  ;
;
4) різниця куба числа 4 і числа -0,1;
5) добуток числа 3 і квадрата числа – 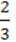 ;
;
6) частка суми чисел 3,2 і  та числа 0,5.
та числа 0,5.
25. Запишіть у вигляді виразу і знайдіть його значення:
1) добуток числа -2,5 та суми чисел 34,8 і -2,8;
2) різниця квадрата числа 1,2 і куба числа 4;
3) сума числа 5  та частки чисел 5 і 7;
та частки чисел 5 і 7;
4) частка числа 2,5 та добутку чисел 1 і
і 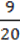 .
.
26. Перевірте, чи має зміст вираз:
1) 2,5 – (1,4 – 7 ∙ 0,2);
2) 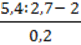 ;
;
3) 5 ∙ 2,04 + 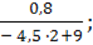
4) 2  : (17,5 – 8
: (17,5 – 8  ∙ 2)
∙ 2)
Чи потрібно виконувати всі дії? Відповідь поясніть.
27. Чи має зміст вираз:
1) 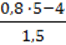 ;
;
2) 12 + 28 : (15 ∙ 0,2 – 3)?
28. Складіть числовий вираз, значення якого дорівнює:
1) 14;
2) – 5;
3) 2 ;
;
4) – 0,5.
29. Складіть числовий вираз, значення якого дорівнює:
1) 20;
2) -5 .
.
30. Знайдіть значення виразу:
1) 0,12 ∙ 10 + 2,4 ∙ 5 ∙ 12 ∙ 9 : 1,8;
2) (15 ∙ 0,012 + 15 : 102) : 0,66 – 1,82;
4) (3,4 + 5,1) ∙ 1 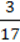 + (1
+ (1 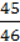 – 2
– 2 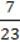 ) :
) : 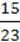 .
.
31. Знайдіть значення виразу:
1) 2,5 ∙ 23 + 7,5 ∙ (0,04 + 1,62) – 1,8 : 90;
2) (4 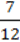 – 3
– 3 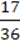 ) : 1
) : 1 + 4
+ 4  ∙ (-
∙ (- 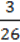 ) + 2,5.
) + 2,5.
32. Виконайте дії:
1) 6 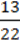 – 5
– 5 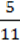 : 4 +
: 4 +  ∙
∙ 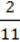 +
+  :
: 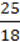 ;
;
2) 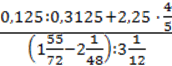 – 3,6;
– 3,6;
3) 1,2 : (0,171: 0,9 – 0,028 ∙ 2,5) + 0,8 ∙ (3 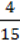 + 1
+ 1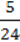 – 3
– 3 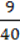 ) – 0,075 : 3 : 400;
) – 0,075 : 3 : 400;
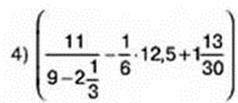 : 0,016 – 0,005 ∙ 10 500.
: 0,016 – 0,005 ∙ 10 500.
33. Виконайте дії:
1) (10 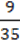 – 8
– 8 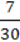 ) : + 4 ∙ (1,35 : 0,9 – 1,5 ∙
) : + 4 ∙ (1,35 : 0,9 – 1,5 ∙  ) + 0, 204 ∙ 25 – 7,1;
) + 0, 204 ∙ 25 – 7,1;
2) 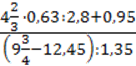 – 12,5 : 1
– 12,5 : 1 .
.
34. У 7-А класі навчаються 25 учнів, у 7-Б класі – на 2 учні більше, ніж у 7-А класі, а в 7-В класі – на 5 учнів менше, ніж у 7-Б класі. Скільки учнів навчаються в цих класах разом? Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
35. На першій полиці стоять 18 книг, на другій – на 4 книги менше, ніж на першій, а на третій – стільки книг, як на першій і другій полицях разом. Скільки книг стоять на трьох полицях разом? Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
36. Яке число треба поставити замість зірочки, щоб вираз не мав змісту:
1) 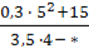
2) 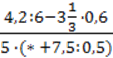 ?
?
37. Яке число треба поставити замість зірочки, щоб вираз не мав змісту:
1) 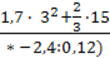 ?
?
38. У виразі 1,5 –  : 3
: 3  +
+  ∙ 4,52 розставте дужки так, щоб значення виразу було: 1) найбільшим; 2) найменшим.
∙ 4,52 розставте дужки так, щоб значення виразу було: 1) найбільшим; 2) найменшим.
39. Обчисліть зручним способом:
1) 9 + 99 + 999 + 9999 + 99 999;
2) 1 -2 + 3 – 4 +…+999 – 1000:
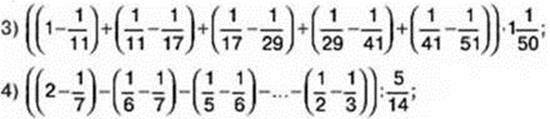
5) 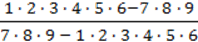 ;
;
6) 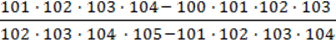
40. Розв’яжіть рівняння:
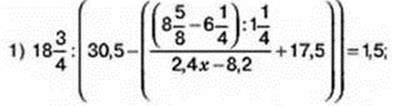
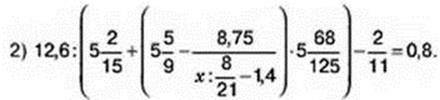
41. Розставте числа від 1 до 9 в кружечках на малюнку 1 так, щоб сума чисел на кожній стороні трикутника дорівнювала 20.
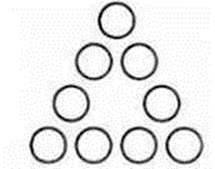
Мал. 1
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
42. Скільки пляшок ємністю 250 мл знадобиться бабусі, щоб розлити в них 5 л соку? Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
43. У бензобак машини вміщується 45 л бензину. Витрати бензину становлять 8,5 л на кожні 100 км шляху. Машина вирушила в подорож з повним бензобаком і проїхала 300 км. Обчисліть, скільки літрів бензину залишилось у бензобаку після закінчення подорожі. Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
44. Складіть задачу про свій вік і вік інших членів своєї родини. Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
45. Складіть задачу про кількість хлопців і дівчат у вашому класі. Складіть числовий вираз для розв’язування задачі та знайдіть його значення.
ЗАДАЧІ НА ПОВТОРЕННЯ
46. Знайдіть:
1) 0,5 числа 300;
2) 0,15 числа 90;
3)  числа 21;
числа 21;
4) 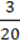 – числа 0,8. 20
– числа 0,8. 20
47. Знайдіть число, якщо:
1) його 0,3 дорівнюють 24;
2) його 0,25 дорівнюють 0,25;
3) його 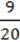 дорівнюють 270;
дорівнюють 270;
4) його 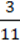 дорівнюють 0,3.
дорівнюють 0,3.
48. трьох шостих класах школи навчаються 84 учні. Кількість учнів 7-Б класу становить 75 % кількості учнів 7-А класу, а кількість учнів 7-В класу – 50 % кількості учнів 7-А і 7-Б класів разом. Скільки учнів навчаються в кожному класі?