Головна ⇒ 📌Довідник з геометрії ⇒ Циліндр, описаний навколо кулі
Циліндр, описаний навколо кулі
Геометрія
Комбінації геометричних тіл
Циліндр, описаний навколо кулі
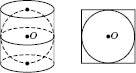
Площина, проведена через центр кулі паралельно твірним циліндра (рисунок нижче зліва), є площиною симетрії тіла. У цьому випадку висота циліндра дорівнює діаметру кулі. В осьовому перерізі цього тіла отримаємо прямокутник, у який вписане коло (рисунок справа). Але із цього випливає, що осьовий переріз даного циліндра – квадрат. Отже, діаметр циліндра дорівнює діаметру кулі.
Related posts:
- Циліндр, вписаний у кулю Геометрія Комбінації геометричних тіл Циліндр, вписаний у кулю Основи циліндра є рівновіддаленими від центра кулі (рисунок нижче зліва). Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра. У перерізі тіла такою площиною дістанемо прямокутник і описане навколо нього коло (рисунок справа). Прямокутник ABCD є осьовим перерізом циліндра, а […]...
- Вписані кулі Геометрія Комбінації геометричних тіл Вписані кулі Якщо куля вписана в призму, то в її перпендикулярний переріз можна вписати коло. Висота призми дорівнює діаметру кола, вписаного в перпендикулярний переріз призми, тобто діаметру вписаної кулі. Центр кулі – середина висоти призми, що проходить через центр кола, яке вписане в перпендикулярний переріз. Центр кулі, яка вписана в пряму […]...
- Куля, вписана в конус Геометрія Комбінації геометричних тіл Куля, вписана в конус Площина, яка містить вісь конуса, є площиною симетрії (рисунок нижче зліва). Осьовий переріз комбінації є рівнобедреним трикутником, у який вписане коло (рисунок справа). Трикутник – це осьовий переріз конуса, тобто – твірні конуса, AB – діаметр основи конуса, а коло – велике коло вписаної кулі. Отже, радіус […]...
- Циліндр Геометрія Тіла обертання Циліндр Круговим циліндром називається тіло, яке складається з двох кругів, що не лежать в одній площині й суміщаються паралельними перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (див. рисунок). Круги називаються Основами циліндра, а відрізки, що сполучають точки кіл кругів, – Твірними циліндра. Основи циліндра рівні й лежать у паралельних […]...
- Конус, вписаний у кулю Геометрія Комбінації геометричних тіл Конус, вписаний у кулю Вершина конуса лежить на сфері (рисунок нижче зліва). Основа конуса лежить на сфері. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі дістанемо трикутник, вписаний у коло (рисунок справа). Трикутник рівнобедрений. Бічні сторони – твірні конуса, коло – велике коло описаної кулі. Отже, радіус […]...
- Об’єм кулі Геометрія Об’єми тіл Об’єм кулі На рисунку зображено кулю, кульовий сегмент і кульовий сектор. Об’єм кулі: , де R – радіус кулі. Об’єм кульового сегмента: , де H – висота кульового сегмента, R – радіус кулі. Об’єм кульового сектора: , де R – радіус кулі, H – висота відповідного кульового сегмента. Іноді треба знайти об’єм […]...
- Циліндр. Площа поверхні та об’єм циліндра УРОК № 56 Тема. Циліндр. Площа поверхні та об’єм циліндра Мета уроку: повторення, приведення в систему й розширення відомостей про циліндр, площу поверхні та об’єм циліндра; формування вмінь учнів знаходити площі поверхонь і об’єми циліндрів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі циліндрів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
- ЦИЛІНДР. КОНУС. КУЛЯ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ § 18. ЦИЛІНДР. КОНУС. КУЛЯ У 5 класі ви вже ознайомилися з просторовими фігурами: прямокутним паралелепіпедом і кубом. ь на малюнок 56. Ви бачите предмети, які використовують у побуті. У сі вони мають одну й ту саму форму – циліндра (мал. 57). Мал. 56 Мал. 57 Мал. 58 Maл. 59 […]...
- Описані кулі Геометрія Комбінації геометричних тіл Описані кулі Кожна грань вписаного у сферу многогранника є вписаним у деяке коло многокутником. Основи перпендикулярів, які опущені з центра описаної кулі на площини граней, є центрами описаних навколо граней кіл. Отже, центром кулі, описаної навколо многогранника, є точка перетину перпендикулярів до площини граней, які проведені через центри кіл, описаних навколо […]...
- Тіла обертання 1008. Осьовий переріз – це ΔARB1, де BB1 = 2 × СВ = 4 (см), АС + В 1В, В 1C = СB. S = 4 см2. 1009. Sб. ц. = 2πrh = 2π × 2 × 10 = 40π (см2), Sб = 40π см2. 1010. Sб. ц. = 4 × 5 = 20 (см2), […]...
- Об’єм кулі та її частин 1338. А) Нехай ABCDA1В1C1D1 – куб. Оскільки куля вписана в куб з ребром а, то 2г = а, Отже, об’єм кулі Б) Оскільки діагональ куба дорівнює двом радіусам кулі, то знайдемо діагональ З ΔB1BD: Отже, радіус, кулі Об’єм кулі V дорівнює: Відповідь: а) б) 1339. Нехай SA – твірна конуса. ∠SAO = α. З ΔSAO: […]...
- Об’єми кулі та її частини. Площа сфери 1. Обчислимо площу поверхні Землі: S= 4πR2 = 4π · 63752. Площа суші складає Відповідь: π × 63752. 2. Знайдемо об’єм кавуна радіуса 10 см: На одного їдока приходиться Знайдемо об’єм кавуна-радіусом 20 см: На одного їдока приходиться Відповідь: у вісьмох. 3. Оскільки передбачається, що каша у двох котлах однакова, То в другому казані відношення […]...
- Циліндр 940. Нехай дано циліндр, ABCD – осьовий переріз циліндра, AO = r – радіус циліндра, AC = d – діагональ осьового перерізу: А) ΔABC — прямокутний. BC – висота циліндра; Б) SABCD – площа діагонального перерізу. В) Площа бічної поверхні: Г) Площа поверхні циліндра 941. Нехай дано циліндр, діагональ осьового перерізу циліндра дорівнює D і […]...
- Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...
- Вписаний та описаний чотирикутники – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Вписаний та описаний чотирикутники Якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло: A + C = 180°, B + D = 180°. Якщо суми протилежних сторін чотирикутника рівні, то в нього можна вписати коло: AB + CD = BC + AD...
- Властивості сфери і кулі 1. Відстань, яка б відділяла мене від мого антипода дорівнювала б Двом радіусам Землі. Відповідь: 2R Землі. 2. Нехай АО – радіус Землі, ОА = 6400 км, О1А – радіус Полярного кола Землі. Координати Полярного кола Землі 66°31′ п. ш. ∠АОВ = 66°31′; ∠О1ОА = 90° – 67° = 23°. З ΔO1ОA: Ο1Α = ОА […]...
- Куля. Площа поверхні та об’єм кулі УРОК № 58 Тема. Куля. Площа поверхні та об’єм кулі Мета уроку: повторення, приведення в систему й розширення відомостей про кулю (сферу), площу поверхні та об’єм кулі; формування вмінь учнів знаходити площі поверхонь і об’єми куль. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі куль. Вимоги до рівня підготовки учнів: пояснюють, […]...
- Об’єми круглих тіл Геометрія Об’єми тіл Об’єми круглих тіл Об’єм циліндра (див. рисунок) дорівнює добутку площі його основи та висоти. ; . Об’єм конуса (див. рисунок) дорівнює одній третині добутку площі його основи та висоти. . . Об’єм зрізаного конуса (див. рисунок): ....
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Об’єми многогранників Геометрія Об’єми тіл Об’єми многогранників Об’єм будь-якої призми дорівнює добутку площі основи та висоти. . На рисунках наведені приклади призм із різними основами. Для прямокутного паралелепіпеда отримаємо , де a, b, c – його виміри. Для куба , де a – довжина ребра. Для похилої призми (рисунок нижче зліва) об’єм можна обчислити як добуток площі […]...
- Об’єми тіл Геометрія Об’єми тіл Тіло називається Простим, якщойого можна розбити на скінченну кількість трикутних пірамід. Для простих тіл об’єм – це додатна величина, числове значення якої має такі властивості: 1. Рівні тіла мають рівні об’єми. 2. Якщо тіло розбито на частини, які є простими тілами, то об’єм цього тіла дорівнює сумі об’ємів його частин. 3. Об’єм […]...
- Вписана та описана сфера 1. Нехай О А – радіус кулі, ОА = 1 см. АВ = ΚΚ1 = 2ОА = 2 см. CD = 2СО = 2 см. Sбіч. = PKLMN× КК1 = 4 × 2 × 2 = 16 (см2). Відповідь: 16 см2. 2. Нехай АВ =AD = ВВ1 = а. З ΔABD: З ΔΒ1BD: В1D2 = […]...
- Коло, описане навколо трикутника Урок № 49 Тема. Коло, описане навколо трикутника Мета: домогтися засвоєння учнями: – означення кола, описаного навколо трикутника; – властивостей вершин трикутника, вписаного в коло; – змісту теореми про коло, описане навколо трикутника, та схеми її доведення; – наслідку з теореми. Сформувати вміння: – відтворювати формулювання означення та теореми про коло, описане навколо трикутника; – […]...
- Урок 19. Обертання Землі навколо своєї осі та Сонця. Сонячні й місячні затемнення Урок 19. Обертання Землі навколо своєї осі та Сонця. Сонячні й місячні затемнення Мета: поглибити систему знань учнів про Всесвіт шляхом вивчення видів руху Землі і пов’язаних з цим явищ; ознайомити учнів з будовою і призначенням приладу телурій і навчити їх проводити досліди з використанням цього приладу; сформувати в учнів первинні навички дослідницької роботи. Обладнання: […]...
- ПИСЬМОВЕ ДІЛЕННЯ ІМЕНОВАНИХ ЧИСЕЛ НА ЧИСЛО. ЦИЛІНДР ПИСЬМОВЕ ДІЛЕННЯ БАГАТОЦИФРОВОГО ЧИСЛА НА ОДНОЦИФРОВЕ ПИСЬМОВЕ ДІЛЕННЯ ІМЕНОВАНИХ ЧИСЕЛ НА ЧИСЛО. ЦИЛІНДР 702. Виконай ділення з поясненням. 2 695 : 7 25 232 : 8 3 537 : 9 1 848 : 6 703. А) Маса восьми страусів 1 288 кг. Яка маса одного страуса? Б) За одну годину страус може пробігти до 72 […]...
- Зрізаний конус Геометрія Тіла обертання Зрізаний конус Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню – по колу з центром на осі конуса. Така площина відтинає від конуса менший конус. Частина, що залишилась, називається Зрізаним конусом (див. рисунок): ; Зверніть увагу на осьовий переріз зрізаного конуса. Це рівнобічна трапеція, в якої основи – […]...
- ПЛАНЕТА ЗЕМЛЯ. ГЕОГРАФІЧНІ НАСЛІДКИ РУХУ ЗЕМЛІ НАВКОЛО СВОЄЇ ОСІ ТА НАВКОЛО СОНЦЯ. ПРАКТИЧНА РОБОТА 1 “АНАЛІЗ КАРТИ “ГОДИННІ ПОЯСИ” ТА ВИЗНАЧЕННЯ МІСЦЕВОГО ТА ПОЯСНОГО ЧАСУ” УРОК 2. ПЛАНЕТА ЗЕМЛЯ. ГЕОГРАФІЧНІ НАСЛІДКИ РУХУ ЗЕМЛІ НАВКОЛО СВОЄЇ ОСІ ТА НАВКОЛО СОНЦЯ. ПРАКТИЧНА РОБОТА 1 “АНАЛІЗ КАРТИ “ГОДИННІ ПОЯСИ” ТА ВИЗНАЧЕННЯ МІСЦЕВОГО ТА ПОЯСНОГО ЧАСУ” Навчальна мета: повторити, поглибити та систематизувати знання учнів про Землю як космічне тіло та наслідки її рухів у космічному просторі; сформувати первинні практичні уміння працювати з тематичними картами […]...
- Ознака паралельності прямих Геометрія Стереометрія Ознака паралельності прямих Теорема. Дві прямі, паралельні третій прямій, паралельні між собою. Із цієї теореми випливає, що середини сторін просторового чотирикутника (див. рисунок) є вершинами паралелограма (вершини просторового чотирикутника не лежать в одній площині). Зверніть увагу: якщо ABCD – просторовий чотирикутник, то його діагоналі AC і BD – мимобіжні прямі....
- Правильні многокутники Геометрія Многокутники Правильні многокутники Опуклий многокутник називається Правильним, якщо в нього всі сторони рівні й усі кути рівні. Многокутник називається Вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається Описаним навколо кола, якщо всі його сторони дотикаються до деякого кола. Теорема 1. Правильний опуклий многокутник є вписаним у коло й описаним […]...
- Описана піраміда Геометрія Комбінації геометричних тіл Описана піраміда Якщо вершина піраміди проектується в центр кола, яке є вписаним в основу піраміди, то центр вписаної кулі – точка перетину висоти піраміди з бісектрисою лінійного кута двогранного кута при ребрі основи. У будь-яку правильну піраміду можна вписати кулю, центр якої лежить на висоті піраміди. Точки дотику кулі й бічних […]...