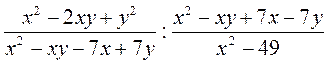Ділення дробів
Урок № 16
Тема. Ділення дробів
Мета: закріпити знання учнів про послідовність дій для перетворення частки раціональних дробів у раціональний дріб (алгоритм, вивчений на попередньому уроці); відпрацювати вміння застосовувати алгоритм для перетворення частки раціональних дробів у раціональний дріб; удосконалити вміння виконувати скорочення раціональних дробів, а також перетворення суми, різниці, добутку раціональних дробів та степеня раціонального дробу в раціональний дріб із використанням вивчених раніше алгоритмів.
Тип уроку:
Наочність та обладнання: опорний конспект “Множення та ділення дробів. Піднесення дробу до степеня”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
За необхідності можна організувати перевірку за зразком (якщо на попередньому уроці були труднощі із виконанням ділення за складеним алгоритмом) або провести роботу у формі “Знайди помилку”.
III. Формулювання мети і завдань уроку
За умови наявності в учнів розуміння схеми вивчення будь-якого предмета (розуміння змісту основних теоретичних питань > знання цих понять > формування вміння
IV. Актуалізація опорних знань та вмінь
@ Відповідно до мети уроку слід активізувати такі знання і вміння учнів: виконання арифметичних дій із раціональними числами; тотожні перетворення цілих виразів (перетворення цілого виразу в многочлен, розкладання многочленів на множники), а також перетворення раціональних дробів, вивчених на попередніх уроках.
Виконання усних вправ
1. Обчисліть: 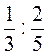 ;
; 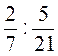 ;
; 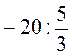 ;
; 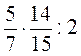 ;
; 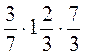 .
.
2. Назвіть вираз, обернений до виразу: 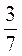 ; 13;
; 13; 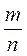 ;
; 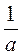 ; а + 1;
; а + 1; 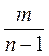 ; -5с2;
; -5с2; 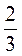 (а + b).
(а + b).
3. Подайте у вигляді дробу вираз: а) 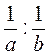 ; б)
; б) 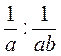 ; в)
; в) 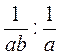 ; г)
; г) 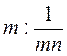 ; д)
; д) 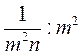 ; є)
; є) 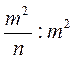 .
.
4. Розкладіть на множники вираз:
A) 3a – 6b; б) 3a – ab; в) 3а – 3а2; г) mх – m; д) a2 + b2 + 2ab; е) m2 – 8m; ж) m3 – 8; з) b3 – 4m; и) m3 – 4m2 + 4b; к) m3 – m2 + m – 1.
V. Застосування знань
@ Як було сказано вище (урок 15), зазвичай алгоритм ділення раціональних дробів учні засвоюють досить легко. Тому, за умови сформованих умінь виконання множення раціональних дробів та виконання скорочення раціональних дробів, засвоєнню сталих умінь виконувати перетворення частки раціональних дробів нічого не заважає. У такому випадку на поточному уроці можна приділити увагу розв’язуванню вправ на виконання ділення разом із множенням раціональних дробів та деяким способам раціональних перетворень частки і добутку раціональних дробів. Приклади таких перетворень (разом із коментарем) складатимуть зміст нового матеріалу, винесеного на урок, тому мають бути записані в зошити учнів як опорні.
VI. Удосконалення вмінь
Виконання усних вправ
1. Подайте вирази у вигляді дробу:
А) 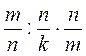 ; б)
; б) 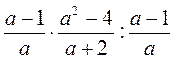 ; в)
; в) 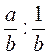 ; г)
; г) 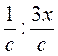 ; д)
; д) 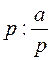 ; є)
; є) 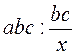 ; ж)
; ж) 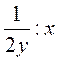 ; з)
; з) 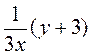 .
.
2. Петрик Тяпляпкін записав два алгебраїчних дроби. Коли він перший дріб розділив на другий, то дістав 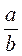 , а коли другий дріб розділив на перший,
, а коли другий дріб розділив на перший, 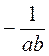 . Чи не помилився він?
. Чи не помилився він?
3. При деякій парі значень а і b вираз 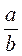 = 5. Чому дорівнюють при тому самому значенні а і b значення виразів:
= 5. Чому дорівнюють при тому самому значенні а і b значення виразів:
А) 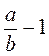 ; б)
; б) 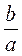 ; в)
; в) 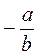 ; г)
; г) 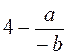 ; д)
; д) 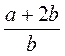 ?
?
Виконання письмових вправ
@ Як і на всіх попередніх уроках, через систему усних і письмових вправ продовжується робота з відпрацювання таких навичок учнів: перетворення суми, різниці та добутку раціональних дробів у раціональний дріб та виконання скорочення раціональних дробів із використанням різних видів перетворень виразів (вивчених у 7 класі).
Вправи, запропоновані для розв’язування на уроці, мають сприяти подальшому формуванню вмінь учнів виконувати перетворення частки, добутку, суми і різниці раціональних дробів (різного рівня складності) із використанням як вивчених алгоритмів, так і деяких прийомів раціонального виконання дій.
Для реалізації дидактичної мети уроку слід розв’язати завдання такого змісту.
1. Перетворення частки двох раціональних дробів (раціонального дробу і цілого виразу) у раціональний дріб. 1) Спростіть вираз:
А) 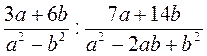 ; б)
; б) 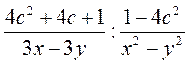 ; в)
; в) 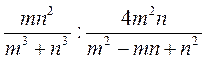 ; г)
; г) 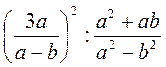 ; д)
; д) 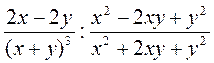 ; є)
; є) 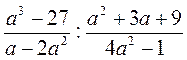 .
.
2) Виконайте ділення:
А) 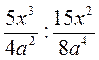 ; б)
; б) 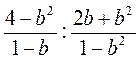 ; в)
; в) 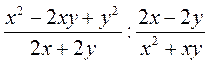 .
.
2. Знаходження значень виразу зі змінною (змінними), що має вигляд частки раціональних дробів, при даному значенні змінної (змінних), попередньо подавши його у вигляді раціонального дробу.
Знайдіть значення виразу 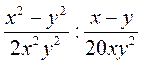 при х =
при х = 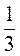 ; у = 2
; у = 2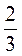 .
.
3. Спрощення виразів, що містять ділення, множення раціональних дробів та піднесення раціонального дробу до степеня.
Спростіть вираз 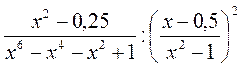 .
.
4. Перетворення суми (або різниці) раціональних дробів на раціональний дріб.
Виконайте дії: 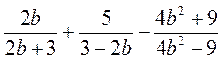 .
.
5. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Доведіть, що вираз 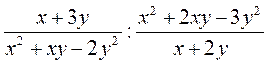 Набуває лише додатних значень.
Набуває лише додатних значень.
2) Який вираз пропущений?
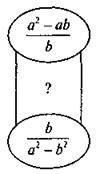
VII. Підсумки уроку
Самостійна робота № 4
(Можна провести її як домашню самостійну роботу)
Варіант 1 | Варіант 2 |
Подайте у вигляді дробу: | |
А°) Б-) В-) Г-) Д–) Є–) | А°) Б-) В-) Г-) Д–) Є–) |
VIII. Домашнє завдання
1. Повторити алгоритми виконання арифметичних дій із раціональними дробами та алгоритм скорочення раціональних дробів (див. конспекти попередніх уроків).
2. Виконати вправи на застосування цих алгоритмів (зміст вправ відповідає змісту вправ класної роботи).
3. Повторити: зміст понять раціональний вираз та раціональний дріб (скласти кілька прикладів та контрприкладів), правило послідовності виконання арифметичних дій у числових виразах (див. довідник, 5 клас), виконати вправи на застосування цього правила (приклад на кілька арифметичних дій у числовому виразі).
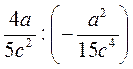 ;
;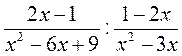 ;
;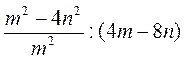 ;
;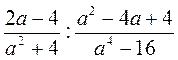 ;
;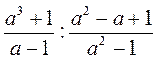 ;
;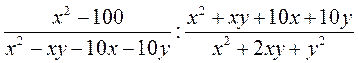
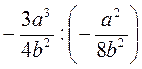 ;
;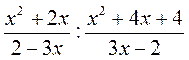 ;
;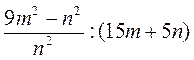 ;
;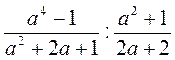 ;
;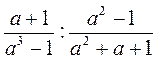 ;
;