Головна ⇒ 📌Довідник з математики ⇒ Додатні та від’ємні числа
Додатні та від’ємні числа
Математика – Алгебра
Раціональні числа
Додатні та від’ємні числа
Координатна пряма
Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається Координатною прямою.
Число, що показує положення точки на координатній прямій, називається Координатою точки.
Приклад
Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це означає, що координата точки А – число 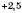 . Позначається: А (2,5).
. Позначається: А (2,5).

Точка B на рисунку розташована ліворуч від 0 на відстані 4 одинакових відрізків. Позначається: B
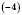 .
.Отже, числа зі знаком “+” називають Додатними. При записі додатних чисел знак “+”, як правило, опускають.
Числа зі знаком “–” називають Від’ємними.
Число 0 не є ні додатним, ні від’ємним. Два числа, що відрізняються одне від одного лише знаком, називаються Протилежними числами.
Число, протилежне числу а, позначають
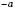 . Таким чином, якщо
. Таким чином, якщо 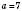 , то
, то 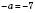 ; якщо
; якщо 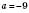
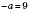 , тобто
, тобто 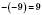 . Число 0 протилежне саме собі:
. Число 0 протилежне саме собі: 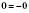 . Якщо дане число додатне, то протилежне йому – від’ємне і навпаки.
. Якщо дане число додатне, то протилежне йому – від’ємне і навпаки.Зверніть увагу, що за записом
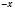 не можна сказати, яке це число – додатне чи від’ємне.
не можна сказати, яке це число – додатне чи від’ємне.Якщо х – додатне, то
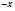 – від’ємне; якщо х – від’ємне, то
– від’ємне; якщо х – від’ємне, то 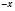 – додатне; якщо
– додатне; якщо 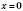 , то
, то 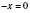 .
.Натуральні числа, протилежні їм числа і число 0 називаються Цілими числами. Числа, які можна записати у вигляді дробу
 , де m – ціле число, а n – натуральне число, називають Раціональними числами.
, де m – ціле число, а n – натуральне число, називають Раціональними числами.Кожне раціональне число можна записати у вигляді скінченного або нескінченного періодичного десяткового дробу.
Related posts:
- Протилежні числа. Цілі числа. Раціональні числа Розділ 4 Раціональні числа і дії мідними §35. Протилежні числа. Цілі числа. Раціональні числа Точки A і B з відповідними координатами 2 і -2 однаково віддалені від початку відліку – точки О і знаходять ся по різні боки від неї (мал. 71). Щоб потрапити з точки О в точки A(2) і B(-2), треба відкласти однакові […]...
- ДОДАТНІ ТА ВІД’ЄМНІ ЧИСЛА. ЧИСЛО НУЛЬ Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ У розділі дізнаєтесь: Ü про додатні та від’ємні числа; Ü що таке координатна пряма; Ü що таке модуль числа; Ü які числа називаються цілими; Ü що таке раціональні числа; Ü як порівнювати раціональні числа; Ü як виконувати арифметичні дії з раціональними числами; Ü як застосувати вивчений матеріал […]...
- Додатні і від’ємні числа. Число 0 Урок № 6 2 Тема. Додатні і від’ємні числа. Число 0 Мета: сформувати уявлення учнів про зміст понять “додатні числа”, “від’ємні числа”, а також виробити вміння відрізняти ці види чисел і виконувати прості вправи, що передбачають таку класифікацію. Тип уроку: засвоєння нових знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Обчисліть: А) Б) […]...
- Додатні та від’ємні числа. Число 0 Розділ 4 Раціональні числа і дії мідними У цьому розділі ви: – згадаєте поняття рівняння; – ознайомитеся з поняттями додатного, від’ємного та раціонального чисел; – дізнаєтеся про координатну пряму, модуль числа; – навчитеся порівнювати та виконувати дії з додатними та від’ємними числами, розв’язувати нові види рівнянь. §33. Додатні та від’ємні числа. Число 0 З повідомлень […]...
- Протилежні числа Урок № 6 4 Тема. Протилежні числа Мета: сформувати уявлення про зміст поняття “протилежні числа”; навчити знаходити й записувати число, протилежне до даного, розв’язувати рівняння, що передбачають застосування поняття числа, протилежного до даного. Тип уроку: засвоєння вмінь та навичок. Хід уроку І. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Запишіть число “мінус три” […]...
- МОДУЛЬ ЧИСЛА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 23. МОДУЛЬ ЧИСЛА Позначимо на координатній прямій точки А (-6), В (-2) і С (2) (мал. 104). Яка точка розміщена найдалі від початку відліку О? Точка А, оскільки ОА = б од., а ОВ = ОС = 2 од. Мал. 104 Порівнюючи відстані від точок А, […]...
- Застосування модуля числа. Відстань між точками на координатній прямій Урок № 6 7 Тема. Застосування модуля числа. Відстань між точками на координатній прямій Мета: поглибити знання учнів про властивості модуля раціонального числа та відпрацювати навички застосування означення та властивостей модуля для розв’язування рівнянь та нерівностей. Тип уроку: застосування знань, умінь і навичок Хід уроку I. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. […]...
- Цілі числа, раціональні числа Урок № 6 5 Тема. Цілі числа, раціональні числа Мета: узагальнити і систематизувати відомості учнів про види чисел; домогтися засвоєння поняття “ціле число”, “раціональне число” і зв’язок між ними; навчити класифікувати числа. Тип уроку: узагальнення і систематизація знань. Хід уроку І. Перевірка домашнього завдання (вибірково у “слабких” перевіряємо зошити) Математичний диктант Варіант 1 [2] 1. […]...
- Геометричні фігури, точка, пряма, промінь Розділ 1. Елементарні геометричні фігури та їхні властивості § 1. Геометричні фігури, точка, пряма, промінь 1. 1) Прямій а належать точки А, В, С. 2) Прямій b належать точки Р i В. 3) Прямій а і прямій b належить точка В. 4) Точки А і С належать прямій а, але не належать прямій b. 5) […]...
- ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 24. ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА У п’ятому класі ви вивчали натуральні числа. Це числа, які використовують для лічби: 1; 2; 3; 4; … . Усі натуральні числа утворюють множину натуральних чисел. Цю множину позначають буквою N. Множина N має нескінченно багато елементів, оскільки натуральних чисел нескінченно […]...
- ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА ЗАДАЧІ НА ПОВТОРЕННЯ ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА 1. Скільки чисел натурального ряду розміщено між числами: 1)120 і 129; 2) 999 і 1100; 3)8901 і 8910; 4) 50000 і 50020? 2. На прямій дано три точки А, В і С. Знайдіть довжину відрізка ВС, якщо АВ = 8 см і АС – 9 см. Скільки розв’язків […]...
- Раціональні числа; порівняння, додавання та віднімання. Розв’язування вправ Урок № 7 8 Тема. Раціональні числа; порівняння, додавання Та віднімання. Розв’язування вправ Мета: підготувати учнів до виконання тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь і навичок. Хід уроку I. Перевірка домашнього завдання @ Якщо на попередньому уроці не встигли зробити, то на початку цього уроку ми проводимо тестову роботу (з теми […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Модуль раціонального числа Урок № 6 6 Тема. Модуль раціонального числа Мета: сформувати уявлення учнів про геометричний зміст поняття “модуль числа”; виробити вміння читати, записувати вирази, що містять модуль, а також знаходити значення виразів, що містять числа під знаком модуля. Тип уроку: засвоєння нових знань і вмінь Хід уроку І. Перевірка домашнього завдання Усні вправи 1. Обчисліть А) […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
- Точки, прямі, промені Розділ 1. Найпростіші геометричні фігури та їх властивості § 1. Точки, прямі, промені 1. 1) Прямій m належать точки: В, D, N; 2) на прямій m не лежать точки: М, А, С. Відповідь: В є m, D є m, N є m, М ∉ m, A ∉ m, С ∉ m. 2. Відповідь: пряма АВ […]...
- ДІЛЬНИКИ і КРАТНІ НАТУРАЛЬНОГО ЧИСЛА. ПРОСТІ ЧИСЛА Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ У розділі дізнаєтесь: – що таке дільники і кратні натурального числа; – які є ознаки подільності чисел; – які числа називаються простими та як їх знаходити; – як розкласти число на множники; – що таке найбільший спільний дільник чисел та як його знаходити; – що таке найменше спільне кратне чисел […]...
- Лінійна функція Розв’яжіть задачі 882. мал. 40. 883. 1) ні; 2) ні; 3) так. 884. 1) так; 2) ні; 3)так. 885. 1) ні; 2) ні; 3) так. 886. 1) ні; 2) ні; 3) так. 887. 1) ні; 2) ні; 3) так. 888. 1) 4; 2) -6; 3) 2/3. 889. 1) 3; 2) -0,5; 3) %. 890. 1) […]...
- Прості та складені числа Розділ 1 Подільність натуральних чисел §4. Прості та складені числа Число 11 ділиться тільки на 1 і на себе. Іншими словами, число 11 має тільки два дільники: 1 і 11. У числа 8 чотири дільники: 1, 2, 4 і 8. Число 18 має шість дільників: 1, 2, 3, 6, 9 і 18. Такі числа, як […]...
- Модуль числа Математика – Алгебра Раціональні числа Модуль числа Відстань від початку відліку до точки, що зображає число на координатній прямій, називається Модулем даного числа. Позначення: – модуль а. Очевидно, що для додатних чисел і 0 , для від’ємних . для будь-якого числа а. Модулі протилежних чисел рівні: . Приклади 1) ; ; . 2) Розв’яжіть рівняння. […]...
- ЧИСЛО І ЦИФРА 6. УТВОРЕННЯ ЧИСЛА ПРИЛІЧУВАННЯМ 1. ПОНЯТТЯ “ШОСТИЙ”. “СУСІДИ” ЧИСЛА. СКЛАД ЧИСЛА 6. НАПИСАННЯ ЦИФРИ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 23. ЧИСЛО І ЦИФРА 6. УТВОРЕННЯ ЧИСЛА ПРИЛІЧУВАННЯМ 1. ПОНЯТТЯ “ШОСТИЙ”. “СУСІДИ” ЧИСЛА. СКЛАД ЧИСЛА 6. НАПИСАННЯ ЦИФРИ 6 Мета: ознайомити учнів з утворенням числа б прилічуванням та цифрою 6, з поняттям “шостий”; вчити називати “сусідів” числа, склад числа б, писати […]...
- Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Урок № 37 Тема. Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Мета: систематизувати, узагальнити знання учнів щодо поняття числа та видів чисел, сформувати уявлення про множину дійсних чисел; сформувати вміння учнів відтворювати означення та властивості видів чисел, вивчених на уроці, виконувати найпростіші дії з дійсними числами (зокрема порівняння), використовувати вивчені властивості […]...
- ПОВТОРЕННЯ. ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА Цілі: – навчальна: повторити поняття натурального числа; відтворити вміння читати, записувати і порівнювати натуральні числа; повторити поняття прямої, відрізка, променя, кута, види кутів; – розвивальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип уроку: узагальнення та систематизація знань. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ____________________________________________ ____________________________________________ […]...
- ПОРІВНЯННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 25. ПОРІВНЯННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Із порівнянням раціональних чисел ви зустрічаєтесь чи не щодня. Наприклад, узимку, коли надворі мороз -15°, про температуру повітря кажуть, що вона менша від нуля: -15° < 0°. У відлигу, коли повітря прогрілося до +5°, кажуть, що температура стала більшою за нуль: +5° […]...
- Натуральні числа і дії над ними Математика – Алгебра Натуральні числа і дії над ними Числа, які використовуються при лічбі предметів, називаються Натуральними числами. Натуральний ряд чисел є нескінченним. Він записується так: 1, 2, 3, … 0 не є натуральним числом. Зазвичай прийнято користуватись Позиційною десятковою системою числення. Тобто кожне число може бути записане за допомогою десяти цифр (0, 1, 2, […]...
- Промінь, пряма, площина Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 17. Промінь, пряма, площина Продовжимо відрізок АВ за допомогою лінійки за точку В (рис. 38). На рисунку таке продовження обмежене розмірами аркуша, але можна уявити, що ми продовжили відрізок необмежено. Якщо продовжити відрізок АВ за його кінець В необмежено, то одержимо промінь […]...
- ЧИСЛА І ЦИФРИ. ОДНОЦИФРОВІ ЧИСЛА. СКЛАДАННЯ ПРИКЛАДІВ ЗА ЧИСЛОВИМИ ПРОМЕНЯМИ. ПОРІВНЯННЯ ЧИСЕЛ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 34. ЧИСЛА І ЦИФРИ. ОДНОЦИФРОВІ ЧИСЛА. СКЛАДАННЯ ПРИКЛАДІВ ЗА ЧИСЛОВИМИ ПРОМЕНЯМИ. ПОРІВНЯННЯ ЧИСЕЛ Мета: ознайомити учнів з поняттям “одноцифрові числа”; узагальнити поняття “число” і “цифра”; учити порівнювати числа, складати приклади за числовими променями; розвивати мислення; виховувати інтерес до математики. Хід уроку […]...
- Дійсні числа Математика – Алгебра Квадратні корені Раціональні числа – це числа, які можуть бути записані у вигляді , де m – ціле число, n – натуральне. Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. І навпаки, кожний нескінченний періодичний десятковий дріб є раціональним числом. Числа, які зображуються нескінченними неперіодичними десятковими дробами, називають ірраціональними. […]...
- Точка та прямі § 1. Найпростіші геометричні фігури та їхні властивості 1. Точка та прямі Практичні завдання 1. 2. Прямі ME, МК, ЕК, EM, КМ, КЕ. 3. Точка С належить прямій а, точка С належить прямій b. 4. Утворилося три прямих. 5. 6. Можна отримати три або одну точку перетину. 7. 1) 2) 3) Вправи 8. 1) Прямій […]...
- ЧИСЛО І ЦИФРА 5. УТВОРЕННЯ ЧИСЛА ПРИЛІЧУВАННЯМ 1. ПОНЯТТЯ “П’ЯТИЙ”. КІЛЬКІСНА І ПОРЯДКОВА ЛІЧБА. “СУСІДИ” ЧИСЛА. НАПИСАННЯ ЦИФРИ 5 ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 20. ЧИСЛО І ЦИФРА 5. УТВОРЕННЯ ЧИСЛА ПРИЛІЧУВАННЯМ 1. ПОНЯТТЯ “П’ЯТИЙ”. КІЛЬКІСНА І ПОРЯДКОВА ЛІЧБА. “СУСІДИ” ЧИСЛА. НАПИСАННЯ ЦИФРИ 5 Мета: ознайомити учнів з утворенням числа 5 і цифрою 5; вчити писати цифру 5, порівнювати числа в межах 5; вправляти учнів […]...
« МЕЛАНІЗМ