Елементи комбінаторики
Математика – Алгебра
Елементи комбінаторики
Поняття Множини належить до первісних понять математики, якому не дається означення.
Позначення: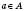 
(елемент належить множині A); 
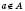(елемент не належить множині A); 
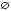– порожня множина, яка не містить жодного елемента.
Дві множини називаються Рівними, якщо вони складаються з тих самих елементів.
Якщо множина B складається з деяких елементів множини A (і тільки з них), то множина B називається Підмножиною
Позначення:
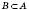.Перерізом множинA і B називається множина C, яка складається з усіх тих, і тільки тих елементів, які належать кожній із даних множин.
Позначення:
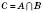.Об’єднанням (або сумою) двох множин A і B називається така множина C, яка складається з усіх елементів множин A і B, і тільки з них.
Позначення:
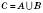.Різницею двох множин A і B називається така множина С, яка складається з усіх елементів множини A, які не належать множині B.
Позначення:
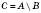.На рисунку зображено переріз, об’єднання
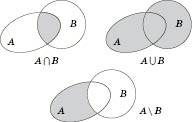
У випадку, коли
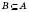, різниця 
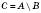називається Доповненням множини B Щодо множиниA.Скінченні множини, для яких установлений порядок елементів, називають Упорядкованими.
Указати порядок розташування елементів у скінченній множині з n елементів означає поставити у відповідність кожному елементу множини певне натуральне число від 1 до n.
Будь-яка впорядкована множина, яка складається з n елементів, називається Перестановкою з N елементів. Число перестановок з n елементів позначається
. 
. 
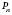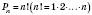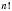– це добуток усіх натуральних чисел від 1 до n включно.Розміщенням з M елементів поN називається будь-яка впорядкована множина з n елементів даної множини M, яка містить m елементів, де
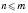.Позначення:
.
;
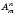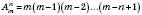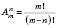.Комбінацією з M елементів поN називається будь-яка підмножина з n елементів даної множини M, яка містить m елементів, де
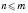.Позначення:
.
; 
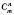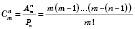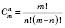.Властивості числа комбінацій:
1.
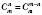.2.
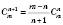.3.
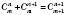.4.
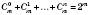.Біном (двочлен) – вираз вигляду
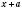.Формула бінома Ньютона:
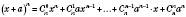.Права частина цієї формули називається Розкладом бінома.
Властивості розкладу бінома Ньютона:
1. Кількість членів розкладу бінома на одиницю більша, ніж показник степеня бінома.
2. Усі члени розкладу мають один і той самий степінь n як суму показників степенів x і a.
Кожний рядок цього трикутника – набір біноміальних коефіцієнтів для розкладу відповідного степеня.