Графіки тригонометричних функцій
Математика – Алгебра
Тригонометричні функції
Графіки тригонометричних функцій
Для побудування графіків тригонометричних функцій візьмемо 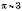 . Побудуємо графік функції
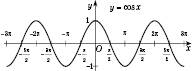
. Побудуємо графік функції 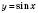 (див. рисунок).
(див. рисунок).
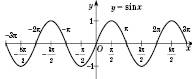
Ця крива називається синусоїдою.
Графік функції 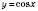 можна дістати з графіка функції
можна дістати з графіка функції 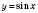 паралельним перенесенням його вліво вздовж осі Ox на
паралельним перенесенням його вліво вздовж осі Ox на 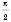 одиниць. Це випливає з формули
одиниць. Це випливає з формули
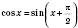 .
.
Побудуємо графік функції
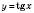 :
: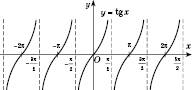
Зверніть увагу: значення
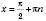 ,
, 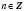 , не входять до області визначення функції
, не входять до області визначення функції 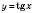 . Прямі
. Прямі 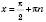 ,
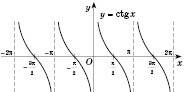
, 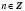 , є асимптотами графіка. Графік носить назву Тангенсоїди.
, є асимптотами графіка. Графік носить назву Тангенсоїди.Графік функції
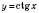 легко дістати, скориставшись формулою зведення
легко дістати, скориставшись формулою зведення 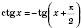 :
:
Розглянемо графік
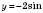
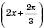 .
.Запишемо функцію у вигляді
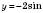
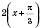 .
.Із цього випливає, що графік цієї функції можемо дістати, якщо побудувати:
1) графік функції
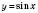 ;
;2) графік функції
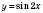 , стискаючи графік функції
, стискаючи графік функції 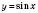 у два рази до оcі Oy;
у два рази до оcі Oy;3) графік функції
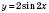 , розтягуючи у два рази вздовж осі Oy графік функції
, розтягуючи у два рази вздовж осі Oy графік функції 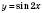 ;
;4) графік функції
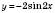 , відображуючи графік функції
, відображуючи графік функції 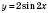 симетрично відносно осі Ox;
симетрично відносно осі Ox;5) графік функції
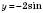
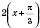 , паралельно переносячи графік
, паралельно переносячи графік 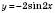 на відстань
на відстань 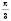 вліво вздовж осі Ox.
вліво вздовж осі Ox.На рисунку не показані поступові перетворення графіка, а тільки остаточний вигляд графіка функції
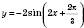 :
: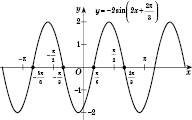
Зверніть увагу: на практиці можна відразу побудувати графік функції
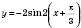 , якщо врахувати такі міркування:
, якщо врахувати такі міркування:1) графік матиме вигляд синусоїди;
2) точка графіка
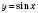 з координатами (0; 0) перейде в шуканому графіку в точку
з координатами (0; 0) перейде в шуканому графіку в точку 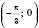 ;
;3) період функції
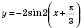 дорівнює
дорівнює  ;
;4) максимальні й мінімальні значення функції
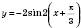 відповідно дорівнюватимуть 2 і –2;
відповідно дорівнюватимуть 2 і –2;5) синусоїда
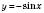 симетрична синусоїді
симетрична синусоїді 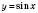 відносно осі Оx.
відносно осі Оx.Таким чином, при зростанні значень аргументу від
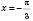 до нескінченності з кроком
до нескінченності з кроком 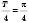 функція набуватиме значення 0; –2; 0; –2; 0… і т. д.
функція набуватиме значення 0; –2; 0; –2; 0… і т. д.Аналогічно можна міркувати, якщо треба побудувати графіки функцій:
y = Acos(kx+b);
y = Atg(kx+b);
y = Actg(kx+b).
Величини, які змінюються за законом
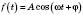 або
або 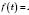
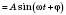 , називаються Гармонічними коливаннями.
, називаються Гармонічними коливаннями.При цьому: A – амплітуда коливання;
 – циклічна частота коливання;
– циклічна частота коливання; 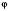 – початкова фаза коливання.
– початкова фаза коливання.Період функції
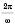 – Період гармонічного коливання.
– Період гармонічного коливання.