ГРАФІКИ ШЛЯХУ І ШВИДКОСТІ
Розділ ІІ Механічний рух
& 14. ГРАФІКИ ШЛЯХУ І ШВИДКОСТІ
Визначення шляху на графіку швидкості
У фізиці й математиці використовують три способи подання інформації про зв’язок між різними величинами: а) у вигляді формули, наприклад, s =v ∙ t; б) у вигляді таблиці; в) у вигляді графіка (малюнка).
Залежність швидкості від часу v(t) – графік швидкості, зображається за допомогою двох взаємно перпендикулярних осей. Уздовж горизонтальної осі відкладатимемо час, а вздовж вертикальної – швидкість (мал. 14.1). Треба завчасно продумати
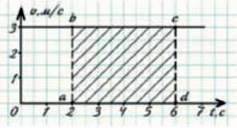
Мал. 14.1. Графік швидкості тіла, що рівномірно рухається зі швидкістю 3 м/с. Шлях, пройдений тілом з 2-ї по 6-ту секунди,
Зображення рівномірного руху таблицею і графіками
Розглянемо рівномірний рух тіла
 . Ви вже знаєте, що інформацію про залежність однієї величини від іншої можна подавати у вигляді таблиці (масиву, як кажуть в інформатиці):
. Ви вже знаєте, що інформацію про залежність однієї величини від іншої можна подавати у вигляді таблиці (масиву, як кажуть в інформатиці):T, c | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
V, м/с | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
Із таблиці видно, що в усі вказані моменти часу швидкість дорівнює 3 м/с. Нехай масштаб осі часу 2 кл. = 1 с, а осі швидкості 2 кл. = 1 м/с. Графік залежності швидкості від часу (скорочено кажуть: графік швидкості) наведено на малюнку 14.1.
За допомогою графіка швидкості можна знаходити шлях, який тіло проходить за певний інтервал часу. Для цього треба зіставити два факти: з одного боку, шлях можна знайти, помноживши швидкість на час, а з іншого – добуток швидкості на час, як видно із малюнка – це площа прямокутника зі сторонами t і v.
Наприклад, з другої до шостої секунди тіло рухалося упродовж чотирьох секунд і пройшло 3 м/с ∙ 4 с = 12 м. Це площа прямокутника аbсd, довжина якого дорівнює 4 с (відрізок ad вздовж осі часу) і висота 3 м/с (відрізок аb вздовж вертикалі). Площа, щоправда, дещо незвична, оскільки вимірюється не в м2, а в м. Отже, площа під графіком швидкості чисельно дорівнює пройденому шляху.
Графік шляху
Графік шляху s(t) можна зобразити, використовуючи формулу s = v ∙ t, тобто в нашому випадку, коли швидкість становить 3 м/с: s = 3 ∙ t. Побудуємо таблицю:
T, с | 0 | 1 | 2 | 3 | 4 | 5 |
S, м | 0 | 3 | 6 | 9 | 12 | 15 |
Уздовж горизонтальної осі знову відкладають час (t, с), а вздовж вертикальної – шлях. Біля осі шляху пишемо: s, м (мал. 14.2).
Визначення швидкості на графіку шляху
Зобразимо тепер на одному малюнку два графіки, які відповідатимуть рухам зі швидкостями 3 м/с (пряма 2) і 6 м/с (пряма 1) (мал. 14.3). Видно, що чим більша швидкість тіла, тим крутіша лінія точок графіка.
Існує й обернена задача: маючи графік руху, потрібно визначити швидкість і записати рівняння шляху (мал. 14.3). Розглянемо пряму 2. Від початку руху і до моменту часу t = 2 с тіло пройшло шлях s = 6 м. Отже, його швидкість: v = 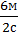 = 3
= 3  . Вибір іншого інтервалу часу нічого не змінить, наприклад, на момент t = 4 с шлях, пройдений тілом від початку руху, становить s = 12 м. Відношення знову дорівнює 3 м/с. Але так і повинно бути, оскільки тіло рухається зі сталою швидкістю. Тому найпростіше було б вибрати інтервал часу 1 с, адже шлях, пройдений тілом за одну секунду, чисельно дорівнює швидкості. Шлях, пройдений першим тілом (графік 1) за 1 с, дорівнює 6 м, тобто швидкість першого тіла дорівнює 6 м/с. Відповідні залежності шляху від часу у цих двох тіл будуть:
. Вибір іншого інтервалу часу нічого не змінить, наприклад, на момент t = 4 с шлях, пройдений тілом від початку руху, становить s = 12 м. Відношення знову дорівнює 3 м/с. Але так і повинно бути, оскільки тіло рухається зі сталою швидкістю. Тому найпростіше було б вибрати інтервал часу 1 с, адже шлях, пройдений тілом за одну секунду, чисельно дорівнює швидкості. Шлях, пройдений першим тілом (графік 1) за 1 с, дорівнює 6 м, тобто швидкість першого тіла дорівнює 6 м/с. Відповідні залежності шляху від часу у цих двох тіл будуть:
S1 = 6 ∙ t і s2 =3 ∙ t.
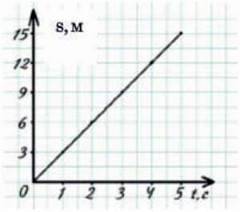
Мал. 14.2. Графік шляху. Решта точок, крім шести, вказаних у таблиці, поставлені в приміщені, що рух упровдож всього часу був рівномірним
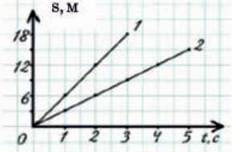
Мал. 14.3. Графік шляху у випадку різних швидкостей
Підведемо підсумки
– У фізиці використовують три способи подачі інформації: графічний, аналітичний (формулами) і таблицею (масивом). Третій спосіб більш пристосований для розв’язання на комп’ютері.
– Шлях чисельно дорівнює площі під графіком швидкості.
– Чим крутіший графік s(t), тим більша швидкість.
Творчі завдання
14.1. Накресліть графіки швидкості і шляху, коли швидкість тіла рівномірно збільшується, або зменшується.
Вправа 14
1. Як визначають шлях на графіку швидкості?
2. Чи можна записати формулу для залежності шляху від часу, маючи графік s(t)?
3. Чи зміниться кут нахилу графіку шляху, якщо масштаб на осях зменшити вдвічі?
4. Чому графік шляху рівномірного руху зображається прямою?
5. Яке з тіл (мал. 14.4) має найбільшу швидкість?
6. Назвіть три способи подання інформації про рух тіла, а також (на вашу думку) їхні переваги й недоліки.
7. Як можна визначити шлях за графіком швидкості?
8. а) Чим відрізняються графіки шляху для тіл, що рухаються з різними швидкостями? б) Що в них спільного?
9. За графіком (мал. 14.1) знайдіть шлях, пройдений тілом від початку першої до кінця третьої секунди.
10. Який шлях пройшло тіло (мал. 14.2) за: а) дві секунди; б) чотири секунди? в) Укажіть, де починається третя секунда руху, і де вона закінчується.
11. Зобразіть на графіках швидкості та шляху рух зі швидкістю а) 4 м/с; б) 2 м/с.
12. Запишіть формулу залежності шляху від часу для рухів, зображених на мал. 14.3.
13. а) Знайдіть швидкості тіл за графіками (мал. 14.4); б) запишіть відповідні рівняння шляху й швидкості. в) Побудуйте графіки швидкості цих тіл.
14. Побудуйте графіки шляху й швидкості для тіл, рухи яких задані рівняннями: s1 = 5 ∙ t і s2 = 6 ∙ t. Чому дорівнюють швидкості тіл?
15. За графіками (мал. 14.5) визначте: а) швидкості тіл; б) шляхи, пройдені ними за перші 5 с. в) Запишіть рівняння шляху й побудуйте відповідні графіки для усіх трьох рухів.
16. Накресліть графік шляху для руху першого тіла відносно другого (мал. 14.3).
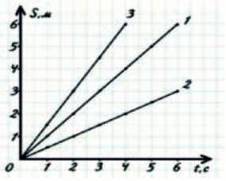
Мал. 14.4.
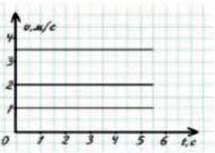
Мал. 14.5.

