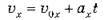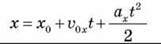Графіки залежності кінематичних величин від часу під час рівномірного прямолінійного руху
1-й семестр
МЕХАНІКА
1. Кінематика
Урок 10/12
Тема. Графіки залежності кінематичних величин від часу під час рівномірного прямолінійного руху
Мета уроку: закріпити навички читання та побудови графіків рухомого тіла при прямолінійному рівноприскореному русі
Тип уроку: закріплення знань
РЕКОМЕНДАЦІЇ ЩОДО ПРОВЕДЕННЯ УРОКУ
Вміння та навички учнів будувати й читати графіки є гарним засобом перевірки рівня усвідомленого засвоєння ними основних понять рівноприскореного руху.
Слід мати на увазі, що учні на уроках
Крім того, у курсі алгебри вивчається квадратний тричлен, що записується у вигляді у = ах2 + bх + с, де в якості незалежної змінної виступає х.
Зіставимо рівняння, що вивчаються під час уроків з математики, з рівняннями руху в кінематиці:
Математика | Фізика |
У = ах + b |
|
У = ах2 + bх + с |
|
Це порівняння сприятиме не тільки актуалізації міжпредметних
Далі необхідно зобразити на дошці кілька графіків, а учні (у свою чергу) повинні спробувати якісно пояснити і визначити характер руху, значення початкової швидкості й прискорення, записати відповідні рівняння руху.
Потім можна запропонувати учням виконати кілька завдань на графіки залежності кінематичних величин від часу.
Задачі, що розв’язуються під час уроку
1. За графіками x(t) і 
X(t) (див. рис.) опишіть рух. Чому відповідають точки А на кожному з рисунків? Запишіть формули X(t) для кожного з рухів.
Розв’язування
На першому рисунку показано графіки прямолінійних рівномірних рухів (X = 0,33 м/с і X = -0,5 м/с). Точка А відповідає моменту зустрічі тіл.
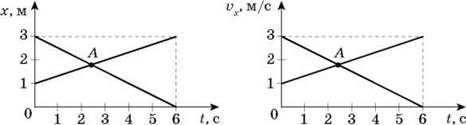
На другому рисунку – графіки прямолінійного рівноприскореного руху (X = 1 + 0,33t і X = 3 – 0,5t). Точка А на цьому рисунку відповідає моменту, коли швидкості обох тіл однакові.
2. Прямолінійний рівноприскорений рух описується формулою х = -4 + 2t – t2. Опишіть рух і побудуйте до нього графіки X(t), sx(t), l(t).
Розв’язування
Оскільки формула x(t) являє собою окремий випадок загальної формули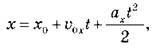 
рух є прямолінійним рівноприскореним, причому х0 = -4 м, 0х = 2 м/с, ах = -2 м/с2. Таким чином, за першу секунду швидкість тіла зменшилася від 2 м/с до нуля, а потім тіло рухалося в протилежному напрямі осі Ох, причому модуль його швидкості збільшувався. Залежності швидкості й переміщення від часу задаються формулами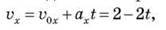 
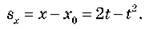Графіки цих залежностей наведені на рисунку.
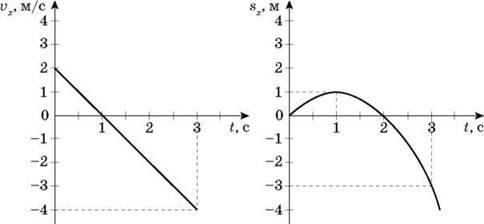
Для побудови графіка l(t) зручніше скористатися не формулою, а вже побудованим графіком sx(t).
Слід урахувати, що при русі в бік, протилежному осі Ох (коли sx < 0), шлях позитивний, причому l = |sx|. Іншими словами, залежність l(t) не є спадаючою. Щоб отримати з графіка sx(t) графік l(t), треба симетрично відобразити відрізок графіка при t > 1 с вгору.
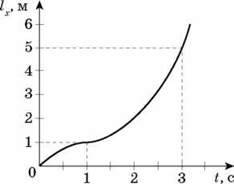
3. На рисунках наведено графіки sx(t) і X(t) для двох різних прямолінійних рухів.
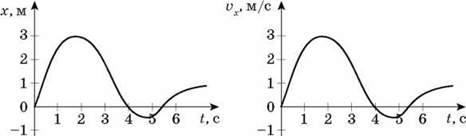
Проаналізуйте графіки, даючи відповіді на наступні запитання:
А) коли тіло рухалося в “негативному” напрямі (протилежному до осі Ох)?
Б) коли швидкість тіла дорівнювала нулю?
В) коли тіло рухалося найшвидше?
Г) коли координата тіла була найменшою?
Д) коли тіло рухалося з максимальним за модулем прискоренням?
Указівка
Тіло 1: а) 1,7 с? t? 4,5 с; б) t = 1,7 с, t = 4,5с, t? 7 с; в) 0,4 с? t? 0,7 с; г) t = 4,5 с; д) t = 1,7 с, t= 4,5 с.
Тіло 2: а) 4 с? t? 5,5 с; б) t = 0, t = 4 с, 5,5 с; в) t = 1,7 с; г) t = 0; д) 0,4 с? t? 0,7 с.
Домашнє завдання
1. П.: §§ 10, 11. 2.
2. 36:
Р1) – 4.4; 4.12; 4.13; 4.14;
Р2) – 4.42; 4.43; 4.44, 4.46;
Р3) – 4.67, 4.68; 4.69; 4. 70, 4.71.
(1 votes, average: 5.00 out of 5)
Loading...